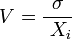об управлении ассортиментом простыми словами
СУТЬ XYZ-АНАЛИЗА
XYZ-анализ – математически-статистический метод, позволяющий анализировать и прогнозировать стабильность продаж отдельных видов товаров и колебания уровня потребления тех или иных товаров. АВС-анализ показывает нам вклад товара в результат магазина, а XYZ анализ показывает стабильность или нестабильность спроса. Чем стабильнее спрос на товар, тем легче мы им управляем, тем ниже потребность в товарных запасах, тем легче планировать движение продукта. Таким образом, мы имеем дополнительный материал для принятия решений о пребывании товара в нашей ассортиментной матрице.
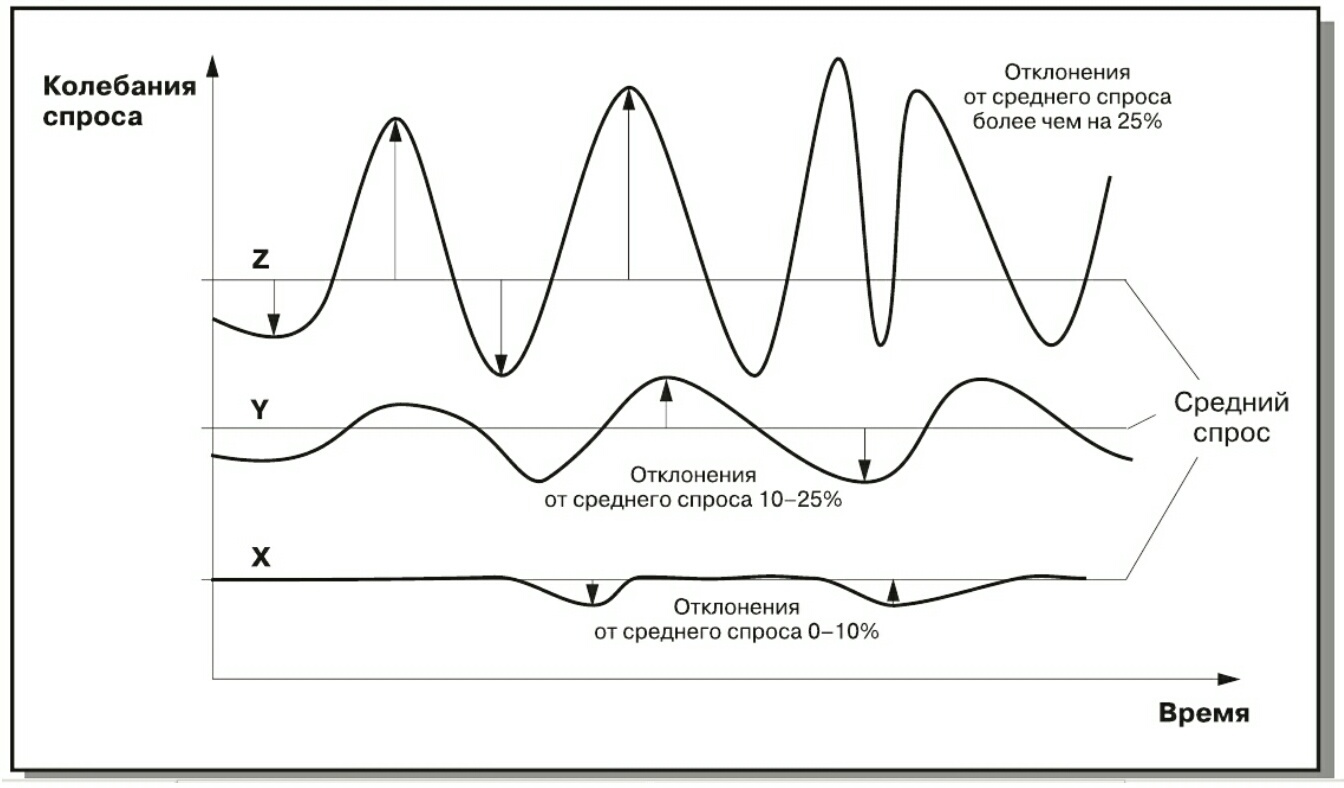
Неделю назад продали 20 батонов хлеба, три дня назад -19 батонов, сегодня – 20, завтра продажи тоже будут равны -19-20 штук. Товар продается стабильно. Это товар Х.
Категория X – есть товары, характеризуются стабильностью продаж и, как следствие, высокими возможностями прогноза продаж Отклонение от средних продаж незначительно (в ту или иную сторону). Отклонение от среднего значения называется КОЭФФИЦИЕНТОМ ВАРИАЦИИ. Для товаров Х
Конфеты: неделю назад продали 20 коробок, три дня назад – 12 коробок, сегодня – 17, завтра продажи будут 23 коробки. Это категория Y – товары, имеющие колебания в спросе и как следствие, средний прогноз продаж. Коэффициент вариации составляет 10% – 25%. Отклонение от средней величины продаж существует, но оно колеблется в разумных пределах – в пределах 25%.
Дорогой элитный коньяк – неделю назад продали 2 бутылки, три дня назад – 0, сегодня пришел человек и купил ящик (наверное, в офис на подарки) – 12 штук, а завтра продажи будут равны 1 бутылке.
Товар нестабилен, относится к категории Z. Категория Z – товары с нерегулярным потреблением, какие-либотенденции отсутствуют, точность прогноза продаж невысокая. Коэффициент вариации превышает 25% и может быть более 100%. Это может быть группа товаров, привозимая по заказу клиентов или недавно поступившая в продажу или товары уникальные, особенные, подверженные сезонному спросу и так далее.
Так же, как и в случае в АВС-анализом, это рекомендованные сочетания, и иногда можно делать допуск коэффициента вариации по группе Х – 0-15%, группе Y – 15-40%, группе Z – от 40%.
ЭТАПЫ XYZ-АНАЛИЗА
1 шаг. Выбираем объект анализа (группа, категория, позиция) и параметр, по которому мы будем сравнивать объекты (продажи за месяц, например). Традиционно в рознице объектами XYZ-анализа являются товарная категория или товарная единица. За основу анализа берется период продаж не менее трех месяцев.
2 шаг. Определить количество периодов, по которым будет проводиться анализ: неделя, декада, месяц, квартал/сезон, полугодие, год. Чем больше период, тем лучше, тем вернее будет статистика спроса. Важно – для анализа надо брать не менее трех периодов, по которым ведется отчетность. Если товар имеет оборачиваемость более месяца, то надо взять период, как минимум в три раза превышающий оборачиваемость (например, оборачиваемость категории «швейные машины» – 2 месяца. Тогда за основу надо взять период не менее 6 – ти месяцев).
3 шаг. Определить коэффициент вариации – среднее квадратическое отклонение – для каждого объекта анализа. Коэффициент вариации означает величину, насколько продажа товара отклоняется от среднестатистической, то есть показывает, стабилен ли спрос на товар или нет.
Расчет коэффициента вариации.
Формула для расчета коэффициента вариации (Кв):
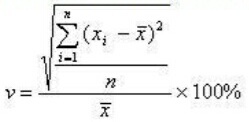
де, хi— значение параметра по оцениваемому объекту за i- тый период,
x — среднее значение параметра по оцениваемому объекту анализа,
п — число периодов
Эта кажущаяся сложной и громоздкой формула легко перекладывается в формулы Excel, с помощью которых применение данного анализа становится очень простым.
Формула Excel выглядит так:
=СТАНДОТКЛОНП(B3:D3)/СРЗНАЧ(B3:D3)
Пример расчета коэффициента вариации по формулам в Excel
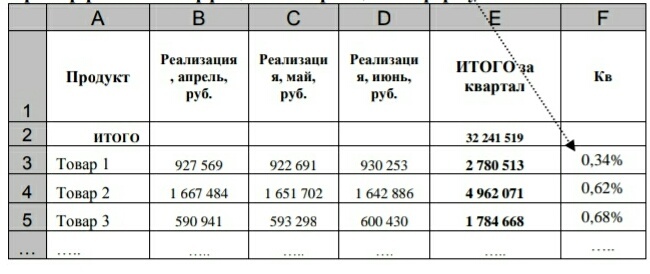
Обратите особое внимание на товары, у которых есть периоды с нулевыми значениями, то есть там, где товар отсутствовал в продаже. Либо исключите их из анализа, либо измените формулу расчета коэффициента вариации – на ноль делить нельзя.
4 шаг. Составить рейтинговый список объектов анализа по возрастанию значения коэффициента вариации. И последнее – определяем, какие объекты относятся к группе X, Y и Z.
Вывод: как видим, некоторые категории пользуются постоянным спросом и по ним можно прогнозировать последующие продажи довольно точно. Однако некоторые категории – «Средства от насекомых», «Бритвенные принадлежности», «Краски для волос» продаются нерегулярно. Стоит внимательнее отнестись к этим категориям – возможно, поставки этих товаров идут с перебоями, или на эти товары проходила акция, которая кратковременно простимулировала спрос. Так же особого внимания требуют товары группы Х – особенно, если их вклад в общий оборот или прибыль невелик. Вероятно, поставки идут фиксированным заказом и товар продается с нулевым остатком до следующей поставки. В таком случае следует дополнительно исследовать спрос на такой товар – возможно, мы недодаем покупателям нужный им товар.
ВАЖНО: если в случае в АВС-анализом у нас всегда будут товары А, В и С, то в случае в XYZ-анализом каких-то товаров может не быть – например, продажи устойчивы и товаров Z нет вообще (что является очень хорошим признаком – значит, можем регулировать величину товарного остатка на основе статистики, спрос постоянный, товар есть на складе). Или хуже: может не быть товаров Х – что говорит о нерегулярном спросе или сбоях в поставках товара.
ОГРАНИЧЕНИЯ XYZ-АНАЛИЗА
В реальной жизни на продажи и доходность товаров в магазине оказывает влияние огромное количество факторов: сезонность спроса, регулярность поставок, колебания цен на аналогичные товары у конкурента,
наличие или отсутствие специальных мероприятий по продвижению и т.д. Все эти факторы будут вызывать колебания продаж, и, как следствие, высокие показатели коэффициента вариации.
Результаты XYZ-анализа будут достоверны, только если анализируется достаточно длительный период времени. Важно, чтобы период, взятый для анализа, в несколько раз превосходил оборачиваемость товара
4 месяца, то для анализа нужно брать период не менее 12 месяцев.
Если же ассортимент обновляется часто, то нужно также использовать информацию о жизненном цикле товара и смотреть тенденцию развития всех новых позиций. Весьма вероятно, что в магазине модной одежды все товары поступают в продажу на один сезон, и тогда в таком магазине у нас вообще не будет группы Х. В случае, если мы имеем дело с сезонными коллекциями одежды и обуви, которые держатся в продаже максимум один сезон, то тогда этот анализ можно проводить по торговым маркам или по поставщикам.
Также важно выяснять причины попадания товара в группу Z: было это вызвано действительно непредсказуемостью спроса, или просто товар нерегулярно попадал в магазин.
XYZ-анализ невозможен, если в ассортименте много новых товаров или поставки идут с перебоями. В таком случае необходимо вводить другой параметр для анализа, а именно запросы или обращения клиентов. Именно ранжирование по обращениям может сделать картину более реальной. Однако и здесь нужно отмечать, идет ли запрос от разных покупателей, или это повторение одного запроса. Поэтому если магазин существует в условиях постоянного дефицита, то этот вид анализа вряд ли покажет истинную картину.
Часто это вид анализа используется в складской логистике, где важно определить частоту спроса для грамотного распределения пространства на складе. В таком случае товары группы Х располагаются в «горячей» зоне отгрузки, товары групп Y и Z – в более отдаленных местах.
Этот анализ очень хорош в сочетании с АВС-анализом – это выявление безусловных лидеров (группы АХ) и аутсайдеров (СZ) в ассортименте магазина.
Что такое коэффициент вариации (CV)
olegas6 месяцев ago / 70 Views
Коэффициент вариации (coefficient of variation, CV) – это статистическая мера дисперсии (разброса) данных вокруг некоторого среднего значения. Коэффициент вариации представляет собой отношение среднеквадратичного отклонения к среднему значению и является весьма полезной величиной для сравнения степени вариации при переходе от одного ряда данных к другому, даже если их средние значения резко отличаются друг от друга.

Понимание коэффициента вариации
Коэффициент вариации показывает степень изменчивости некоторой выборки данных по отношению к среднему их значению. В финансах данный коэффициент позволяет инвесторам определить, насколько велика волатильность, или риск, по сравнению с величиной ожидаемой прибыли от инвестиций.

Чем меньше значение CV, тем лучший компромисс наблюдается между риском и доходностью. Обратите внимание, что если ожидаемая доходность в знаменателе отрицательна или равна нулю, полученное значение коэффициента может ввести вас в заблуждение.
Коэффициент вариации может быть весьма полезен при использовании соотношения риск/прибыль для выбора объекта инвестиций. Например, инвестор не склонный к риску будет рассматривать активы с исторически низкой степенью волатильности и высокой степенью доходности по отношению к общему рынку (или к отдельной отрасли). И наоборот, инвесторы склонные к риску, будут стремиться инвестировать в активы с исторически высокой степенью волатильности.
Формула CV может использоваться для определения дисперсии между исторической средней ценой и текущими показателями цены акции, товара или облигации.
Обычно данный коэффициент используют в таких целях как:
- Для сравнения нескольких различных рядов данных или показателей;
- Для оценки потенциальных объектов инвестирования;
- Для проведения XYZ-анализа.
КЛЮЧЕВЫЕ МОМЕНТЫ
- CV – это статистическая мера дисперсии в ряду данных вокруг среднего значения;
- В финансах CV позволяет инвесторам определить, насколько велика волатильность, или риск, по сравнению с величиной ожидаемой прибыли от инвестиций;
- Чем ниже величина отношения стандартного отклонения к средней доходности,тем лучше соотношение риска и доходности.
Формула CV
Ниже приведена формула для расчета коэффициента вариации:

Обратите внимание, что если значение ожидаемой доходности в знаменателе формулы коэффициента вариации отрицательна или равна нулю, то результат расчёта по ней нельзя считать корректным.
Коэффициент вариации в Excel и Open Office
Коэффициент вариации можно достаточно легко рассчитать в Excel. Несмотря на то, что в нём нет стандартной функции для расчёта CV, но зато есть функции позволяющие рассчитать стандартное отклонение (СТАНДОТКЛОН) и среднее значение (СРЗНАЧ). Сначала используйте функцию стандартного отклонения, затем вычислите среднее значение, а после этого разделите ячейку, содержащую стандартное отклонение, на ячейку содержащую среднее значение.
В Open Office данный показатель рассчитывается аналогично. Функция стандартного отклонения здесь — STDEV, а функция среднего значения — AVERAGE.
Давайте рассмотрим пример расчёта коэффициента вариации в Open Office. Предположим, что у нас есть три потенциальных объекта для инвестиций — объект А, объект Б и объект В. Прибыль по каждому из этих проектов за последние 6 лет занесена в таблицу представленную ниже:

Давайте рассчитаем значение CV для каждого из этих объектов. Начнём с расчёта стандартных отклонений. Для этого применим к ряду значений прибыли отдельно по каждому объекту функцию STDEV:

Аналогичным образом рассчитаем среднее значение для каждого ряда данных:

Наконец рассчитаем CV. Для этого разделим полученные значения отклонений на средние значения. В результате получим следующую таблицу:
 Кликните по картинке для увеличения
Кликните по картинке для увеличенияОчевидно, что из всех представленных объектов инвестиций предпочтительным будет объект Б имеющий наименьшее значение коэффициента CV.
Пример использования коэффициента вариации для выбора объекта инвестиций
Рассмотрим инвестора не склонного к риску, который хочет инвестировать в биржевой фонд (ETF) состоящий из корзины ценных бумаг отслеживающей индекс широкого рынка. Инвестор выбирает SPDR S&P 500 ETF, Invesco QQQ ETF и iShares Russell 2000 ETF. Затем он анализирует доходность и волатильность выбранных ETF за последние 15 лет и предполагает, что в будущем они могут иметь аналогичную доходность в отношении к своим долгосрочным средним значениям.
Для принятия решения инвестором используется следующая 15-летняя историческая информация:
- SPDR S&P 500 ETF имеет среднюю годовую доходность 5,47% и стандартное отклонение 14,68%. Коэффициент вариации SPDR S&P 500 ETF составляет 2,68;
- Средняя годовая доходность Invesco QQQ ETF составляет 6,88%, а стандартное отклонение-21,31%. Коэффициент вариации QQQ равен 3,09;
- iShares Russell 2000 ETF имеет среднюю годовую доходность 7,16% и стандартное отклонение 19,46%. Коэффициент вариации IWM равен 2,72.
Исходя из этих данных, инвестор может инвестировать либо в SPDR S&P 500 ETF, либо в iShares Russell 2000 ETF, так как соотношение риска и вознаграждения для них является сравнительно одинаковым. А для Invesco QQQ ETF соотношение риск-доходность, как видите, будет несколько хуже.
Онлайн калькулятор: Показатели вариации
Пользователь Мария попросила написать такой калькулятор: Показатели вариации и анализ частотных распределений.
Расчеты не очень сложные, поэтому вот и он. Теория, по уже сложившейся традиции, под калькулятором.

Показатели вариации
addimport_exportmode_editdeleteИсследуемая совокупность
Размер страницы: chevron_leftchevron_rightИсследуемая совокупность
Сохранить ОтменитьИмпортировать данныеОшибка импорта
Для разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: -50.5;50
Загрузить данные из csv файла
Импортировать Назад Отменить Точность вычисленияЗнаков после запятой: 2
Среднее арифметическое
Размах вариации
Среднее линейное отклонение
Среднее квадратическое отклонение
Коэффициент осцилляции (проценты)
Относительное линейное отклонение (проценты)
Коэффициент вариации (проценты)
save Сохранить extension Виджет
Вариация — это различие индивидуальных значений какого-либо признака внутри изучаемой совокупности.
Ну, например, есть класс учеников — изучаемая совокупность, у них есть, скажем, годовая оценка по русскому языку. У кого-то она «5», у кого-то «4» ну и так далее. Набор этих оценок по всему классу, вместе с их частотой (т. е. встречаемостью, скажем, у 10 человек – «5», у 7 человек – «4», у 5 человек – «3») и есть вариация, по которой можно рассчитать массу показателей.
Этим мы сейчас и займемся.
Абсолютные показатели
Размах вариации — разность между максимальным и минимальным значениями признака
- Среднее линейное отклонение — среднее арифметическое отклонение индивидуальных значений от средней.
,
где — частота появления значения.
Если индивидуальных значений слишком много, для упрощения расчетов данные могут группировать, т. е. объединять в интервалы. Тогда имеет смысл середины i-го интервала, или среднего значения признака на i-том интервале
- Дисперсия — средняя из квадратов отклонений значений признаков от средней.
Дисперсию также можно рассчитать и таким способом:
, где
- Среднее квадратическое отклонение — , корень из дисперсии.
Относительные показатели
Абсолютные показатели измеряются в тех же величинах, что и сам признак, и показывают абсолютный размер отклонений, поэтому их неудобно применять для сравнения изменчивости разных признаков совокупности. Поэтому дополнительно рассчитывают относительные показатели вариации, которые обычно выражают в в процентах.
Коэффициент осцилляции — характеризует колеблемость крайних значений признака вокруг средней арифметической.
Относительное линейное отклонение или линейный коэффициент вариации — характеризует долю усредненного значения абсолютных отклонений от средней арифметической.
- Коэффициент вариации — характеризует степень однородности совокупности, наиболее часто применяемый показатель.
Совокупность считается однородной при значениях меньше 40%. При значениях больше 40% говорят о большой колеблемости признаков и совокупность считается неоднородной.
Понятие
Коэффициент вариации по 44-ФЗ — это показатель разброса по выбранным ценовым предложениям тендера, применяемый при использовании метода сопоставимых рыночных цен.
Он необходим для определения степени неоднородности полученных цен, так как его значение показывает, какую долю занимает средний разброс от среднего значения.
Коэффициент вариации был введён Приказом Минэкономразвития № 567. Приказ также содержит методические рекомендации по его оптимальным показателям.
Значения
Коэффициент может принимать четыре промежутка, от которых зависит возможность использования исследования рынка:
- менее 10% — разница минимальна;
- от 10 до 20% — средний разброс;
- от 20 до 33% — большой разброс, но допустимый для определения НМЦК;
- свыше 33% — слишком большая разница.
Допустимым вариантом коэффициента вариаций по 44-ФЗ является результат до 33%.
При результате свыше 33% заказчику необходимо сделать новую выборку поставщиков для определения НМЦК.
Использование неоднородных результатов не допускается, а проведённое исследование рынка признаётся недействительным.
В том случае, когда по каким-то причинам запросить другие данные о стоимости на интересующие товары, работы или услуги невозможно, заказчик может воспользоваться сведениями из реестра контрактов.
Расчёт
Коэффициент вариации рассчитывается по формуле:
(Среднеквадратичное отклонение/Средняя стоимость) * 100%
Первая переменная считается следующим образом:
(√∑i=1n (Цена — Средняя арифметическая цена)2)/n — 1, где n — это количество предложений.
При наличии в одной закупке нескольких товаров коэффициент определяется в отношении каждого из них.
От правильного определения коэффициента зависит правильный расчёт НМЦК, поэтому тщательно проверяйте полученные результаты и следите за соответствием допустимым значениям.
( 1 оценка, среднее 5 из 5 )
Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.
Дисперсия
Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.
Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.
Формула дисперсии в теории вероятностей имеет вид:


То есть дисперсия — это математическое ожидание отклонений от математического ожидания.
На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:


где
s2 – выборочная дисперсия, рассчитанная по данным наблюдений,
X – отдельные значения,
X̅– среднее арифметическое по выборке.
Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.
Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
Расчет дисперсии в Excel
Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.


В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).
D(A) = 0
Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
D(AX) = А2 D(X)
Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.
D(A + X) = D(X)
Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.
D(X+Y) = D(X) + D(Y)
Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.
D(X-Y) = D(X) + D(Y)
Среднеквадратичное (стандартное) отклонение
Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:


На практике формула стандартного отклонения следующая:


Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.
Расчет cреднеквадратичного (стандартного) отклонения в Excel
Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).


Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.
Коэффициент вариации
Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:


По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
Расчет коэффициента вариации в Excel
Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:
=СТАНДОТКЛОН.В()/СРЗНАЧ()
Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:


Коэффициент осцилляции
Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.


Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.
Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.
Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.
Поделиться в социальных сетях:
- Коэффициент вариации
Коэффициент вариации случайной величины — мера относительного разброса случайной величины; показывает, какую долю среднего значения этой величины составляет ее средний разброс.
Равен отношению стандартного отклонения к математическому ожиданию.
Так же используется такие обозначение:
 или
или 
Смысл коэффициента
В отличие от среднего квадратического или стандартного отклонения измеряет не абсолютную, а относительную меру разброса значений признака в статистической совокупности. Исчисляется в процентах. Вычисляется только для количественных данных.
Wikimedia Foundation. 2010.
- Дасс, Петтер
- Драгалевский монастырь
Смотреть что такое «Коэффициент вариации» в других словарях:
Коэффициент вариации — мера отклонения опытных данных от выборочного среднего значения, выражаемая в долях единицы или процентах, вычисляется по формуле (5). Источник: ГОСТ 20522 96: Грунты. Методы статистической обработки результатов испытаний … Словарь-справочник терминов нормативно-технической документации
КОЭФФИЦИЕНТ ВАРИАЦИИ — (coefficient of variation) Показатель изменчивости относительно средней величины. Величина измеряется в среднем, а изменчивость измеряется стандартным отклонением, которое равно квадратному корню из среднеквадратичного отклонения от среднего… … Экономический словарь
коэффициент вариации — коэффициент изменчивости — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы коэффициент изменчивости EN coefficient of variation … Справочник технического переводчика
КОЭФФИЦИЕНТ ВАРИАЦИИ — см. Коэффициент изменчивости выборки. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978 … Геологическая энциклопедия
КОЭФФИЦИЕНТ ВАРИАЦИИ — англ. coefficient, variation; нем. Variationskoeffizient. Отнощение стандартного отклонения переменной к ее среднему арифметическому. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
Коэффициент вариации — – относительный показатель однородности прочности и плотности строительного раствора, выраженный в процентах от среднего значения прочности. [ГОСТ 4.233 86] Рубрика термина: Раствор Рубрики энциклопедии: Абразивное оборудование, Абразивы,… … Энциклопедия терминов, определений и пояснений строительных материалов
коэффициент вариации — variacijos koeficientas statusas T sritis Kūno kultūra ir sportas apibrėžtis Vidutinio kvadratinio nuokrypio ir vidurkio santykis; santykinė atsitiktinio dydžio reikšmių nuokrypių nuo jo vidurkio charakteristika. atitikmenys: angl. quotient of… … Sporto terminų žodynas
КОЭФФИЦИЕНТ ВАРИАЦИИ — показатель вариации количественной переменной , измеряющий стандартное отклонение в процентах от среднего арифметического : V = s / x * 100%. Применяется в сравнительном анализе и метанализе для сопоставления результатов, полученных для разных… … Социология: Энциклопедия
КОЭФФИЦИЕНТ ВАРИАЦИИ — См. распределения, коэффициент … Толковый словарь по психологии
КОЭФФИЦИЕНТ ВАРИАЦИИ — англ. coefficient, variation; нем. Variationskoeffizient. Отнощение стандартного отклонения переменной к ее среднему арифметическому … Толковый словарь по социологии
Коэффициент вариации
Из всех показателей вариации среднеквадратическое отклонение в наибольшей степени используется для проведения других видов статистического анализа. Однако среднеквадратическое отклонение дает абсолютную оценку меры разбросанности значений и чтобы понять, насколько она велика относительно самих значений, требуется относительный показатель. Такой показатель называется он коэффициент вариации.
Формула коэффициента вариации:
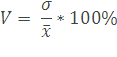
Данный показатель измеряется в процентах (если умножить на 100%).
В статистике принято, что, если коэффициент вариации
меньше 10%, то степень рассеивания данных считается незначительной,
от 10% до 20% — средней,
больше 20% и меньше или равно 33% — значительной,
значение коэффициента вариации не превышает 33%, то совокупность считается однородной,
если больше 33%, то – неоднородной.
Средние, рассчитанные для однородной совокупности – значимы, т.е. действительно характеризуют эту совокупность, для неоднородной совокупности – незначимы, не характеризуют совокупность из-за значительного разброса значений признака в совокупности.
Возьмем пример с расчетом среднего линейного отклонения.

И график для напоминания
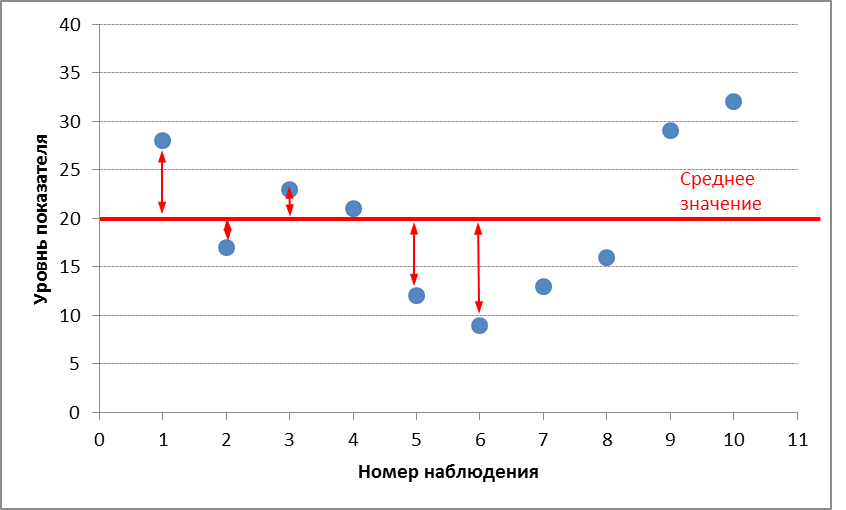
По этим данным рассчитаем: среднее значение, размах вариации, среднее линейное отклонение, дисперсию и стандартное отклонение.
Среднее значение – это обычная средняя арифметическая.
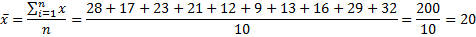
Размах вариации – разница между максимумом и минимумом:
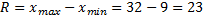
Среднее линейное отклонение считается по формуле:

Дисперсия считается по формуле:
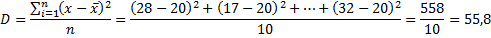
Среднеквадратическое отклонение – квадратный корень из дисперсии:
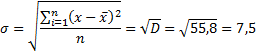
Расчет сведем в табличку.

Вариация показателя отражает изменчивость процесса или явления. Ее степень может измеряться с помощью нескольких показателей.
Размах вариации – разница между максимумом и минимумом. Отражает диапазон возможных значений.
Среднее линейное отклонение – отражает среднее из абсолютных (по модулю) отклонений всех значений анализируемой совокупности от их средней величины.
Дисперсия – средний квадрат отклонений.
Среднеквадратическое отклонение – корень из дисперсии (среднего квадрата отклонений).
Коэффициент вариации – наиболее универсальных показатель, отражающий степень разбросанности значений независимо от их масштаба и единиц измерения. Коэффициент вариации измеряется в процентах и может быть использован для сравнения вариации различных процессов и явлений.
Таким образом, в статистическом анализе существует система показателей, отражающих однородность явлений и устойчивость процессов. Часто показатели вариации не имеют самостоятельного смысла и используются для дальнейшего анализа данных. Исключением является коэффициент вариации, который характеризует однородность данных, что является ценной статистической характеристикой.
7
Автор Маделон Ф. Зади.
Не попадайтесь в ловушку, когда говорите о CV, или не путайте STD с SD. Вы знаете, что они имеют в виду, когда говорят о подлости? Это статистические расчеты хлеба с маслом. Убедитесь, что вы делаете их правильно.
EdD Доцент
Клиническая лаборатория Научная программа Университет Луисвилла
Луисвилл, Кентукки
Июнь 1999
Многие термины, описанные в этом уроке, также содержатся в уроках по основным практикам контроля качества, которые представлены на этом веб-сайте.Настоятельно рекомендуется изучать эти уроки онлайн или в печатном виде [1]. Важность этого текущего урока, однако, заключается в этом процессе. Урок устанавливает образец, которому нужно следовать в будущих уроках.
Среднее или среднее
Простейшая статистика — это среднее или среднее. Несколько лет назад, когда лаборатории начали анализировать контроли, было легко вычислить среднее значение и использовать это значение в качестве «цели», которую нужно достичь. Например, учитывая следующие десять анализов контрольного материала — 90, 91, 89, 84, 88, 93, 80, 90, 85, 87 — среднее значение или Xbar составляет 877/10 или 87.7. [Термин Xbar относится к символу, имеющему линию или черту над X, 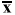 , однако мы будем использовать термин вместо символа в тексте этих уроков, поскольку его легче представить.]
, однако мы будем использовать термин вместо символа в тексте этих уроков, поскольку его легче представить.]
Среднее значение характеризует «центральную тенденцию» или «местоположение» данных. Хотя среднее значение является наиболее вероятным значением, многие фактические значения отличаются от среднего. При анализе контрольных материалов очевидно, что технологи не будут получать среднее значение каждый раз, когда анализ анализируется.Наблюдаемые значения показывают дисперсию или распределение относительно среднего значения, и это распределение необходимо охарактеризовать, чтобы установить диапазон приемлемых контрольных значений.
Стандартное отклонение
Дисперсия значений относительно среднего является предсказуемой и может быть охарактеризована математически с помощью ряда манипуляций, как показано ниже, где отдельные значения x показаны в столбце A.
| Колонна A | Колонна B | Колонна C |
| X значение | X value-Xbar | (X-Xbar) 2 |
| 90 | 90 — 87.7 = 2,30 | (2,30) 2 = 5,29 |
| 91 | 91 — 87,7 = 3,30 | (3,30) 2 = 10,89 |
| 89 | 89 — 87,7 = 1,30 | (1,30) 2 = 1,69 |
| 84 | 84 — 87,7 = -3,70 | (-3,70) 2 = 13,69 |
| 88 | 88 — 87.7 = 0,30 | (0,30) 2 = 0,09 |
| 93 | 93 — 87,7 = 5,30 | (5,30) 2 = 28,09 |
| 80 | 80 — 87,7 = -7,70 | (-7,70) 2 = 59,29 |
| 90 | 90 — 87,7 = 2,30 | (2,30) 2 = 5,29 |
| 85 | 85 — 87.7 = -2,70 | (-2,70) 2 = 7,29 |
| 87 | 87 — 87,7 = -0,70 | (-0,70) 2 = 0,49 |
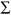 X = 877 X = 877 | 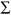 (X-Xbar) = 0 (X-Xbar) = 0 | 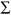 (X-Xbar) ² = 132,10 (X-Xbar) ² = 132,10 |
- Первой математической манипуляцией является суммирование (
 ) отдельных точек и вычисление среднего или среднего значения, которое равно 877, деленному на 10 или 87.7 в этом примере.
) отдельных точек и вычисление среднего или среднего значения, которое равно 877, деленному на 10 или 87.7 в этом примере. - Вторая манипуляция состоит в том, чтобы вычесть среднее значение из каждого контрольного значения, как показано в столбце B. Этот термин, обозначенный как значение X — Xbar, называется оценкой разности. Как можно видеть здесь, отдельные оценки различий могут быть положительными или отрицательными, и сумма оценок различий всегда равна нулю.
- Третья манипуляция заключается в возведении в квадрат разницы, чтобы сделать все члены положительными, как показано в столбце С.
- Следующие квадраты разностей суммируются.
- Наконец, предсказуемую дисперсию или стандартное отклонение (SD или s) можно рассчитать следующим образом:
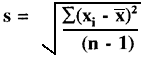
= [132,10 / (10-1)] 1/2 = 3,83
Степени свободы
Термин «n-1» в вышеприведенном выражении представляет степеней свободы (df). Сильно истолкованный, термин «степени свободы» указывает, сколько свободы или независимости существует в группе чисел. Например, если вы хотите сложить четыре числа, чтобы получить общее количество, у вас есть свобода выбора любых чисел, которые вам нравятся.Однако, если сумма четырех чисел установлена равной 92, выбор первых 3 чисел является достаточно свободным (если они являются младшими числами), но последний выбор ограничен условием, что сумма должна равняться 92 Например, если первые три числа, выбранные случайным образом, равны 28, 18 и 36, эти числа составляют в сумме 82, что на 10 меньше цели. Для последнего номера нет свободы выбора. Число 10 должно быть выбрано, чтобы сумма получилась равной 92. Следовательно, степени свободы были ограничены 1, и остались только n-1 степеней свободы.В формуле SD степени свободы n минус 1, поскольку среднее значение данных уже рассчитано (что накладывает одно условие или ограничение на набор данных).
дисперсия
Другим статистическим термином, связанным с распределением, является дисперсия, которая является квадратом стандартного отклонения (дисперсия = SD²). SD может иметь положительное или отрицательное значение, поскольку рассчитывается как квадратный корень, который может быть как положительным, так и отрицательным. Возводя в квадрат SD, проблема знаков устранена.Одним из распространенных применений дисперсии является ее использование в F-тесте для сравнения дисперсии двух методов и определения наличия статистически значимой разницы в неточности между методами.
Однако во многих приложениях SD часто является предпочтительным, поскольку она выражается в тех же единицах концентрации, что и данные. Используя SD, можно предсказать диапазон контрольных значений, которые следует соблюдать, если метод остается стабильным. Как обсуждалось в предыдущем уроке, лаборанты часто используют SD для наложения «ворот» на ожидаемое нормальное распределение контрольных значений.
Нормальное или гауссово распределение
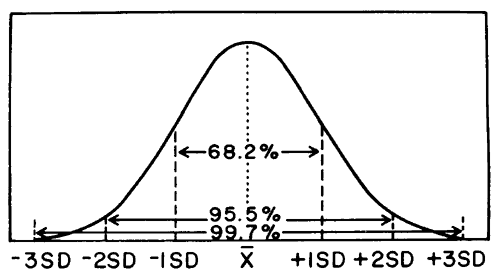 Традиционно, после обсуждения среднего значения, стандартного отклонения, степеней свободы и дисперсии, следующим шагом было описание нормального распределения (многоугольника частоты) в терминах «ворот» стандартного отклонения. Рисунок здесь представляет собой распределение частот большого набора лабораторных значений, полученных путем измерения одного контрольного материала. Это распределение показывает форму нормальной кривой. Обратите внимание, что «ворота», состоящие из ± 1SD, составляют 68% распределения или 68% площади под кривой, ± 2SD — 95%, а ± 3SD -> 99%.При ± 2SD 95% распределения находится внутри «ворот», 2,5% распределения находится в нижнем или левом хвосте, и такое же количество (2,5%) присутствует в верхнем хвосте. Некоторые авторы называют этот многоугольник кривой ошибок, чтобы проиллюстрировать, что маленькие средние ошибки встречаются чаще, чем большие. Другие авторы называют эту кривую распределением вероятностей.
Традиционно, после обсуждения среднего значения, стандартного отклонения, степеней свободы и дисперсии, следующим шагом было описание нормального распределения (многоугольника частоты) в терминах «ворот» стандартного отклонения. Рисунок здесь представляет собой распределение частот большого набора лабораторных значений, полученных путем измерения одного контрольного материала. Это распределение показывает форму нормальной кривой. Обратите внимание, что «ворота», состоящие из ± 1SD, составляют 68% распределения или 68% площади под кривой, ± 2SD — 95%, а ± 3SD -> 99%.При ± 2SD 95% распределения находится внутри «ворот», 2,5% распределения находится в нижнем или левом хвосте, и такое же количество (2,5%) присутствует в верхнем хвосте. Некоторые авторы называют этот многоугольник кривой ошибок, чтобы проиллюстрировать, что маленькие средние ошибки встречаются чаще, чем большие. Другие авторы называют эту кривую распределением вероятностей.
Коэффициент вариации
Другой способ описать вариацию теста — это вычислить коэффициент вариации или CV.CV выражает отклонение в процентах от среднего и рассчитывается следующим образом:
CV% = (SD / Xbar) 100
В лаборатории CV предпочтительнее, когда SD увеличивается пропорционально концентрации. Например, данные из эксперимента по репликации могут показать SD 4 единиц в концентрации 100 единиц и SD 8 единиц в концентрации 200 единиц. CV составляют 4,0% на обоих уровнях, и CV более полезен, чем SD, для описания эффективности метода при концентрациях между ними.Однако не все тесты продемонстрируют неточность, которая является постоянной с точки зрения CV. Для некоторых тестов SD может быть постоянным во всем аналитическом диапазоне.
Резюме также дает общее «представление» о производительности метода. Резюме 5% или менее обычно дают нам ощущение хорошей производительности метода, тогда как резюме 10% и выше звучат плохо. Тем не менее, вы должны внимательно посмотреть на среднее значение, прежде чем судить о резюме. При очень низких концентрациях CV может быть высоким, а при высоких концентрациях CV может быть низким.Например, тест на билирубин с SD 0,1 мг / дл при среднем значении 0,5 мг / дл имеет CV 20%, тогда как SD 1,0 мг / дл при концентрации 20 мг / дл соответствует CV 5,0%.
Альтернативные формулы
Уроки по базовым практикам контроля качества охватывают эти же термины (см. Контроль качества — Расчеты данных), но используют другую форму уравнения для расчета кумулятивных или актуальных средних и SD. Руководства в литературе рекомендуют использовать кумулятивные средние значения и СО для расчета контрольных пределов [2-4], поэтому важно иметь возможность выполнять эти вычисления.
Совокупное среднее значение может быть выражено как Xbar = (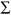 x i ) t / n t , что выглядит аналогично предыдущему среднему термину, за исключением индексов «t», которые относятся к данным за разные периоды времени , Идея состоит в том, чтобы добавить
x i ) t / n t , что выглядит аналогично предыдущему среднему термину, за исключением индексов «t», которые относятся к данным за разные периоды времени , Идея состоит в том, чтобы добавить 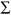 x i и n членов из групп данных, чтобы вычислить среднее значение для объединенных групп.
x i и n членов из групп данных, чтобы вычислить среднее значение для объединенных групп.
Накопленное или стандартное отклонение по дате может быть выражено следующим образом:
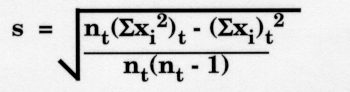
Это уравнение выглядит совсем не так, как в предыдущем уроке, но в действительности оно эквивалентно.Формула кумулятивного стандартного отклонения получена из формулы SD, называемой формулой необработанного балла. Вместо того, чтобы сначала вычислять среднее значение или Xbar, необработанный счет Формула вычисляет Xbar внутри знака квадратного корня.
Часто, читая о статистике, может быть представлена незнакомая формула. Вы должны понимать, что математика в статистике часто избыточна. Каждая процедура основана на предыдущей процедуре. Формулы, которые кажутся различными, получены из математических манипуляций со стандартными выражениями, с которыми вы часто уже знакомы.
Рекомендации
- Westgard JO, Barry, PL, Quam EF. Основные практики контроля качества: Обучение статистическому контролю качества для медицинских лабораторий. Madison, WI: Westgard Quality Corporation, 1998.
- Вестгард Дж.О., Барри П.Л., Хант М.Р., Грот Т. Многопрофильная диаграмма Шухарта для контроля качества в клинической химии. Clin Chem 1981; 27: 493-501.
- Westgard JO, Klee GG. Управление качеством. Глава 17 в Tietz Учебник клинической химии, 3-е изд., Буртис и Эшвуд, ред. Филадельфия, Пенсильвания: Сондерс, 1999.
- NCCLS C24-A2 документ. Статистический контроль качества для количественных измерений: принципы и определения. Национальный комитет по клиническим лабораторным стандартам, Уэйн П.А., 1999.
Упражнения для самооценки
- Рассчитайте вручную среднее значение, SD и CV для следующих данных: 44, 47, 48, 43, 48.
- Используйте калькулятор SD для расчета среднего значения, SD и CV для следующих данных: 203, 202, 204, 201, 197, 200, 198, 196, 206, 198, 196, 192, 205, 190, 207, 198 201, 195, 209, 186.
- Если вышеприведенные данные относятся к контрольному материалу на холестерин, рассчитайте контрольные пределы, которые будут содержать 95% ожидаемых значений.
- Если контрольные пределы (или «ворота» SD) были установлены как среднее значение +/- 2,5 SD, какой процент контрольных значений должен превышать эти пределы? [Подсказка: вам нужно найти таблицу областей под нормальной кривой.]
- Опишите, как рассчитать совокупные контрольные пределы.
- (Необязательно) Показать эквивалентность обычной формулы SD и формулы необработанного балла.[Подсказка: начните с обычной формулы, замените сумму суммирования на Xbar, умножьте обе стороны на n / n, затем переставьте.]
Об авторе: Маделон Ф. Зади
Маделон Ф. Зади является доцентом в Университете Луисвилля, Школе наук о клинических лабораториях по естественным наукам, и имеет более 30 лет опыта преподавания. Она имеет степень бакалавра, магистра и доктора наук в Университете Луисвилля, взяла другую продвинутую курсовую работу в Школе медицины и Школе образования, а также продвинутые курсы в области статистики.Она является зарегистрированным MT (ASCP) и имеет сертификат CLS (NCA) и 14 лет проработала в качестве технолога на стенде. Она является членом: Американского общества клинических лабораторных исследований, Государственного общества клинических лабораторных исследований штата Кентукки, Американской ассоциации образовательных исследований и Национальной ассоциации преподавателей естественных наук. Области преподавания: клиническая химия и статистика. Область ее исследований — метакогнитивная теория и теория обучения.
- Образование
- Математика
- Бизнес-статистика
- Проверка оценочного уравнения регрессии с использованием коэффициента определения, R 2
Алан Андерсон
После оценки линии регрессии населения можно проверить, имеет ли смысл уравнение регрессии, используя коэффициент детерминации, также известный как R 2 ( R в квадрате).Это используется как мера того, насколько хорошо уравнение регрессии фактически описывает взаимосвязь между зависимой переменной ( Y ) и независимой переменной ( X ).
Может случиться так, что между зависимыми и независимыми переменными нет реальной связи; простая регрессия дает результаты, даже если это так. Поэтому важно подвергнуть результаты регрессии некоторым ключевым тестам, которые позволят вам определить, являются ли результаты надежными.
Коэффициент детерминации, R 2 , является статистической мерой, которая показывает долю вариации , объясняемой оценочной линией регрессии. Отклонение относится к сумме квадратов разностей между значениями Y и средним значением Y , математически выраженных как
R 2 всегда принимает значение от 0 до 1. Чем ближе R 2 к 1, тем лучше расчетное уравнение регрессии соответствует или объясняет связь между X и Y .
Выражение
также известен как общая сумма квадратов (TSS).
Эта сумма может быть разделена на следующие две категории:
Объясненная сумма квадратов (ESS): Также известный как объясненная вариация , ESS является частью полной вариации, которая измеряет, насколько хорошо уравнение регрессии объясняет связь между X и Y .
Вы вычисляете ESS по формуле
Остаточная сумма квадратов (RSS): Это выражение также известно как необъяснимое изменение и является частью общего отклонения, которое измеряет расхождения (ошибки) между фактическими значениями Y и теми, которые оцениваются с помощью уравнения регрессии.
Вы рассчитываете RSS по формуле
Чем меньше значение RSS относительно ESS, тем лучше линия регрессии соответствует или объясняет связь между зависимой и независимой переменной.
Общая сумма квадратов (TSS):
Сумма RSS и ESS равна TSS.
R 2 — это отношение объясненной суммы квадратов (ESS) к общей сумме квадратов (TSS):
Вы также можете использовать эту формулу:
На основании определения R 2 его значение никогда не может быть отрицательным.Кроме того, R 2 не может быть больше 1, поэтому
При простом регрессионном анализе R 2 равно квадрату корреляции между X и Y .
Коэффициент детерминации используется как мера того, насколько хорошо линия регрессии объясняет взаимосвязь между зависимой переменной ( Y ) и независимой переменной ( X ). Чем ближе коэффициент детерминации к 1, тем ближе линия регрессии соответствует данным выборки.
Коэффициент детерминации вычисляется из сумм квадратов. Эти расчеты сведены в следующую таблицу.
Чтобы вычислить ESS, вычтите среднее значение Y из каждого из расчетных значений Y ; каждый член возводится в квадрат, а затем складывается вместе:
Чтобы вычислить RSS, вычтите расчетное значение Y из каждого фактического значения Y ; каждый член возводится в квадрат, а затем складывается вместе:
Чтобы вычислить TSS, вычтите среднее значение Y из каждого фактического значения Y ; каждый член возводится в квадрат, а затем складывается вместе:
Кроме того, вы можете просто добавить ESS и RSS для получения TSS:
TSS = ESS + RSS = 0.54 + 0,14 = 0,68
Коэффициент детерминации ( R 2 ) — это отношение ESS к TSS:
Это показывает, что 79,41% вариации Y объясняется вариацией X . Поскольку коэффициент детерминации не может превышать 100 процентов, значение 79,41 указывает, что линия регрессии близко соответствует фактическим данным выборки.
Об авторе книги
Алан Андерсон , доктор философии, преподаватель финансов, экономики, статистики и математики в университетах Фордхэм и Фэрфилд, а также в колледжах Манхэттенвилля и Закупки.Вне академической среды он имеет многолетний опыт работы экономистом, риск-менеджером и аналитиком с фиксированным доходом. Алан получил степень доктора экономических наук в Университете Фордхэма и степень магистра наук. в области финансового инжиниринга из Политехнического университета.
,Для объяснения и повседневных примеров использования процентов обычно смотрите нашу страницу Проценты: Введение . Для более общих процентных расчетов см. Нашу страницу Процентные калькуляторы .
Для расчета процентного увеличения:
Первое: вычислите разницу (увеличение) между двумя числами, которые вы сравниваете.
Увеличение = Новый номер — Оригинальный номер
Затем: разделите увеличение на исходное число и умножьте ответ на 100.
% увеличение = увеличение ÷ оригинальный номер × 100 .
Если ваш ответ отрицательный, то это процентное уменьшение.
Чтобы рассчитать процентное уменьшение:
Первое: вычислите разницу (уменьшение) между двумя числами, которые вы сравниваете.
Уменьшение = Оригинальный номер — Новый номер
Затем: разделите уменьшение на исходное число и умножьте ответ на 100.
% Уменьшение = Уменьшение ÷ Оригинальный номер × 100
Если ваш ответ отрицательный, то это процентное увеличение.
Если вы хотите рассчитать процентное увеличение или уменьшение нескольких чисел, мы рекомендуем использовать первую формулу. Положительные значения указывают на процентное увеличение, тогда как отрицательные значения указывают на процентное уменьшение.

Калькулятор процентного изменения
Используйте этот калькулятор для расчета процентного изменения двух чисел
Подробнее: Процентные калькуляторы
Примеры — процентное увеличение и уменьшение
В январе Дилан работал в общей сложности 35 часов, в феврале он работал 45.5 часов — на сколько процентов увеличилось рабочее время Дилана в феврале?
Для решения этой проблемы сначала рассчитаем разницу в часах между новым и старым числами. 45,5 — 35 часов = 10,5 часов. Мы видим, что Дилан работал в феврале на 10,5 часов больше, чем в январе — это его увеличение на и на . Чтобы рассчитать увеличение в процентах, теперь необходимо разделить увеличение на исходное (январьское) число:
10,5 ÷ 35 = 0.3 (см. Нашу страницу , раздел для получения инструкций и примеров деления.)
Наконец, чтобы получить процент, мы умножаем ответ на 100. Это просто означает перемещение десятичного знака на два столбца вправо.
0,3 × 100 = 30
Дилан поэтому работал в феврале на 30% больше часов, чем в январе.
В марте Дилан снова работал 35 часов — так же, как в январе (или 100% его январских часов). Какая процентная разница между февральскими часами Дилана (45.5) а его мартовские часы (35)?
Сначала вычислите уменьшение в часах, то есть: 45,5 — 35 = 10,5
Затем разделите уменьшение на исходное число (февральские часы) так:
10,5 ÷ 45,5 = 0,23 (до двух десятичных знаков).
Наконец, умножьте 0,23 на 100, чтобы получить 23%. Часы Дилана в марте были на 23% ниже, чем в феврале.
Возможно, вы подумали, потому что между январскими часами Дилана (35) и февралем (45) произошло увеличение на 30%.5) часы, что также будет на 30% меньше между его февральскими и мартовскими часами. Как видите, это предположение неверно.
Причина в том, что наше исходное число отличается в каждом случае (35 в первом примере и 45,5 во втором). Это подчеркивает, насколько важно убедиться, что вы рассчитываете процент от правильной начальной точки.
Иногда легче показать процентное уменьшение как отрицательное число — для этого следуйте приведенной выше формуле для расчета процентного увеличения — ваш ответ будет отрицательным числом, если произошло уменьшение.В случае Дилана увеличение часов в период с февраля по март составляет -10,5 (отрицательный, потому что это уменьшение). Поэтому -10,5 ÷ 45,5 = -0,23. -0,23 × 100 = -23%.
Часы Дилана могут быть отображены в таблице данных как:
| месяц | часов отработано | Процент Изменение |
| январь | 35 | |
| февраля | 45.5 | 30% |
| март | 35 | -23% |
Расчет значений на основе процентного изменения
Иногда полезно иметь возможность рассчитывать фактические значения на основе процентного увеличения или уменьшения. Распространено видеть примеры того, когда это может быть полезно в СМИ.
Вы можете увидеть заголовки как:
В Великобритании количество осадков было этим летом на 23% выше среднего.
Показатели безработицы показывают снижение на 2%.
Банкиры ‘бонусы сократились на 45%.
Эти заголовки дают представление о тенденции — когда что-то увеличивается или уменьшается, но зачастую нет фактических данных.
Без данных цифры процентного изменения могут вводить в заблуждение.
В графстве Середигион в Западном Уэльсе очень низкий уровень насильственных преступлений.
Полицейские отчеты для Ceredigion в 2011 году показали 100% увеличение числа насильственных преступлений. Это поразительное число, особенно для тех, кто живет или думает о переезде в Ceredigion.
Однако, когда исходные данные изучаются, это показывает, что в 2010 году в Ceredigion было зарегистрировано одно насильственное преступление. Таким образом, увеличение на 100% в 2011 году означало, что было зарегистрировано два насильственных преступления.
Когда сталкиваются с фактическими цифрами, восприятие количества насильственных преступлений в Ceredigion значительно меняется.
Чтобы понять, насколько что-то увеличилось или уменьшилось в реальном выражении, нам нужны реальные данные.
Возьмем пример « осадков в Великобритании этим летом было на 23% выше среднего уровня » — мы можем сразу сказать, что в Великобритании выпало почти на четверть (25%) больше осадков, чем в среднем за лето.Тем не менее, не зная, каково среднее количество осадков или сколько осадков выпало за рассматриваемый период, мы не можем определить, сколько осадков выпало на самом деле.
Расчет фактического количества осадков за период, если известно среднее количество осадков.
Если мы знаем, что среднее количество осадков составляет 250 мм, мы можем рассчитать количество осадков за период путем расчета 250 + 23%.
Первая тренировка 1% из 250, 250 ÷ 100 = 2,5. Затем умножьте ответ на 23, потому что количество осадков увеличилось на 23%.
2,5 × 23 = 57,5.
Общее количество осадков за рассматриваемый период составило 250 + 57,5 = 307,5 мм.
Расчет среднего количества осадков, если фактическое количество известно.
Если в сообщении новостей говорится о новом измерении и процентном увеличении, « осадков в Великобритании были на 23% выше среднего … 320 мм осадков выпало… ».
В этом примере мы знаем, что общее количество осадков составило 320 мм. Мы также знаем, что это на 23% выше среднего. Другими словами, 320 мм соответствует 123% (или 1.23 раза) среднего количества осадков. Чтобы вычислить среднее значение, мы разделим сумму (320) на 1,23.
320 ÷ 1,23 = 260,1626. Округлено до одного знака после запятой, среднее количество осадков составляет 260,2 мм .
Теперь можно рассчитать разницу между средним и фактическим количеством осадков:
320 — 260,2 = 59,8 мм .
Мы можем сделать вывод, что 59,8 мм — это 23% от среднего количества осадков (260,2 мм), и что в реальном выражении выпало на 59,8 мм больше осадков, чем в среднем.
Мы надеемся, что вы нашли эту страницу полезной — почему бы не проверить наши другие страницы навыков счета? Или сообщите нам о предмете, который вы хотели бы видеть на SkillsYouNeed — Свяжитесь с нами .
, График нормального распределения (или кривая колокола). Каждая цветная полоса имеет ширину одного стандартного отклонения.
График нормального распределения (или кривая колокола). Каждая цветная полоса имеет ширину одного стандартного отклонения. 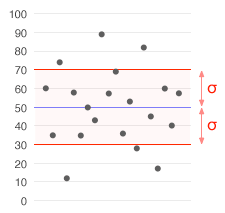
Набор данных со средним значением 50 (показан синим цветом) и стандартным отклонением (σ) 20.
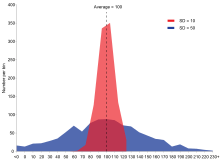 Пример двух выборочных популяций с одинаковым средним и разными стандартными отклонениями. Красная популяция имеет среднее значение 100 и SD 10; синяя популяция имеет среднее значение 100 и SD 50.
Пример двух выборочных популяций с одинаковым средним и разными стандартными отклонениями. Красная популяция имеет среднее значение 100 и SD 10; синяя популяция имеет среднее значение 100 и SD 50.Стандартное отклонение — это число, используемое для определения того, как измерения для группы разбросаны по среднему (среднему) или ожидаемому значению.Низкое стандартное отклонение означает, что большинство чисел близко к среднему. Высокое стандартное отклонение означает, что числа более разбросаны. [1] [2]
Сообщаемая погрешность обычно вдвое больше стандартного отклонения. Ученые обычно сообщают о стандартном отклонении чисел от среднего числа в экспериментах. Они часто решают, что важны только различия, превышающие стандартное отклонение более чем в два или три раза. Стандартное отклонение также полезно в деньгах, где стандартное отклонение на заработанные проценты показывает, насколько могут отличаться заработанные проценты одного человека от среднего.
Много раз можно измерить только образец или часть группы. Затем число, близкое к стандартному отклонению для всей группы, можно найти с помощью немного другого уравнения, называемого стандартным отклонением выборки, которое поясняется ниже.
Рассмотрим группу, имеющую следующие восемь чисел:
- 2 , 4 , 4 , 4 , 5 , 5 , 7 , 9 {\ displaystyle 2, \ 4, \ 4, \ 4, \ 5, \ 5, \ 7, \ 9}
Эти восемь чисел имеют среднее (среднее) 5:
- 2 + 4 + 4 + 4 + 5 + 5 + 7 + 9 8 знак равно 5 {\ displaystyle {\ frac {2 + 4 + 4 + 4 + 5 + 5 + 7 + 9} {8}} = 5}
Чтобы рассчитать стандартное отклонение популяции, сначала найдите разницу каждого числа в списке от среднего значения.Затем возведите в квадрат результат каждой разницы:
- ( 2 — 5 ) 2 знак равно ( — 3 ) 2 знак равно 9 ( 5 — 5 ) 2 знак равно 0 2 знак равно 0 ( 4 — 5 ) 2 знак равно ( — 1 ) 2 знак равно 1 ( 5 — 5 ) 2 знак равно 0 2 знак равно 0 ( 4 — 5 ) 2 знак равно ( — 1 ) 2 знак равно 1 ( 7 — 5 ) 2 знак равно 2 2 знак равно 4 ( 4 — 5 ) 2 знак равно ( — 1 ) 2 знак равно 1 ( 9 — 5 ) 2 знак равно 4 2 знак равно 16 {\ displaystyle {\ begin {array} {lll} (2-5) ^ {2} = (- 3) ^ {2} = 9 && (5-5) ^ {2} = 0 ^ {2} = 0 \ \ (4-5) ^ {2} = (- 1) ^ {2} = 1 && (5-5) ^ {2} = 0 ^ {2} = 0 \\ (4-5) ^ {2} = (-1) ^ {2} = 1 && (7-5) ^ {2} = 2 ^ {2} = 4 \\ (4-5) ^ {2} = (- 1) ^ {2} = 1 && ( 9-5) ^ {2} = 4 ^ {2} = 16 {\\\ конец массива}}}
Далее найдите среднее из этих значений (сумма, деленная на количество чисел).Наконец, возьмите квадратный корень:
- ( 9 + 1 + 1 + 1 + 0 + 0 + 4 + 16 ) 8 знак равно 2 {\ displaystyle {\ sqrt {\ frac {(9 + 1 + 1 + 1 + 0 + 0 + 4 + 16)} {8}}} = 2}
Ответ — стандартное отклонение населения .Формула верна, только если восемь чисел, с которых мы начали, являются целой группой. Если они являются только частью группы, выбранной случайным образом, то мы должны использовать 7 (что составляет n — 1) вместо 8 (что составляет n ) в нижней части (знаменатель) второго по последнему слову шаг. Тогда ответом является стандартное отклонение . Это называется исправлением Бесселя.
Пример чуть сложнее, из реальной жизни: средний рост для взрослых мужчин в Соединенных Штатах — 70 «, со стандартным отклонением 3».Стандартное отклонение 3 «означает, что большинство мужчин (около 68%, при условии нормального распределения) имеют рост на 3» выше на 3 «ниже среднего (67» -73 «) — одно стандартное отклонение. Почти все мужчины (около 95%) имеют рост от 6 «выше до 6» короче среднего (64 «-76») — два стандартных отклонения. Три стандартных отклонения включают все числа для 99,7% исследуемой популяции. Это верно, если Распределение нормальное (колоколообразное).
Если бы стандартное отклонение было равно нулю, тогда все люди были бы ровно 70 «ростом.Если бы стандартное отклонение было 20 «, то некоторые мужчины были бы намного выше или намного ниже среднего, с типичным диапазоном около 50» -90 «.
Для другого примера, каждая из трех групп {0, 0, 14, 14}, {0, 6, 8, 14} и {6, 6, 8, 8} имеет среднее (среднее) значение 7. Но их стандартные отклонения равны 7, 5 и 1. Третья группа имеет гораздо меньшее стандартное отклонение, чем две другие, потому что все ее числа близки к 7. Основная идея заключается в том, что стандартное отклонение говорит нам, как далеко от среднего значения остальные из числа, как правило,У него будут те же единицы, что и у самих чисел. Например, если группа {0, 6, 8, 14} — это возраст группы из четырех братьев по годам, среднее значение составляет 7 лет, а стандартное отклонение — 5 лет.
Стандартное отклонение может служить мерой неопределенности. Например, в науке стандартное отклонение группы повторных измерений помогает ученым узнать, насколько они достоверны по среднему числу. При принятии решения о том, согласуются ли измерения из эксперимента с прогнозом, стандартное отклонение этих измерений очень важно.Если среднее число из экспериментов слишком далеко от предсказанного числа (с расстоянием, измеренным в стандартных отклонениях), то проверяемая теория может быть не верной. Смотрите интервал прогнозирования.
Примеры применения [изменить | изменить источник]
Использование понимания стандартного отклонения набора значений заключается в том, чтобы узнать, насколько велика разница от «среднего» (среднего).
Погода [изменить | изменить источник]
В качестве простого примера рассмотрим среднесуточные высокие температуры для двух городов, одного внутри страны и одного у океана.Полезно понимать, что диапазон суточных высоких температур для городов, расположенных около океана, меньше, чем для городов внутри страны. Эти два города могут иметь одинаковую среднесуточную высокую температуру. Однако стандартное отклонение дневной высокой температуры для прибрежного города будет меньше, чем для внутреннего города.
Спорт [изменить | изменить источник]
Другой способ увидеть это — рассмотреть спортивные команды. В любом виде спорта будут команды, которые хороши в одних вещах, а не в других.Команды, занявшие наивысшие оценки, не будут сильно отличаться друг от друга. Они преуспевают в большинстве категорий. Чем ниже стандартное отклонение их способностей в каждой категории, тем более сбалансированными и последовательными они являются. Команды с более высоким стандартным отклонением, однако, будут менее предсказуемыми. Команда, которая обычно плоха в большинстве категорий, будет иметь низкое стандартное отклонение. Команда, которая обычно хороша в большинстве категорий, также будет иметь низкое стандартное отклонение. Тем не менее, команда с высоким стандартным отклонением может быть той командой, которая набирает много очков (сильное нарушение), но также позволяет другой команде набрать много очков (слабая защита).
Попытка узнать заранее, какие команды выиграют, может включать рассмотрение стандартных отклонений «статистики» различных команд. Числа, которые отличаются от ожидаемых, могут соответствовать сильным и слабым сторонам, чтобы показать, какие причины могут быть наиболее важными в знании, какая команда победит.
В гонках измеряется время, которое требуется водителю, чтобы закончить каждый круг по трассе. Водитель с низким стандартным отклонением времени круга более последовательный, чем водитель с более высоким стандартным отклонением.Эта информация может использоваться, чтобы помочь понять, как водитель может сократить время, чтобы закончить круг.
Деньги [изменить | изменить источник]
В деньгах стандартное отклонение может означать риск того, что цена будет расти или падать (акции, облигации, имущество и т. Д.). Это также может означать риск того, что группа цен будет расти или уменьшаться [3] (активно управляемые взаимные фонды, индексные взаимные фонды или ETF). Риск является одной из причин для принятия решения о том, что купить. Риск — это число, которое люди могут использовать, чтобы узнать, сколько денег они могут заработать или потерять.По мере того как риск возрастает, отдача от инвестиций может оказаться больше ожидаемой (стандартное отклонение «плюс»). Однако инвестиции могут также потерять больше денег, чем ожидалось (стандартное отклонение «минус»).
Например, человеку пришлось выбирать между двумя акциями. Акции за последние 20 лет имели среднюю доходность 10 процентов со стандартным отклонением 20 процентных пунктов (п.п.). Запас B за последние 20 лет имел среднюю доходность 12 процентов, но более высокое стандартное отклонение — 30 п.п.Размышляя о риске, человек может решить, что Акция является более безопасным выбором. Даже если они не зарабатывают столько денег, они, вероятно, тоже не потеряют много денег. Человек может подумать, что среднее значение по Фонду B на 2 пункта не стоит дополнительного стандартного отклонения в 10 п.п. (больший риск или неопределенность ожидаемого дохода).
Правила для нормально распределенных номеров [изменить | изменить источник]
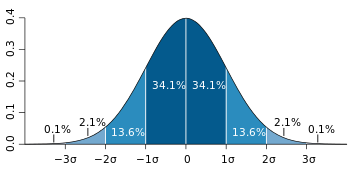 Темно-синий меньше стандартного отклонения от среднего. Для нормального распределения это включает 68.27 процентов чисел; в то время как два стандартных отклонения от среднего (средний и темно-синий) включают 95,45 процента; три стандартных отклонения (светлое, среднее и синее) включают 99,73 процента; и четыре стандартных отклонения составляют 99,994 процента.
Темно-синий меньше стандартного отклонения от среднего. Для нормального распределения это включает 68.27 процентов чисел; в то время как два стандартных отклонения от среднего (средний и темно-синий) включают 95,45 процента; три стандартных отклонения (светлое, среднее и синее) включают 99,73 процента; и четыре стандартных отклонения составляют 99,994 процента.Большинство математических уравнений для стандартного отклонения предполагают, что числа нормально распределены. Это означает, что числа распределены определенным образом по обе стороны от среднего значения. Нормальное распределение также называется гауссовым распределением , поскольку оно было открыто Карлом Фридрихом Гауссом. [4] Его часто называют кривой колокола , потому что числа растягиваются, чтобы сделать форму колокола на графике.
Числа обычно не распределяются, если они сгруппированы на одной стороне или другой стороне от среднего значения. Числа могут быть распределены и по-прежнему распределяются нормально. Стандартное отклонение говорит о том, насколько широко разбросаны числа.
Соотношение между средним (средним) и стандартным отклонением [изменить | изменить источник]
Среднее (среднее) и стандартное отклонение набора данных обычно записываются вместе.Тогда человек может понять, каково среднее число и насколько широко распространены другие числа в группе.
Распределение группы чисел также может быть задано коэффициентом вариации, который представляет собой стандартное отклонение, деленное на среднее значение. Это безразмерное число. Коэффициент вариации часто умножается на 100% и записывается в процентах.
Термин стандартное отклонение был впервые использован в письменной форме Карлом Пирсоном в 1894 году, [5] [6] после того, как он использовал его в лекциях.Это было в качестве замены более ранних имен для той же идеи: например, Гаусс использовал среднюю ошибку . [7]
- 01 Гаусс, Карл Фридрих (1816). «Bestimmung der Genauigkeit der Beobachtungen». Zeitschrift für Astronomie und verwandt Wissenschaften . 1 : 187–197.
- 01 Уокер, Хелен (1931). Исследования по истории статистического метода . Балтимор, MD: Williams & Wilkins Co. pp.24-25.
- ↑ «Что такое стандартное отклонение». Нетронутая. Получено 2011-10-29.
- — Кирквуд, Бетти Р; Стерн, Джонатан А.С. (2003). Основная медицинская статистика . Blackwell Science Ltd. CS1 maint: несколько имен: список авторов (ссылка)
- 01 Dodge, Yadolah (2003). Оксфордский словарь статистических терминов . Издательство Оксфордского университета. ISBN 0-19-920613-9 .
- 01 Пирсон, Карл (1894).«О разборе несимметричных частотных кривых». Фил. Сделка Рой. Soc. Лондон, серия А . 185 : 719–810.
- 01 Миллер, Джефф. «Самые ранние известные применения некоторых слов математики».

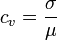
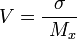 или
или