Page not found — Сайт ecoorg!
Unfortunately the page you’re looking doesn’t exist (anymore) or there was an error in the link you followed or typed. This way to the home page.
- ГЛАВНАЯ
- КОНТАКТ
- БЛОГ
- НОВОСТИ
- О СЕБЕ
- МЕТОДИЧЕСКАЯ РАБОТА.
- СОДЕРЖАНИЕ ЗАНЯТИЙ
- Основной капитал
- Оборотный капитал предприятия
- Трудовые ресурсы и оплата труда.
- Планирование деятельности организации.
- Основы экономики
- «Экономика и управление
- Презентации
- Управление персоналом
- ПМ 03 Планирование и организация работы персонала подразделения
- Экзаменационные вопросы
- Вопросы к дифференцированному зачету
- Темы докладов и рефератов.
- Презентации
- Оперативно-производственное планирование
- Методы контроля использования сырья и материалов в производстве
- Практические занятия
- ПЗ №3, №4 Расчет норм труда и производительности труда
- ПЗ №5, № 6 Расчет трудоемкости продукции и численности рабочих.

- ПЗ №7 , № 8 Расчет заработной платы рабочих при повременной и сдельной оплате труда.
- ПЗ №9, № 10, №11 Расчет годового фонда зарплаты рабочих и ИТР
- №45, №46 Анализ эффективности использования оборотных средств.
- П/З № 47, №48 Анализ расхода сырья и материалов в производстве продукции.
- ПЗ №49, №50 Анализ себестоимости продукции.
- ПЗ № 51, №52 Анализ показателей прибыли предприятия.
- ПЗ №53, № 54 Анализ показателей рентабельности предприятия
- Контрольная работа
- Курсовая работа
- Учебная практика
- Вопросы к диплому
- Презентация к экономическому расчету диплома
- ПМ 03 Участие в организации производственной деятельности структурного подразделения.
- Практические занятия
- ПЗ №1. «Расчет длительности производственного цикла
- ПЗ №4 Расчет графика ППР оборудования
- ПЗ №5 Расчет трудоемкости ремонтных работ
- ПЗ №6 Расчет численности ремонтных рабочих.

- ПЗ № 7 Расчет годового фонда заработной платы ремонтных рабочих.
- ПЗ № 8 Расчет затрат на вспомогательные материалы и запчасти для ремонтных работ
- ПЗ №9 Расчет себестоимости ремонтов оборудования.
- ПЗ № 16 Расчет графика сменности в производстве.
- ПЗ № 29 Выбор структуры управления
- ПЗ № 31, 32 Методы управления
- ПЗ № 34 Управленческие решения
- ПЗ № 36, № 38, № 39 Должностная инструкция мастера по ремонту оборудования
- ПЗ №40 Мотивация труда
- ПЗ № 41 Анализ мотивации персонала по методу В.И. Герчикова
- ПЗ №43 Оценка стиля руководства
- ПЗ № 45, 46 Составление плана проведения делового совещания, беседы
- ПЗ № 47, 48 Трансакции
- ПЗ № 49, № 50, № 51 Конфликты
- ПЗ № 55 , № 53, № 54 Графические методы управления
- ПЗ № 56 Расчет потребности персонала по методу трудоемкости и нормам обслуживания
- ПЗ № 58, №59 Оценка текучести кадров, подготовка документов по найму на работу
- ПЗ №60, №61 Анализ деловых ситуаций, формирование коллектива
- Задание на самостоятельную работу.

- Экзаменационные вопросы
- Дифференцированный зачет
- Учебная практика
- Дополнительные материалы для отчета по учебной практике.
- Курсовая работа
- Производственная практика
- диплом
- МОИ СТАТЬИ
- РАБОТЫ СТУДЕНТОВ
Blog
Рентабельность продукции: формула расчета и анализ
Рентабельность – одно из самых широко используемых экономических понятий. В нем отражена основная суть экономической деятельности – получение прибыли. Коэффициент рентабельности, собственно, и показывает нам, насколько эффективен тот или иной бизнес-процесс, насколько велика отдача от того или иного ресурса (материального, трудового или денежного). Иными словами, сколько прибыли на единицу измерения они приносят.Коэффициент рентабельности чего именно, спросите вы? Да чего угодно. Этот коэффициент высчитывается делением прибыли на любой из показателей деятельности предприятия. И умножением на 100%, соответственно.
И умножением на 100%, соответственно.
Делим чистую прибыль на размер собственного капитала (не забывая умножить на 100%) – получаем рентабельность собственного капитала. Делим чистую прибыль на размер активов – получаем рентабельность активов. На размер основных средств – рентабельность основных средств. На фонд оплаты труда и прочие затраты на сотрудников – рентабельность персонала. И так далее.
Можно посчитать рентабельность производства (делением валовой прибыли на объединенную стоимость основных фондов и оборотных средств). Рентабельность продаж (делением операционной прибыли на размер выручки).
Существует термин «порог рентабельности». Он означает минимальную прибыль, которая покрывает затраты по той или иной статье расходов. Очень важно найти этот порог, чтобы строить бизнес по правильным ориентирам и всегда понимать, за какую грань заходить нельзя.
Кстати, вы заметили, что при расчете разных видов рентабельности в расчет принимаются разные виды прибыли? Об отличиях между ними мы поговорим чуть позже.
А сейчас перейдем к основной теме.
Рентабельность реализуемой продукции – очень важный для производственной компании показатель. Он как бы «встроен» в рентабельность продаж. Разница в том, что прибыль в этом случае надо соотносить не с выручкой, а с себестоимостью продукции (этот показатель по умолчанию меньше выручки).
Рентабельность товарной продукции может быть рассчитана как в целом по ассортименту, так и по отдельным видам изделий.
Есть четыре основных формулы расчета рентабельности продукции. Варианты зависят от того, какая прибыль берется для расчета: чистая или прибыль от продаж. То же самое относится к себестоимости: она может быть либо полной, либо только производственной.
Подробнее о расчёте чистой прибыли
Вся необходимая информация есть в «Отчете о финансовых результатах» (форма 2 бухгалтерского баланса), который каждая компания обязана сдавать в налоговую инспекцию.
Соответственно, все приведенные ниже коды строк баланса относятся к форме 2. Условно обозначим рентабельность продукции как Rпр.
Условно обозначим рентабельность продукции как Rпр.
Итак, четыре формулы показателя рентабельности продукции.
1. По чистой прибыли и производственной себестоимости:
Rпр = (Строка 2400 / Строка 2120) Х 100%.
2. По чистой прибыли и полной себестоимости:
Rпр = (Строка 2400 / Сумма строк 2120, 2210 и 2220) Х 100%.
3. По прибыли от продаж и производственной себестоимости:
Rпр = (Строка 2200 / Строка 2120) Х 100%.
4. По прибыли от продаж и полной себестоимости:
Rпр = (Строка 2200 / Сумма строк 2120, 2210 и 2220) Х 100%.
Чтобы было нагляднее, приведем фрагмент «Отчета о финансовых результатах».
Наименование показателя | Код |
|---|---|
| Выручка | 2110 |
| Себестоимость продаж | 2120 |
| Валовая прибыль (убыток) | 2100 |
| Коммерческие расходы | 2210 |
| Управленческие расходы | 2220 |
| Прибыль (убыток) от продаж | 2200 |
| Доходы от участия в других организациях | 2310 |
| Проценты к получению | 2320 |
| Проценты к уплате | 2330 |
| Прочие доходы | 2340 |
| Прочие расходы | 2350 |
| Прибыль (убыток) до налогообложения | 2300 |
| Налог на прибыль | 2410 |
в т. ч. текущий налог на прибыль ч. текущий налог на прибыль | 2411 |
| отложенный налог на прибыль | 2412 |
| Прочее | 2460 |
| Чистая прибыль (убыток) | 2400 |
В бухгалтерской отчетности выделяют три основных уровня прибыли: валовую (балансовую), операционную (она же прибыль от продаж) и чистую.
Валовая прибыль (2100) – это выручка минус себестоимость (2110 минус 2120).
Прибыль от продаж (2200) – это валовая прибыль (2100) минус коммерческие (2210) и управленческие расходы (2220).
Коммерческие расходы включают в себя, к примеру, оплату транспорта, стоимость упаковки товара, заплату продавцов, затраты на рекламу и так далее. Управленческие расходы, в свою очередь – это зарплаты административного персонала (плюс представительские расходы), вложения в переподготовку кадров, оплата аудиторских и консалтерских услуг, и т.д.
Наконец, чистая прибыль (2400) образуется, когда из прибыли от продаж вычитают сумму налога на прибыль. Это упрощенная трактовка, более полная (но не окончательная формула выглядит как 2400 = 2200 + 2310 (доходы от участия в других организациях) + стр. 2320 (проценты к получению) – 2330 (проценты к уплате) + 2340 (прочие доходы) – 2350 (прочие расходы) – 2410 (налог на прибыль). Просто во многих случаях значения строк в середине формулы оказываются нулевыми, а значит, не оказывают влияния на результат.
Это упрощенная трактовка, более полная (но не окончательная формула выглядит как 2400 = 2200 + 2310 (доходы от участия в других организациях) + стр. 2320 (проценты к получению) – 2330 (проценты к уплате) + 2340 (прочие доходы) – 2350 (прочие расходы) – 2410 (налог на прибыль). Просто во многих случаях значения строк в середине формулы оказываются нулевыми, а значит, не оказывают влияния на результат.
С прибылью (первой частью формулы) разобрались. Теперь разберемся с себестоимостью продукции.
Чем различаются производственная себестоимость и полная себестоимость?
Производственная себестоимость, как мы уже выяснили, отражается в строке 2120 «Отчета о финансовых результатах».
Как правило, в нее включают следующие статьи затрат:
- стоимость сырья и материалов;
- стоимость потребляемой энергии;
- зарплата рабочих;
- отчисления с ФОТ рабочих;
- содержание и эксплуатация машин и оборудования;
- иные производственные расходы, в том числе на подготовку и освоение производства.

При расчете полной себестоимости к строке 2120 добавляются значения строк 2210 и 2220 (коммерческие и управленческие расходы).
Зачем нужно измерять рентабельность продукции?
К примеру, за 2019 год средний по экономике уровень рентабельности продукции составил 11,4%. А вот по отраслям разброс очень велик: от 66,3% в добыче металлических руд до 2,4% в производстве автотранспорта.
Но конечно же, дело не только в том, чтобы жить в ладу с налоговой инспекцией. Измерение рентабельности единицы продукции позволяет понять свою рыночную устойчивость, во-первых, по сравнению с конкурентами (на текущий момент), а во-вторых, проанализировать ее с развитием времени.
Конечно же, в идеале коэффициент рентабельности продукции с годами должен увеличиваться (до разумных пределов). Если ситуация обратная, это серьезный повод для беспокойства.
Как повысить рентабельность продукции
У нас есть числитель (прибыль) и есть знаменатель (себестоимость). Соответственно, надо наращивать первое (увеличивая наценку или улучшая маркетинговую стратегию), либо сокращать второе (более тщательно подходя к закупке материалов, оптимизируя затраты на персонал и т.д.).
Это не делается мановением пальца или по щучьему велению, рынок всегда накладывает свои ограничения. Но, по крайней мере, путь нам ясен.
это что, как рассчитать, где посмотреть?
Экономист, слыша слово деньги, представляет станки, ресурсы и даже людей. Действительно капитал может принимать разные формы: акций, средств производства, труда рабочей силы. В дополнение к этому, существует большое количество методов его учета. Что такое балансовая стоимость активов, где посмотреть ее в балансе и как она соотносится с балансовой стоимостью основных средств?
Что такое балансовая стоимость активов, где посмотреть ее в балансе и как она соотносится с балансовой стоимостью основных средств?
Что такое балансовая стоимость основных средств?
Балансовая стоимость основных средств – это показатель, который демонстрирует, сколько стоит все имущество фирмы согласно бухгалтерским данным (сюда также относятся сырье, полуфабрикаты, а также незавершенное производство, другими словами, все, что является активом фирмы).
Сведения о состоянии балансовой стоимости основных средств можно получить, взглянув на строку 1600 бухгалтерского баланса (ББ).
Все активы подразделяются на 2 вида: оборотные и внеоборотные.
- Оборотный капитал – это все имущество компании, полностью переносящее свою стоимость на произведенный товар за один свой оборот.
- Внеоборотные активы – это все имущество компании, приносящее прибыль, участвующее в производстве во время нескольких оборотов оборотных активов.
 Кстати, основные средства являются частью активов компании.
Кстати, основные средства являются частью активов компании.
Таким образом, балансовая стоимость основных средств фирмы эквивалентна сумме оборотных и внеоборотных средств.
Образец справки о балансовой стоимости активов предприятия.Балансовое стоимостное выражение основного капитала входит в состав балансовой стоимости активов предприятия.
Балансовая стоимость активов: как рассчитать и где посмотреть этот показатель в балансе?
Балансовая цена капитала фирмы вычисляется как сумма оборотного и внеоборотного капитала:
Сб=Со+Св;
Где:
- Сб – балансовое стоимостное выражение капитала фирмы
- Со – балансовое стоимостное выражение оборотных средств
- Св – балансовое стоимостное выражение внеоборотных активов
Как заработать в Инстаграм реальные деньги? Пошаговая инструкция содержится в публикации по ссылке.
Пример 1
Пусть фирма «Магнит» имеет оборотных активов, величину которых можно посмотреть в строке 1200 ББ, на сумму 300 000 р.. Величина внеоборотных активов (значение этого параметра можно посмотреть в строке 1100 ББ) составляет 700 000 р..
Балансовая стоимость активов имеет вид:
Сб=Со+Св=300 000 р. + 700 000 р. = 1 000 000 р.
где:
Сб – балансовое стоимостное выражение активов фирмы
Со – стоимость оборотных активов
Св – стоимость внеоборотных активов.
Образец справки о балансовой стоимости основных средств фирмы.Пример 2
Пусть предприятие «В» имеет оборотных активов на 200 000 р., а внеоборотных – на 500 000 р. Балансовая стоимостное выражение средств фирмы «В» будет равно сумме внеоборотных и оборотных активов:
200 000 р. + 500 000 р. = 700 000
Таким образом, балансовое стоимостное выражение средств предприятия «В» будет равно 700 000 р.
Порядок расчета балансовой стоимости основных средств
Основной капитал – собственность фирмы, которая приносит прибыль и участвует в более чем 1-ом производственном цикле в относительно неизменном виде (без учета износа).
Балансовая стоимость основных средств – это денежное выражение всех основных средств согласно бухгалтерскому учету. Почему здесь присутствует словосочетание «бухгалтерский учет»?
Для предприятия стоимость, к примеру, оборудования будет отличаться от простой покупки средства производства ввиду того, что для фирмы расходы на оборудование состоят из затрат на перевозку, монтаж и прочих издержек.
Сколько зарабатывают на ютубе за 1000 просмотров и как заработать на своем канале реальные деньги, вы можете узнать в нашей новой статье по ссылке.
Схема: Что такое балансовая стоимость?В бухучете объект может быть оценен разным образом. По этой причине важно, чтобы на балансе фирмы оборудование, к примеру, отображалось соответственно какому-нибудь методу бухучета.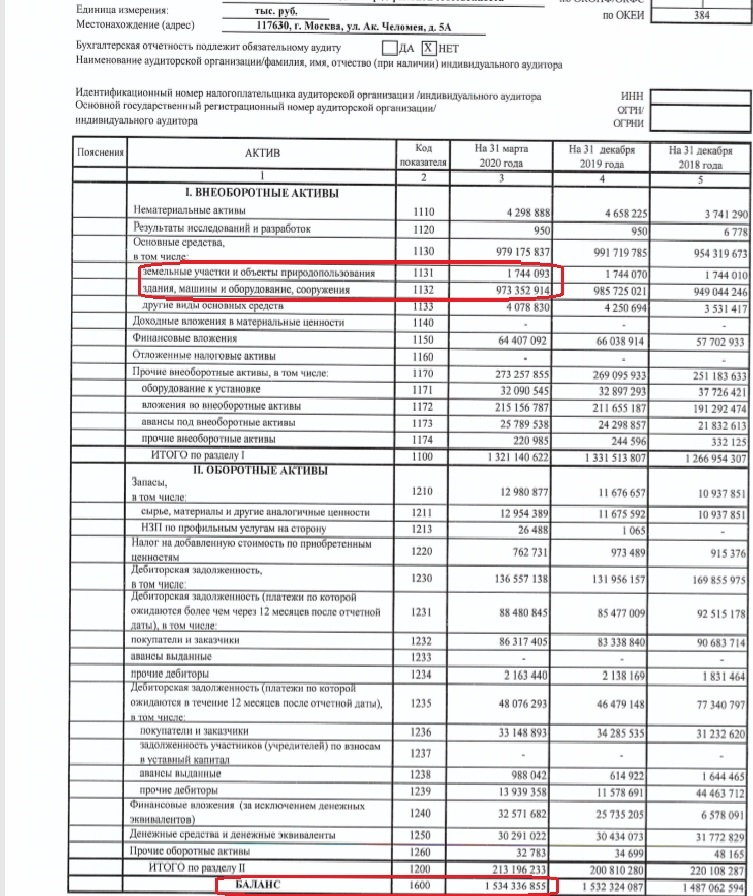 Связано это со спецификой предпринимательства.
Связано это со спецификой предпринимательства.
Для того, чтобы понять, как рассчитывается балансовая стоимость необходимо ввести несколько категорий.
Первоначальное стоимостное выражение основного капитала – это совокупность издержек, которые терпит предприниматель, содержит затраты на:
- Приобретение основного актива
- Его транспортировку
- Его монтаж
- Прочие цели, связанные с эксплуатацией средства производства.
Что такое рентабельность и как рассчитать рентабельность предприятия самостоятельно, вы можете прочесть по ссылке.
Со временем оборудование стареет морально (появляются новые технологии, и цена на него падает) или просто дорожает из-за специфики взаимодействия спроса и предложения. По этой причине производят переоценку стоимости основного капитала.
Основные понятия бухгалтерского учета.Есть ряд типов учетной политики (методологий учета активов предприятия). При учетной политике, основанной на первоначальной цене объекта учета, предполагается, что на всем протяжении бухучета актив будет учитываться как разность от первоначальной стоимости и величины износа основного средства (амортизацией).
При учетной политике, основанной на первоначальной цене объекта учета, предполагается, что на всем протяжении бухучета актив будет учитываться как разность от первоначальной стоимости и величины износа основного средства (амортизацией).
Учетная политика, в основном принципе которой находится переоценка, подразумевает, что предприниматель будет проводить регулярную переоценку своих основных фондов, пользуясь помощью экспертов.
Следующая категория, которую нужно ввести для полного понимания того, что из себя представляет балансовое стоимостное выражение основного капитала, тесно переплетена с видом учетной оценки, основанной на регулярной переоценке основного капитала.
Какая предусмотрена ответственность главного бухгалтера с 2016 года и какие изменения произошли в законодательстве в этом году, вы можете прочесть тут.
Восстановительное стоимостное выражение основного капитала показывает, во сколько предприятию обойдется создание объекта основных фондов при текущих ценах на рабочую силу, комплектующие, материалы и другие ресурсы, необходимые для доведения его до рабочего состояния, а также учитывает изменение стоимости средства производства из-за его морального износа (ввиду появления новых технологий). Рассчитывается на основании экспертных оценок.
Рассчитывается на основании экспертных оценок.
Балансовая стоимость основных средств может рассчитываться по первоначальной стоимости и восстановительной. Выбор метода зависит от того, когда проводилась переоценка основных фондов.
Схема расчета среднегодовой балансовой стоимости основных средств.Если переоценка проводилась после введения в эксплуатацию основного актива, то он учитывается по восстановительной стоимости, если до – по первоначальной. Что делать, если основное средство уже использовалось, а на балансе предприятия оно окажется впервые?
При таком положении дел обычно используются три разных метода: рыночный (экспертное определение стоимости средства производства на базе текущих рыночных цен), доходный (основывается на расчёте будущего совокупного потока денежных средств от актива, который и является стоимостью основного фонда), метод расчёта восстановительной стоимости.
Балансовое стоимостное выражение основного капитала равно сумме всех первоначальных и восстановительных стоимостей основных средств предприятия.
Иногда восстановительная стоимость рассчитывается на основе не первоначальной стоимости (вычисляется показатель, демонстрирующий, как изменилась цена средства производства, а затем он умножается на первоначальную стоимость актива), а по остаточной стоимости. При выборе опираются на специфику конкретной фирмы и действующие нормы налогообложения.
Остаточная стоимость – это величина, которая вычисляется следующим образом: из первоначального, или восстановительного стоимостного выражения средства производства (в соответствии с тем, до, или после переоценки объект вводился в эксплуатацию) вычитается сумма износа за фактический эксплуатационный период. Таким образом, остаточная стоимость показывает реальную текущую стоимость основных фондов.
Образец бизнес-плана с расчетами и пошаговая инструкция по его составлению содержатся в этой статье.
Пример 1
Пусть предприятие «Преимущество» имеет станок А, купленный за 100 000 р. (включая пошлину за прибыль). Затраты на транспортировку составили 8 000 р., на установку – 6 000 р., прочие издержки – 3 000 р. Была произведена переоценка основных фондов.
(включая пошлину за прибыль). Затраты на транспортировку составили 8 000 р., на установку – 6 000 р., прочие издержки – 3 000 р. Была произведена переоценка основных фондов.
После этого предприятие купило станок Б, расходы на покупку которого составили 60 000 р. (включая пошлину за прибыль), на транспортировку – 7 000 р., на установку – 5 000 р., а прочие расходы составили 1 500 р.
С момента покупки станка А его стоимость упала на 20%. Абстрагировавшись от частностей, рассчитаем балансовую стоимость основных средств для данной ситуации. Станок А был введен в эксплуатацию до переоценки, поэтому на балансе его надо учитывать по восстановительной стоимости.
Восстановительная стоимость равна результату от произведения первоначального стоимостного выражения актива на показатель морального износа, которое эквивалентно изменению стоимости средства производства, выраженное в процентах.
Св =(Зп+Зпер+Зм+Ид)*Кми;
где:
- Св – восстановительная стоимость
- Зп – затраты на покупку
- Зпер – затраты на перевозку средства производства
- Зм – расходы на монтаж
- Ид – другие издержки;
- Кми – коэффициент морального износа (коэффициентом морального износа в данном случае является снижение стоимости станка, как стоимостное выражение морального износа)
По формуле получаем:
(100 000 р. + 8 000 р. + 6 000 р. + 3 000 р.) *0.8 = 93 600 р. (т. к. стоимость упала на 20%, текущая цена равна: 1 минус 0.2 – 0.8 от первоначальной стоимости).
+ 8 000 р. + 6 000 р. + 3 000 р.) *0.8 = 93 600 р. (т. к. стоимость упала на 20%, текущая цена равна: 1 минус 0.2 – 0.8 от первоначальной стоимости).
Станок Б был введен в эксплуатацию после переоценки, поэтому его балансовая стоимость рассчитывается как первоначальная, которая по формуле:
Сперв=Зп+Зт+Зу+Зпр;
где:
- Сперв – первоначальная стоимость
- Зп – затраты на покупку станка
- Зт – затраты на транспортировку станка
- Зу – затраты на установку станка
- Зпр – прочие затраты;
равна: 60 000 р. + 7 000 р. + 5 000 р. + 1 500 р. = 73 500 р.
Балансовое стоимостное выражение основного капитала в данной ситуации равна сумме балансовых стоимостей станка А и станка Б:
93 600 р. + 73 500 р. = 167 100
Образец расчета балансовой стоимости основных средств в программе ОС.Таким образом, балансовая стоимость основных средства предприятия «Преимущество» равна 167 100 р.
Пример 2
Пусть предприятие «Г» имеет станок А, купленный за 250 000 р. (включая пошлину за прибыль). Издержки по транспортировке станка составили 7 000 р., по установке – 5 000 р., другие издержки составили 2 500. С момента приобретения станка его стоимость выросла на 15%. Была произведена переоценка основных средств.
После этого был куплен станок Б по стоимости – 150 000 р. (включая пошлину за прибыль). Затраты на транспортировку составили 4 500 р., на установку – 3 500 р., прочие затраты составили 2 000 р.. Рассчитаем балансовую стоимость основного капитала, опираясь на исходные данные.
Станок А был введен в эксплуатацию до переоценки, поэтому его стоимость рассчитывается как восстановительная, которая по формуле:
Св=(Зп+Зт+Зу+Зпр)*Кми
где:
- Св – восстановительная стоимость
- Зп – затраты на покупку станка
- Зт – затраты на транспортировку станка
- Зу – затраты на установку станка
- Зпр – прочие затраты
- Кми – коэффициент морального износа станка;
равна:
(250 000 р. + 7 000 р. + 5 000 р. + 2 500 р.) * 1,15= 304 175 р. (В данном случае рост цен превысил величину морального износа, поэтому коэффициент морального износа, согласно правилам пропорции, составил: 1 + 0.15 = 1.15).
+ 7 000 р. + 5 000 р. + 2 500 р.) * 1,15= 304 175 р. (В данном случае рост цен превысил величину морального износа, поэтому коэффициент морального износа, согласно правилам пропорции, составил: 1 + 0.15 = 1.15).
Станок Б был куплен после проведения переоценки, поэтому его балансовая стоимость рассчитывается как первоначальная, которая по формуле:
Сперв=Зп+Зпер+Зм+Ид;
где:
- Сперв – первоначальная стоимость
- Зп – затраты на покупку
- Зпер – затраты на перевозку
- Зм – затраты на монтаж
- Ид – другие издержки;
равна:
150 000 р. + 4 500 р. + 3 500 р. + 2 000 р. = 160 000 р.
Балансовая стоимость основных средств, которая в данной ситуации эквивалентна сумме восстановительной стоимости станка А и первоначальной стоимости станка Б, составляет: 304 175 р. + 160 000 р. = 464 175 р.
Какая предусмотрена ответственность за неуплату налогов юридическим лицом – узнайте здесь.
Итак, балансовое стоимостное выражение основного капитала входит в состав балансовой стоимости активов предприятия. Для расчёта стоимостного выражения основного средства применяются разные методы.
Что такое балансовый отчет? Анализ балансового отчета на примере компании Apple вы можете посмотреть в следующем видео:
Не забудьте добавить «FBM.ru» в источники новостей
Где в балансе отражается незавершенное строительство, в какой строке
По данной строке Бухгалтерского баланса отражается информация об объектах основных средств (ОС), учитываемых в бухгалтерском учете на счете 01 «Основные средства». По вопросу отражения в Бухгалтерском балансе незавершенных капитальных вложений, учитываемых на счете 08 «Вложения во внеоборотные активы» (кроме субсчетов 08-5 и 08-8), в настоящее время существует две позиции.
По вопросу отражения в Бухгалтерском балансе незавершенных капитальных вложений, учитываемых на счете 08 «Вложения во внеоборотные активы» (кроме субсчетов 08-5 и 08-8), в настоящее время существует две позиции.
Первая позиция заключается в том, что величина незавершенных капитальных вложений в объекты, которые впоследствии будут приняты к учету на счете 01, включается в показатель строки 1150 и отражается обособленно по одной из строк, расшифровывающих показатель этой строки. Данная позиция основана на том, что в форме Бухгалтерского баланса, утвержденной Приказом Минфина России от 02.07.2010 N 66н, отсутствует отдельная строка «Незавершенное строительство». При этом согласно п.
20 ПБУ 4/99 статья «Незавершенное строительство» включается в группу статей «Основные средства», а п. 3 Приказа Минфина России от 02.07.2010 N 66н позволяет организациям самостоятельно определять детализацию показателей по статьям отчетов. Кроме того, в Приложении N 3 к Приказу Минфина России от 02. 07.2010 N 66н приводится Пример оформления Пояснений к Бухгалтерскому балансу и Отчету о финансовых результатах. В данном Примере разд.
07.2010 N 66н приводится Пример оформления Пояснений к Бухгалтерскому балансу и Отчету о финансовых результатах. В данном Примере разд.
Незавершенное производство в балансе: строка
2 «Основные средства» включает таблицу 2.2 «Незавершенные капитальные вложения».
Вторая позиция состоит в том, что информация о незавершенных капитальных вложениях не отражается по строке 1150 «Основные средства». Такой вывод следует из норм ПБУ 6/01 (более позднего, чем упомянутое выше ПБУ 4/99). В частности, требования к раскрытию информации об основных средствах в бухгалтерской отчетности установлены п. 32 ПБУ 6/01, в котором отсутствует какое-либо упоминание незавершенных капитальных вложений или незавершенного строительства. Кроме того, само ПБУ 6/01 «Основные средства» не применяется в отношении капитальных вложений, так как они не удовлетворяют условиям принятия к учету в составе основных средств (п. п. 3, 4 ПБУ 6/01). Дополнительным аргументом в пользу данной позиции является то, что в Положении по ведению бухгалтерского учета и бухгалтерской отчетности в Российской Федерации в разделе «Правила оценки статей бухгалтерской отчетности» подраздел «Незавершенные капитальные вложения» присутствует наравне с подразделом «Основные средства».
Таким образом, организациям предстоит самостоятельно с учетом приведенных выше аргументов принять решение, включать величину незавершенных капитальных вложений в показатель строки 1150 «Основные средства» или не включать. В последнем случае величина незавершенных капитальных вложений может быть отражена в разд. I «Внеоборотные активы» по отдельной самостоятельно введенной организацией строке «Незавершенные капитальные вложения», а в случае несущественности показателя — по строке 1190 «Прочие внеоборотные активы» (по вопросу раскрытия данных о незавершенных капитальных вложениях см. также Письмо Минфина России от 27.01.2012 N 07-02-18/01).
Отметим, что при решении вопроса об отражении в Бухгалтерском балансе незавершенных капитальных вложений целесообразно применить единый подход к отражению всех видов вложений во внеоборотные активы.
ДОПОЛНИТЕЛЬНО по данному вопросу см. Письмо Минфина России от 06.12.2011 N 03-05-05-01/95.
2.22: В какой строке MySQL находится максимальное значение по группе?
Главная Страница » Книги по PHP » MySQL уроки для начинающих с нуля » В какой строке находится максимальное значение по группе
Для каждого изделия найдите торгового агента с наиболее высокой ценой.
В MySQL проще всего добиться такого эффекта так:
- Получите список из записей (изделие, максимальная цена).
- Для каждого изделия получите из таблицы соответствующие строки, которые имеют максимальную цену.
Это может быть легко выполнено через временную таблицу, которая нужна только для хранения промежуточного набора данных. Это довольно сложная последовательность действий, поэтому рассмотрим ее по шагам. Сначала создайте в базе данных временную таблицу:
Как видите, во временной таблице всего два столбца: один для кода изделия изделия (article), другой для цены (price). Ключевое слово TEMPORARY означает временно созданную таблицу для хранения промежуточных данных.
Теперь надо проследить вот за каким сложным моментом. Дело в том, что MySQL представляет собой многопользовательскую систему. Это значит, что пока вы работаете с таблицей, с ней может работать кто-то еще (таких «кого-то еще» может быть сколько угодно). Друг о друге вы не знаете ничего, равно как и о том, кто и что с таблицей делает. Знать это вам незачем.
Знать это вам незачем.
Но вот проблема: что будет, если в тот момент, когда вы получаете из таблицы данные для своего анализа, кто-то возьмет и поменяет их? Ни к чему страшному это не приведет, но вы получите устаревшие данные, изменений вы не увидите. Значит, надо помешать внести изменения до тех пор, пока вы не закончите расчеты. Это делается с помощью блокировки.
строки 1150 и 1190 баланса
Тема блокировок обширна и сложна, а потому рассматривается в последующих главах.
Но сейчас рассмотрим наиболее простой вариант. Итак, надо блокировать таблицу shop. Нам не требуется сделать таблицу совсем недоступной. Нужно только, чтобы никто не мог вносить в нее изменения. А вот читать таблицу другие пользователи смогут. Приступим:
Если вы не используете таблицу TEMPORARY, вы должны также блокировать и таблицу tmp.
Слово read в этой команде означает, что вы разрешили другим пользователям сервера читать таблицу. А вот тут понятие потока может привести к недопониманию.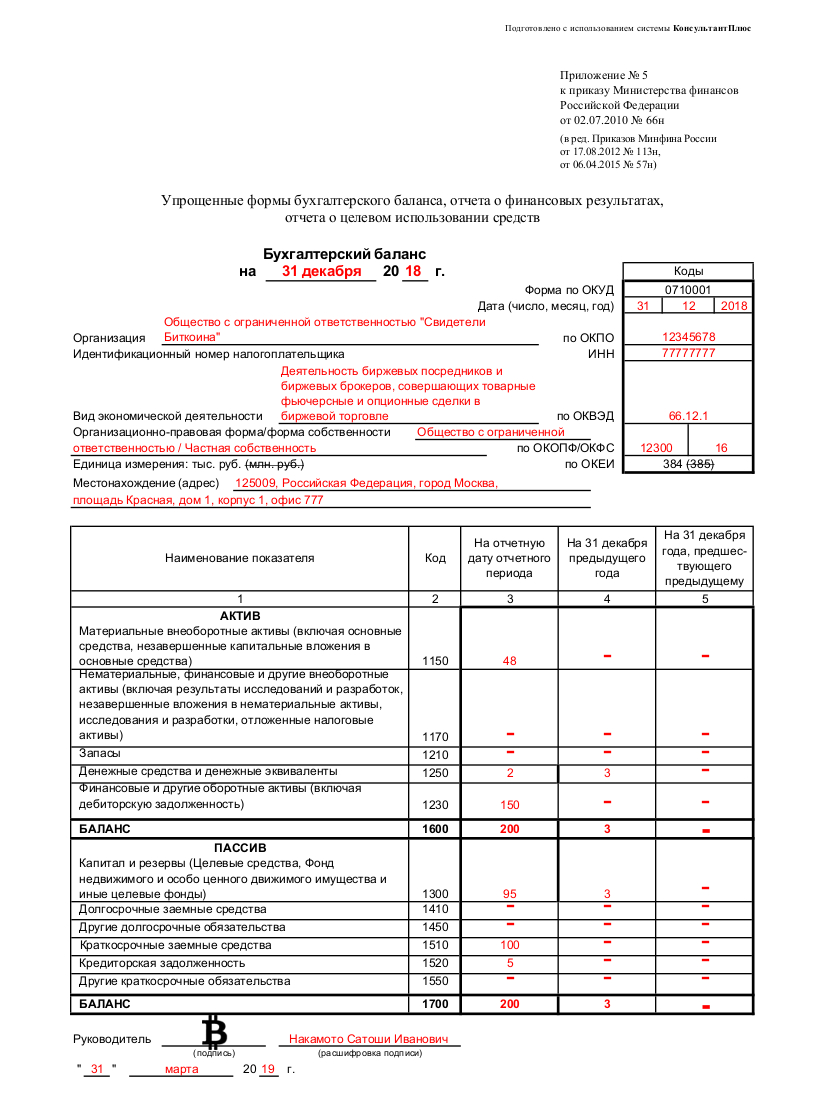 Дело в том, что блокировка таблицы распространяется на все потоки, за исключением того, который эту блокировку создал.
Дело в том, что блокировка таблицы распространяется на все потоки, за исключением того, который эту блокировку создал.
Казалось бы: ну и что? А вот что: если вы открыли несколько копий клиента и установили не одно соединение с сервером, то блокировка таблицы распространится и на все ваши соединения, исключая то, в котором вы блокировку поставили. Соответственно, и снять блокировку вы сможете только в том же самом соединении.
Неважно, что вы регистрировались на сервере под одним и тем же логином во всех соединениях. Важно то, что блокировка привязана к конкретному соединению, а не к пользователю. Такая ситуация часто приводит начинающих пользователей к ошибке: они ставят блокировку на одном соединении, а снять пытаются из другого. Не выйдет, сервер не позволит.
Теперь начинается то, ради чего мы блокировали таблицу. Выберем из нее нужные данные и наполним ими подготовленную временную таблицу:
Как видите, здесь применен еще один хитрый прием. Вместо того, чтобы перечислять в операторе INSERT вводимые значения (используя слово VALUES), мы подставили оператор SELECT непосредственно вместо них. Что при этом произойдет? А вот что: оператор SELECT найдет и вернет строки, но вместо отображения на экране они попадут прямо в оператор INSERT, который вставит их в таблицу tmp. Таким образом, один запрос может быть вложен в другой (здесь SELECT вложили в INSERT). Возьмите на заметку для последующего использования.
Что при этом произойдет? А вот что: оператор SELECT найдет и вернет строки, но вместо отображения на экране они попадут прямо в оператор INSERT, который вставит их в таблицу tmp. Таким образом, один запрос может быть вложен в другой (здесь SELECT вложили в INSERT). Возьмите на заметку для последующего использования.
Вот теперь найдем максимальную цену. В запросе используются две таблицы (shop и tmp), а раз так, то применяются имена столбцов с указанием таблицы, из которой надо извлечь данные:
Отлично, данные получены. Теперь дадим возможность другим пользователям работать с блокированной таблицей в полном объеме (а не только читать ее):
Эта команда сняла любые блокировки, установленные текущим потоком, со всех заблокированных вами таблиц. Подробнее о блокировках мы еще будем говорить позже (и немало: тема сложная), а пока удалим ставшую лишней временную таблицу со всеми данными в ней:
Команда DROP предназначена для удаления чего-либо. Поскольку сейчас надо удалить таблицу, указано ключевое слово TABLE (таблица), а затем ее имя. Вообще учите английский язык! SQL отличается от языков программирования как раз тем, что работаете вы с ним пусть и на очень упрощенном, но вполне понятном английском языке. Большинство слов совпадает. Подробнее о команде DROP будет рассказано позже, в главе 7, где рассмотрены действия с таблицами.
Вообще учите английский язык! SQL отличается от языков программирования как раз тем, что работаете вы с ним пусть и на очень упрощенном, но вполне понятном английском языке. Большинство слов совпадает. Подробнее о команде DROP будет рассказано позже, в главе 7, где рассмотрены действия с таблицами.
Можно ли было все это сделать одиночным запросом?
Да, но только используя совершенно не эффективный прием МАХ-СОNкошка, который приводится только в справочных целях:
Поделиться с друзьями
Строка 130 «Незавершенное строительство«Главная/ Бухгалтерская отчетность/ Строка 130
Строка 130 бухгалтерской отчетности относится к бухгалтерскому балансу до 2011 года.
130 Незавершенное строительство
Прежде всего следует отметить, что наименование этой строки нужно понимать в широком смысле.
Незавершенное строительство и средства дольщиков: как выгоднее показать в балансе
Под «незавершенным строительством» понимается сумма незавершенных капитальных вложений. Это расходы на незаконченные строительно-монтажные работы и прочие капитальные работы и затраты (проектно-изыскательские, геолого-разведочные и буровые работы, затраты по отводу земельных участков и
Это расходы на незаконченные строительно-монтажные работы и прочие капитальные работы и затраты (проектно-изыскательские, геолого-разведочные и буровые работы, затраты по отводу земельных участков и
переселению, связанные со строительством, затраты на формирование основного стада продуктивного и рабочего скота и т. д.). Кроме того, по строке 130 отражаются затраты на приобретение нематериальных активов и основных средств, требующих и не требующих монтажа, до их ввода в эксплуатацию. По строке 130 указывается сумма затрат на работы, выполняемые как хозяйственным, так и подрядным способом. Незавершенные капитальные вложения отражаются в балансе по фактическим затратам для застройщика (инвестора).
Если согласно учетной политике организация не переводит на счет 01 «Основные средства» построенные или приобретенные объекты недвижимости до получения документов, подтверждающих государственную регистрацию права собственности, а продолжает учитывать их на отдельном субсчете счета 08 «Вложения во внеоборотные активы», то стоимость этих объектов недвижимости тоже следует отражать по строке 130.
Обратите внимание: по объектам недвижимости, по которым закончено капитальное строительство, оформлен акт приемки-передачи, документы переданы на государственную регистрацию права собственности и которые фактически эксплуатируются организацией, следует начислять амортизацию в общеустановленном порядке. Причем независимо от того, на каком счете — 01 «Основные средства» или 08 «Вложения во внеоборотные активы» — ведется учет этих объектов недвижимости. Это требование установлено пунктом 52 Методических указаний по учету основных средств. Следовательно, при составлении баланса стоимость таких объектов недвижимости, учитываемых на счете 08, следует отражать за минусом сумм амортизации, начисленной по этим объектам на счете 02.
Показатель строки 130 формируется как сумма остатков по дебету счетов:
- 07 «Оборудование к установке»;
- 08 «Вложения во внеоборотные активы»;
- 16 «Отклонения в стоимости материальных ценностей» (в части отклонений, относящихся к имуществу, стоимость которого отражена на счетах 07 и 08).

Обратите внимание: по строке 130 баланса в составе затрат по незавершенному строительству нельзя отражать суммы авансов, перечисленные поставщикам и подрядчикам. Согласно пункту 3 ПБУ 10/99 «Расходы организации» суммы авансов и предоплаты не признаются расходами организации. По строке 130 баланса отражаются фактические затраты организации на капитальные вложения, а суммы авансов к таковым не относятся. Они формируют дебиторскую задолженность, которая отражается по соответствующим строкам актива баланса (см. комментарий к строке 240 баланса на с. 410).
Напомним: существенные показатели деятельности организация вправе показать отдельно. Если капитальные вложения организации носят разноплановый характер, то для расшифровки показателя строки 130 она может ввести в форму баланса дополнительные строки.
Полезные ссылки
►Экономическая литература◄ ►Методика финансового анализа◄ ►Формы бухгалтерской отчетности◄ ►Крупнейшие АО России◄
Строка 213 «Затраты в незавершенном производстве«Главная/ Бухгалтерская отчетность/ Строка 213
Строка 213 бухгалтерской отчетности относится к бухгалтерскому балансу до 2011 года.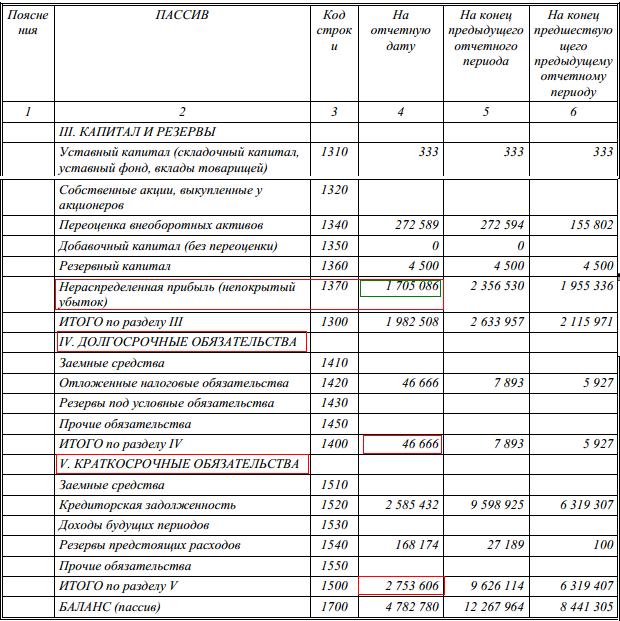
Строка 213 «Затраты в незавершенном производстве»
К затратам незавершенного производства относятся продукция (работы), не прошедшая всех стадий (фаз, переделов), предусмотренных технологическим процессом, а также изделия неукомплектованные, не прошедшие испытания и технической приемки.
По строке 213 показывается сумма дебетовых остатков по счетам:
- 20 «Основное производство»;
- 21 «Полуфабрикаты собственного производства»;
- 23 «Вспомогательные производства»;
- 29 «Обслуживающие производства и хозяйства»;
- 44 «Расходы на продажу»;
- 46 «Выполненные этапы по незавершенным работам».
В бухгалтерском учете незавершенное производство (НЗП) в массовом и серийном производстве может отражаться:
- по фактической или нормативной (плановой) производственной себестоимости;
- по прямым статьям затрат;
- по стоимости сырья, материалов и полуфабрикатов.
При единичном производстве продукции незавершенное производство отражается по фактически произведенным затратам.
Организация самостоятельно выбирает методы оценки незавершенного производства и закрепляет выбор в приказе по учетной политике.
В балансе НЗП отражается в той же оценке, что и в бухгалтерском учете. Сумма НЗП должна быть подтверждена соответствующими расчетами (бухгалтерскими справками).
Если неторговая организация распределяет коммерческие расходы между реализованной и нереализованной продукцией (товарами, услугами), то при заполнении строки 213 берется не весь остаток по счету 44 «Расходы на продажу».
Строка 1150 «Основные средства»
Несписанные расходы на упаковку и транспортировку, учтенные в составе коммерческих расходов на счете 44, отражаются по строке 217 «Прочие запасы и затраты» баланса, а не по строке 213.
Строительные, научные, проектные, геологические и т. п. организации, которые осуществляют расчеты с заказчиками в соответствии с заключенными договорами поэтапно, по строке 213 отражают стоимость частично принятых заказчиком работ (дебетовое сальдо счета 46 «Выполненные этапы по незавершенным работам»). Напомним, что стоимость законченных этапов работ, отраженная в подписанных заказчиком формах № КС-2 и КС-3, учитывается по дебету счета 46 в корреспонденции со счетом 90 «Продажи».
Напомним, что стоимость законченных этапов работ, отраженная в подписанных заказчиком формах № КС-2 и КС-3, учитывается по дебету счета 46 в корреспонденции со счетом 90 «Продажи».
Полезные ссылки
►Экономическая литература◄ ►Методика финансового анализа◄ ►Формы бухгалтерской отчетности◄ ►Крупнейшие АО России◄
Пассив и актив баланса
Бухгалтерский баланс — основная форма бухгалтерской отчетности. Он характеризует имущественное и финансовое состояние организации на отчетную дату. В балансе отражаются остатки по всем счетам бухгалтерского учета на отчетную дату. Эти показатели приводятся в бухгалтерском балансе в определенной группировке. Бухгалтерский баланс делится на две части: актив и пассив. Сумма активов баланса всегда равна сумме пассивов баланса.
Актив балансаЛюбая собственность предприятия — машины и оборудование, недвижимость, финансовые вложения, задолженность дебиторов и т. д.
д.
Недострой на балансе
— является его активами. Это все то, что можно обратить в денежные средства.
Активы подразделяются на:
- Нематериальные активы
- Основные средства
- Незавершенное строительство
- Доходные вложения в материальные ценности
- Долгосрочные финансовые вложения
- Отложенные налоговые активы
- Прочие внеоборотные активы
- Запасы
- Налог на добавленную стоимость по приобретенным ценностям
- Дебиторская задолженность (платежи по которой ожидаются более чем через 12 месяцев после отчетной даты)
- Дебиторская задолженность (платежи по которой ожидаются в течение 12 месяцев после отчетной даты)
- Краткосрочные финансовые вложения
- Денежные средства
- Прочие оборотные активы
Пассивы организации — это источники формирования ее активов. К ним относятся капиталы, резервы, а также кредиторские обязательства, возникшие у организации в процессе ведения хозяйственной деятельности.
Пассивы подразделяются на:
- Капитал и резервы
- Уставный капитал
- Собственные акции, выкупленные у акционеров
- Добавочный капитал
- Резервный капитал
- Нераспределенная прибыль (непокрытый убыток)
- Займы и кредиты
- Отложенные налоговые обязательства
- Прочие долгосрочные обязательства
- Займы и кредиты
- Кредиторская задолженность
- Задолженность перед участниками (учредителями) по выплате доходов
- Доходы будущих периодов
- Резервы предстоящих расходов
- Прочие краткосрочные обязательства
Нематериальные активы — неденежный актив, не имеющий физической формы.
Основны́е сре́дства (ОС) (или Основные производственные фонды (ОПФ)) — отражённые в бухгалтерском или налоговом учёте основные фонды организации в денежном выражении.
«Незавершенное строительство» — это сумма незавершенных капитальных вложений.
Доходные вложения в материальные ценности — вложения организации в часть имущества, здания, помещения, оборудование и другие ценности, имеющие материально-вещественную форму, предоставляемые организацией за плату во временное пользование (временное владение и пользование) с целью получения дохода
Долгосрочные финансовые вложения — вложение свободных денежных средств предприятия, срок погашения которых превышает один год:
— средства, направленные в уставные капиталы других предприятий;
— средства, направленные на приобретение ценных бумаг других предприятий;
— долгосрочные займы, выданные другим предприятиям; и т.п.
Отложенные налоговые активы представляют собой часть отложенного налога на прибыль, задача которой привести к уменьшению размера налога, который необходимо уплатить в бюджет в отчетный период.
Внеоборотные активы — активы с продолжительностью использования более одного года: долгосрочные финансовые вложения, нематериальные активы, основные средства, прочие долгосрочные активы.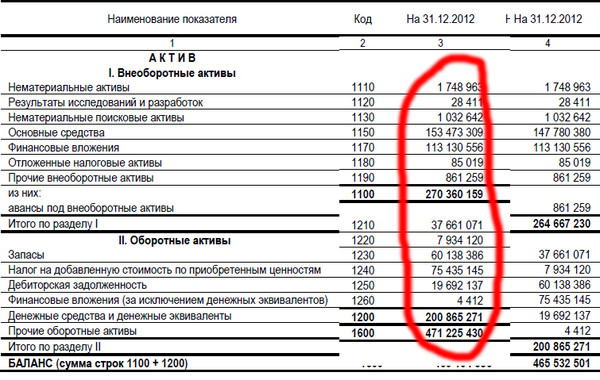
Материально-производственные запасы — активы, используемые в качестве сырья, материалов и т. п. при производстве продукции, предназначенной для продажи (выполнения работ, оказания услуг), приобретаемые непосредственно для перепродажи, а также используемые для управленческих нужд организации.
Налог на добавленную стоимость по приобретенным ценностям
— счет, предназначенный для обобщения информации об уплаченных (причитающихся к уплате) предприятием суммах налога на добавленную стоимость по приобретенным ценностям.
Краткосрочные финансовые вложения — краткосрочные (на срок не более одного года) финансовые вложения предприятия в доходные активы (акции, облигации и другие ценные бумаги) других предприятий, объединений и организаций, денежные средства на срочных депозитных счетах банков, процентные облигации государственных и местных займов и др. — являются наиболее легко реализуемыми активами.
Пассив балансаУста́вный капитал — это сумма средств, первоначально инвестированных собственниками для обеспечения уставной деятельности организации; уставный капитал определяет минимальный размер имущества юридического лица, гарантирующего интересы его кредиторов
Доба́вочный капита́л — статья пассива баланса, складывающаяся из следующих элементов:
- эмиссионный доход — разница между продажной и номинальной стоимостью акций предприятия;
- курсовые разницы — разницы при оплате доли уставного капитала в иностранной валюте;
- разница при переоценке основных средств — разница при изменении стоимости основных средств.

Резе́рвный капита́л — размер имущества предприятия, который предназначен для размещения в нём нераспределённых прибылей, для покрытия убытков, погашения облигаций и выкупа акций предприятия, а также для других целей.
- Краткосрочные обязательства
Кредиторская задолженность — задолженность субъекта (предприятия, организации, физического лица) перед другими лицами, которую этот субъект обязан погасить.
Резервы предстоящих расходов
В целях равномерного включения предстоящих расходов в издержки производства или обращения организация может создавать резервы на: предстоящую оплату отпусков работникам; выплату ежегодного вознаграждения за выслугу лет; выплату вознаграждений по итогам работы за год; ремонт основных средств; производственные затраты по подготовительным работам в связи с сезонным характером производства; предстоящие затраты на рекультивацию земель и осуществление иных природоохранных мероприятий; предстоящие затраты по ремонту предметов, предназначенных для сдачи в аренду по договору проката; гарантийный ремонт и гарантийное обслуживание; покрытие иных предвиденных затрат и другие цели, предусмотренные законодательством Российской Федерации, нормативными актами Министерства финансов Российской Федерации.
Оптимальный поток мощности — документация PyPSA 0.17.1
См. Модуль pypsa.opf и pypsa.linopf . Оптимизация с помощью линеаризованных уравнений потока мощности для (смешанного) переменного тока
и сети постоянного тока полностью поддерживаются. Обратите внимание, что оптимизация с использованием полных нелинейных уравнений потока мощности еще не поддерживается.
Все ограничения и переменные перечислены ниже.
Обзор
Линейный модуль OPF может оптимизировать диспетчеризацию генерации и хранения, а также мощности инфраструктуры генерации, хранения и передачи.
Предполагается, что нагрузка неэластична и должна выдерживаться в каждом снимке (в будущих версиях это будет ослаблено).
В настоящее время оптимизация использует непрерывные переменные для большинства функций; Для генераторов также реализовано обязательство единицы с бинарными переменными.
Целевая функция — это общая стоимость системы для оптимизированных снимков.

Каждому снимку может быть присвоен вес \ (w_t \) для представления e.грамм. несколько часов.
Эту настройку также можно использовать для стохастической оптимизации, если вы интерпретируете взвешивание как вероятность.
Каждый объект передачи имеет капитальные затраты.
У каждого актива для генерации и хранения есть капитальные и предельные затраты.
Выполнить:
network.lopf (снимки, solver_name = "glpk", solver_io = None,
extra_functionality = Нет, solver_options = {},
keep_files = Ложь, формулировка = "углы",
extra_postprocessing = Нет) ``
, где снимков — итерация снимков, solver_name — это
строка, e.грамм. «Gurobi» или «glpk», solver_io — строка, extra_functionality — это функция сети и снимков, которая
вызывается перед решателем (см. ниже), extra_postprocessing — это
функция сети, снимков и двойников, которая вызывается после решения
(см. ниже),
ниже), solver_options — это словарь флагов для передачи
решатель, keep_files означает, что файл .lp сохранен и формулировка — строка в ["углы", "циклы", "Кирхгоф", "ptdf"] (см. Формулировки пассивного ветвления потока
Больше подробностей).
- Network.lopf ( снимков = Нет , pyomo = True , solver_name = ‘glpk’ , solver_options = {} , solver_logfile = Нет , формулировка = ‘kirchhoff’ , keep_files = False , extra_functionality = Нет , ** kwargs )
Линейный оптимальный поток мощности для группы снимков.
- Параметры
снимков ( список или индексный фрагмент ) — список снимков для оптимизации, должен быть подмножеством сеть.снимки, по умолчанию network.snapshots
pyomo ( bool , по умолчанию True ) — Использовать ли pyomo для построения и решения модели, настройка это значение False экономит много памяти и времени.

solver_name ( string ) — Должно быть имя решателя, которое распознает pyomo, и это установлен, например «Глпк», «гуроби»
solver_options ( словарь ) — словарь с дополнительными параметрами, которые передаются решателю.(например, {‘thread’: 2} указывает gurobi использовать только 2 процессора)
solver_logfile ( None | string ) — Если не None, устанавливает параметр файла журнала решателя.
keep_files ( bool , по умолчанию False ) — сохранить файлы, которые pyomo создает из проблемы OPF строительство, например .lp файл — полезен для отладки
формулировка ( строка ) — Формулировка линейных уравнений потока мощности для использования; должно быть один из [«углы», «циклы», «кирхгоф», «ptdf»]
extra_functionality ( вызываемая функция ) — эта функция должна принимать два аргумента extra_functionality (сеть, снимки) и вызывается после построение модели завершено, но прежде, чем она будет отправлена в решатель.
 Это позволяет пользователю
добавить / изменить ограничения и добавить / изменить целевую функцию.
Это позволяет пользователю
добавить / изменить ограничения и добавить / изменить целевую функцию.ptdf_tolerance ( float ) — действует только тогда, когда pyomo имеет значение True. Значение, ниже которого записи PTDF игнорируются
free_memory ( установить , по умолчанию {‘pyomo’} ) — действует только тогда, когда pyomo имеет значение True. Любое подмножество {‘pypsa’, ‘pyomo’}. Позволяет хранить временной ряд pypsa данные на время работы решателя (как расслоение на диск) и / или бесплатно pyomo данные после извлечения раствора.
solver_io ( строка , по умолчанию Нет ) — действует только тогда, когда pyomo имеет значение True. Вариант ввода-вывода решателя, например «Питон» использовать «гуробипы» для solver_name = ”gurobi”
skip_pre ( bool , по умолчанию False ) — действует только тогда, когда pyomo имеет значение True.
 Пропустите предварительные шаги по вычислению топологии, вычисляя
зависимые значения и поиск управления шиной.
Пропустите предварительные шаги по вычислению топологии, вычисляя
зависимые значения и поиск управления шиной.extra_postprocessing (вызываемая функция ) — вступает в силу только тогда, когда pyomo имеет значение True. Эта функция должна принимать три аргумента extra_postprocessing (сеть, снимки, двойники) и вызывается после модель решена, и результаты извлечены. Это позволяет пользователю для получения дополнительной информации о решении, например, дополнительных теневые цены.
skip_objective ( bool , по умолчанию False ) — действует только тогда, когда pyomo имеет значение False.Пропустите запись целевой функции по умолчанию. Если False, пользовательский цель должна быть определена через extra_functionality.
warmstart ( bool или string , по умолчанию False ) — действует только тогда, когда pyomo имеет значение False.
 Используйте это, чтобы начать оптимизацию. Передайте строку, которая дает
путь к базовому файлу. Если установлено значение True, путь к
базовый файл должен быть указан в network.basis_fn.
Используйте это, чтобы начать оптимизацию. Передайте строку, которая дает
путь к базовому файлу. Если установлено значение True, путь к
базовый файл должен быть указан в network.basis_fn.store_basis ( bool , по умолчанию True ) — действует только тогда, когда pyomo имеет значение False.Сохранять ли основу результатов оптимизации. Если правда, путь к файлу базы сохраняется в network.basis_fn. Обратите внимание, что базис может быть сохранен только в симплексном, двойном симплексном или барьерном режимах. с кроссовером используется для решения.
keep_references ( bool , по умолчанию False ) — действует только тогда, когда pyomo имеет значение False. Сохраняйте ссылки на имена переменных и ограничений в сеть. Их можно найти в n.vars и n.cons после решения.
keep_shadowprices ( bool или список имен компонентов ) — вступает в силу только тогда, когда pyomo имеет значение False.
 Сохраните теневые цены для всех ограничений, если установлено значение True. Если список
передается, теневые цены будут анализироваться только для этого ограничения
имена. По умолчанию [«Автобус», «Линия», «GlobalConstraint»].
После решения теневые цены могут быть получены с помощью
Сохраните теневые цены для всех ограничений, если установлено значение True. Если список
передается, теневые цены будут анализироваться только для этого ограничения
имена. По умолчанию [«Автобус», «Линия», «GlobalConstraint»].
После решения теневые цены могут быть получены с помощью pypsa.linopt.get_dual ()с соответствующим именемsolver_dir ( str , по умолчанию Нет ) — действует только тогда, когда pyomo имеет значение False.Путь к каталогу, в который записаны необходимые файлы, по умолчанию Нет ведет во временный каталог по умолчанию, используемый tempfile.mkstemp ().
- Возвращает
status ( str ) — Статус оптимизации. Либо «хорошо», если решение оптимально, либо «предупреждение», если нет.
termination_condition ( str ) — Дополнительная информация о завершении работы решателя.
 Одно из «оптимальных», «неоптимальных» (в этом случае решение все еще остается
при условии), «недопустимый», «недопустимый или неограниченный» или «другое».
Одно из «оптимальных», «неоптимальных» (в этом случае решение все еще остается
при условии), «недопустимый», «недопустимый или неограниченный» или «другое».
Важно
Начиная с версии v0.16.0, PyPSA позволяет оптимизацию без использования pyomo, установив pyomo = False . Это делает работу lopf намного более эффективной с точки зрения использования памяти и времени. Для этого были введены два новых модуля: pypsa.linopf и pypsa.linopt , которые в основном отражают функциональность pypsa.opf и pypsa.opt , но без использования pyomo.Обратите внимание, что при установке для pyomo значения False extra_functionality необходимо адаптировать к соответствующему синтаксису (см. Рекомендации ниже). Некоторые функции привязки модулей еще не реализованы без pyomo.
Предупреждение
Если в пассивных сетях изменится пропускная способность, то сопротивление также изменится (т. Е. Если установлены параллельные линии). Это НЕ отражается в обычном LOPF, однако
Е. Если установлены параллельные линии). Это НЕ отражается в обычном LOPF, однако pypsa.linopf.ilopf покрывает это посредством итеративного процесса, как здесь.
Только оптимизация отгрузки — рыночная модель
Оптимизацию емкости можно отключить, чтобы оптимизирована, как модель краткосрочного рынка электроэнергии.
Для упрощенного представления передачи с использованием Net Transfer Емкости (NTC), есть компонент Link, который управляется поток энергии, как в транспортной модели (а также может представлять прямая связь HVDC).
Оптимизация общих годовых затрат на систему
Чтобы минимизировать долгосрочные годовые системные затраты для удовлетворения неэластичных электрических нагрузки, капитальные затраты на передачу и генерацию должны быть установлены на уровне годовые инвестиционные затраты в e.грамм. EUR / МВт / год, предельные затраты на отправка, например, EUR / MWh и весовые коэффициенты (теперь с единицами часов на annum, h / a) выбраны так, чтобы
\ [\ sum_t w_t = 8760 \]
В этом случае целевая функция дает общую стоимость системы в евро / год. чтобы соответствовать общей нагрузке.
чтобы соответствовать общей нагрузке.
Стохастическая оптимизация
Для простейшей стохастической оптимизации вы можете использовать
веса w_t как вероятности для снимков, которые могут
представляют различные нагрузки / погодные условия.Более сложный
функциональность планируется.
Переменные и сводка обозначений
\ (n \ in N = \ {0, \ dots | N | -1 \} \) | Маркировка автобусов |
\ (t \ in T = \ {0, \ dots | T | -1 \} \) | Обозначьте снимки |
\ (l \ in L = \ {0, \ dots | L | -1 \} \) | маркировка филиалов |
\ (s \ in S = \ {0, \ dots | S | -1 \} \) | Маркировка различных типов генератора / накопителя на каждой шине |
\ (w_t \) | взвешивание времени \ (t \) в целевой функции |
\ (g_ {n, s, t} \) | отправка генератора \ (s \) на автобусе \ (n \) в момент \ (t \) |
\ (\ bar {g} _ {n, s} \) | номинальная мощность генератора \ (s \) на шине \ (n \) |
\ (\ bar {g} _ {n, s, t} \) | наличие генератора \ (s \) на шине \ (n \) в момент \ (t \) на единицу номинальной мощности |
\ (u_ {n, s, t} \) | двоичная переменная состояния для генератора с привязкой блока |
\ (su_ {n, s, t} \) | стоимость запуска, если генератор с обязательством установки запускается во время \ (t \) |
\ (sdc_ {n, s, t} \) | Затраты на отключение, если генератор с обязательством установки отключен во время \ (t \) |
\ (c_ {n, s} \) | капитальные затраты на увеличение номинальной мощности генератора на 1 МВт |
\ (o_ {n, s} \) | предельная стоимость диспетчерского генератора за 1 МВтч |
\ (f_ {l, t} \) | поток мощности в ветви \ (l \) в момент \ (t \) |
\ (F_ {l} \) | емкость отделения \ (л \) |
\ (\ eta_ {n, s} \) | КПД генератора \ (s \) на шине \ (n \) |
\ (\ eta_ {l} \) | КПД регулируемого звена \ (л \) |
\ (e_s \) | Тонна эквивалента CO2 на МВтч топливовоза |
Дополнительные определения приведены ниже.
Целевая функция
См. pypsa.opf.define_linear_objective (сеть, снимки) .
Целевая функция состоит из капитальных затрат \ (c \) для каждого компонента и эксплуатационных затрат \ (o \) для генераторов
\ begin {gather *} \ sum_ {n, s} c_ {n, s} \ bar {g} _ {n, s} + \ sum_ {n, s} c_ {n, s} \ bar {h} _ {n, s} + \ sum_ {l} c_ {l} F_l \\ + \ sum_ {t} w_t \ left [\ sum_ {n, s} o_ {n, s, t} g_ {n, s, t} + \ sum_ {n, s} o_ {n, s, t} h_ {n, s, t} \ right] + \ sum_ {t} \ left [su_ {n, s, t} + sdc_ {n, s, t} \ right] \ end {gather *}
Дополнительные переменные, которые не фигурируют в целевой функции: переменная накопления, состояние заряда и угол напряжения для каждого автобуса.
Ограничения генератора
Они определены в pypsa.opf.define_generator_variables_constraints (сеть, снимки) .
Номинальная мощность генератора и диспетчеризация генератора для каждого снимка могут быть оптимизированы.
У каждого генератора есть переменная диспетчеризации \ (g_ {n, s, t} \), где \ (n \) обозначает шину, \ (s \) обозначает конкретный генератор в автобус (например, он может одновременно отображать ветряные / газовые / угольные генераторы автобус в агрегированной сети), а \ (t \) обозначает время.
Соответствует ограничениям:
\ [\ tilde {g} _ {n, s, t} * \ bar {g} _ {n, s} \ leq g_ {n, s, t} \ leq \ bar {g} _ {n, s, t} * \ bar {g} _ {n, s} \]
где \ (\ bar {g} _ {n, s} \) — номинальная мощность (генератор .p_ном )
и \ (\ tilde {g} _ {n, s, t} \) и \ (\ bar {g} _ {n, s, t} \) являются
временные ограничения на отправку (за единицу номинальной
мощность) из-за, например, наличие ветра или снижение номинальной мощности электростанции.
Для генераторов с изменяющимся во времени p_max_pu в сети .генераторы_т за единицу
доступность \ (\ bar {g} _ {n, s, t} \) — это временной ряд.
Для генераторов со статикой p_max_pu в сети . на единицу
доступность постоянна. Генераторы
Генераторы
Если номинальная мощность генератора \ (\ bar {g} _ {n, s} \) также является
предмет оптимизации ( generator.p_nom_extendable == True ) то
ограничения generator.p_nom_min и generator.p_nom_max на
также может быть введена устанавливаемая номинальная мощность, e.грамм.
\ [\ tilde {g} _ {n, s} \ leq \ bar {g} _ {n, s} \ leq \ hat {g} _ {n, s} \]
Ограничения обязательств генераторной установки
Они определены в pypsa.opf.define_generator_variables_constraints (сеть, снимки) .
Важно
Ограничения обязательств модуля будут построены полностью только в том случае, если для pyomo установлено значение True. Если для pyomo установлено значение False, упрощенная версия обязательства модуля рассчитывается путем игнорирования параметров min_up_time , min_down_time , start_up_cost , shut_down_cost , up_time_before и down_time_before .
Реализация является полной реализацией ограничений обязательств блока, определенных в главе 4.3 книги «Convex Optimization of Power Systems» Джошуа Адама Тейлора (CUP, 2015).
Принятие блока можно включить для любого генератора, установив для committable значение True . Это вводит
временный ряд новых двоичных переменных состояния \ (u_ {n, s, t} \ in \ {0,1 \} \), сохраненный в network.generators_t.status ,
который указывает, работает ли генератор (1) или нет (0) в
период \ (t \).Ограничения на мощность генератора теперь становятся:
\ [u_ {n, s, t} * \ tilde {g} _ {n, s, t} * \ bar {g} _ {n, s} \ leq g_ {n, s, t} \ leq u_ { n, s, t} * \ bar {g} _ {n, s, t} * \ bar {g} _ {n, s} \ hspace {.5cm} \ forall \, n, s, t \]
, так что если \ (u_ {n, s, t} = 0 \), то также \ (g_ {n, s, t} = 0 \).
Обратите внимание, что генератор не может быть одновременно расширяемым ( generator.p_nom_extendable == True ) и фиксируемым ( generator.) из-за связи переменных \ (u_ {n, s, t} \)
и \ (\ bar {g} _ {n, s} \) здесь.{t + T_ \ textrm {min_up}} u_ {n, s, t ‘} \ geq T_ \ textrm {min_up} (u_ {n, s, t} — u_ {n, s, t-1}) \ hspace {.5cm} \ forall \, n, s, t \] committable == True
committable == True
, т.е. если генератор только что запустился в момент \ (t \), то \ (u_ {n, s, t-1} = 0 \), \ (u_ {n, s, t} = 1 \) и \ (u_ {n, s, t} — u_ {n, s, t-1} = 1 \), так что он должен работать не менее \ (T _ {\ textrm {min_up}} \) периодов.
Генератор мог быть включен в течение некоторых периодов перед периодом моделирования снимков . Если время безотказной работы до запуска снимков меньше минимального времени безотказной работы, то генератор вынужден работать с учетом разницы в начале снимков .Если начало снимков — это начало network.snapshots , то время работы перед симуляцией считывается из входной переменной generator.up_time_before . Если снимков попадает в середину network., тогда PyPSA принимает статусы на несколько часов до того, как 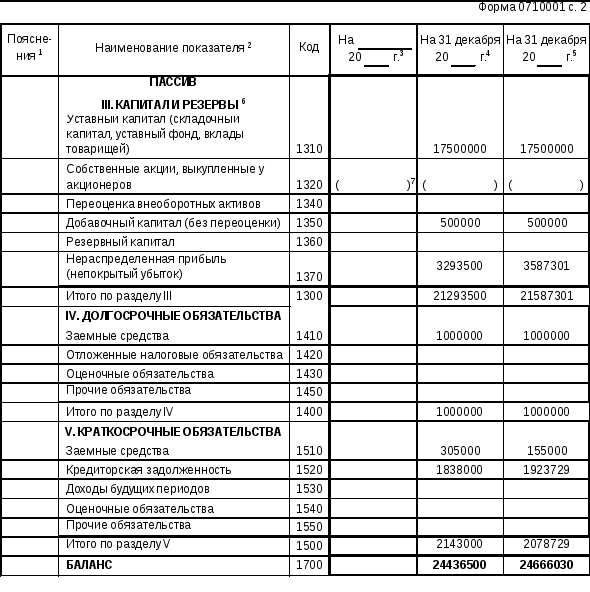 snapshots
snapshots снимков были установлены предыдущими симуляциями, и считывает предыдущее время работоспособности, исследуя предыдущие статусы. Если начало снимков очень близко к началу сети .{t + T_ \ textrm {min_down}} (1-u_ {n, s, t '}) \ geq T_ \ textrm {min_down} (u_ {n, s, t-1} - u_ {n, s, t }) \ hspace {.5cm} \ forall \, n, s, t \]
Вы также можете определить generator.down_time_before для периодов до network.snapshots , аналогично времени работы.
Для ненулевых начальных затрат \ (success_ {n, s} \) новая переменная \ (success_ {n, s, t} \ geq 0 \) вводится для каждого периода времени \ (t \) и добавляется к целевая функция. Переменная удовлетворяет
\ [success_ {n, s, t} \ geq success_ {n, s} (u_ {n, s, t} - u_ {n, s, t-1}) \ hspace {.5см} \ forall \, n, s, t \]
, так что он не равен нулю, только если \ (u_ {n, s, t} - u_ {n, s, t-1} = 1 \), т.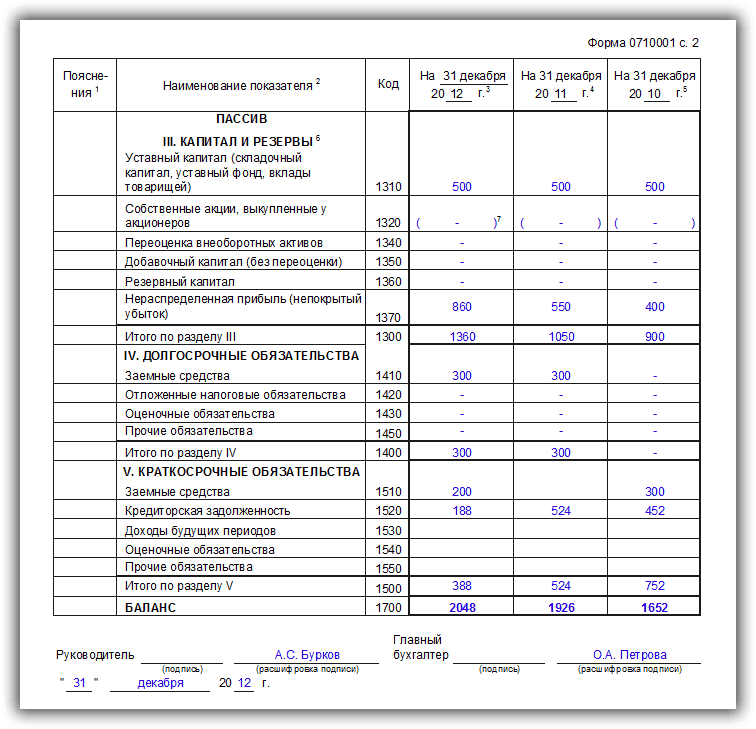 е. генератор только что запущен, и в этом случае неравенство насыщается \ (успех_ {п, с, т} = успех_ {п, с} \). Аналогично для затрат на отключение \ (sdc_ {n, s, t} \ geq 0 \) у нас есть
е. генератор только что запущен, и в этом случае неравенство насыщается \ (успех_ {п, с, т} = успех_ {п, с} \). Аналогично для затрат на отключение \ (sdc_ {n, s, t} \ geq 0 \) у нас есть
\ [sdc_ {n, s, t} \ geq sdc_ {n, s} (u_ {n, s, t-1} - u_ {n, s, t}) \ hspace {.5cm} \ forall \, n , с, т \]
Ограничения линейного изменения генератора
Они определены в pypsa.opf.define_generator_variables_constraints (сеть, снимки) .
Реализация соответствует главе 4.3 Convex Optimization of Power Systems. Джошуа Адам Тейлор (КУБОК, 2015).
Пределы скорости изменения могут быть определены для увеличения выходной мощности \ (ru_ {n, s} \) и уменьшение выходной мощности \ (rd_ {n, s} \). От по умолчанию они равны нулю и игнорируются. Их следует давать на единицу номинальная мощность генератора. Отправка генератора подчиняется
.\ [- rd_ {n, s} * \ bar {g} _ {n, s} \ leq (g_ {n, s, t} - g_ {n, s, t-1}) \ leq ru_ {n, s} * \ bar {g} _ {n, s} \]
для \ (t \ in \ {1, \ dots | T | -1 \} \).
Для генераторов с обязательством установки вы также можете указать пределы рампы. при запуске \ (rusu_ {n, s} \) и остановке \ (rdsd_ {n, s} \)
\ begin {gather *} \ left [-rd_ {n, s} * u_ {n, s, t} -rdsd_ {n, s} (u_ {n, s, t-1} - u_ {n, s, t}) \ right] \ bar {g} _ {n, s} \\ \ leq (g_ {n, s, t} - g_ {n, s, t-1}) \ leq \\ \ left [ru_ {n, s} * u_ {n, s, t-1} + rusu_ {n, s} (u_ {n, s, t} - u_ {n, s, t-1}) \ right ] \ bar {g} _ {n, s} \ end {gather *}
Ограничения единицы хранения
Они определены в pypsa.opf.define_storage_variables_constraints (сеть, снимки) .
Номинальная мощность хранилища и отправка для каждого снимка могут быть оптимизированы.
С блоком хранения максимальное состояние заряда не может быть оптимизировано независимо от максимальной выходной мощности (они связаны с переменной максимальной продолжительностью работы), а максимальная выходная мощность связана с максимальной потребляемой мощностью. Чтобы оптимизировать эти емкости независимо, создайте единицу хранения из более фундаментальных компонентов Store и Link .
Номинальная мощность накопителя определяется как \ (\ bar {h} _ {n, s} \).
В отличие от генератора, который имеет одну зависящую от времени переменную, в каждом блоке хранения их три:
Отправка хранилища \ (h_ {n, s, t} \) (когда оно истощает состояние заряда):
\ [0 \ leq h_ {n, s, t} \ leq \ bar {h} _ {n, s} \]
Потребление памяти \ (f_ {n, s, t} \) (когда увеличивается уровень заряда):
\ [0 \ leq f_ {n, s, t} \ leq \ bar {h} _ {n, s} \]
и само состояние заряда:
\ [0 \ leq soc_ {n, s, t} \ leq r_ {n, s} \ bar {h} _ {n, s} \]
где \ (r_ {n, s} \) - количество часов при номинальной мощности, которые заполняют состояние заряда.{-1} _ {\ textrm {dispatch}; n, s} w_t h_ {n, s, t} + w_t \ textrm {inflow} _ {n, s, t} - w_t \ textrm {spillage} _ {n , s, t} \]
\ (\ eta _ {\ textrm {stand}; n, s} \) - задолженность по постоянным убыткам
например тепловые потери на тепловые
место хранения. \ (\ eta _ {\ textrm {store}; n, s} \) и
\ (\ eta _ {\ textrm {dispatch}; n, s} \) - потери эффективности для
мощность, входящая и выходящая из блока хранения.
Есть два варианта указания начального состояния заряда \ (soc_ {n, s, t = -1} \): вы можете установить storage_unit.cyclic_state_of_charge = False (по умолчанию) и значение Storage_unit.state_of_charge_initial в МВтч; или вы можете установить storage_unit.cyclic_state_of_charge = True , а затем
оптимизация предполагает \ (soc_ {n, s, t = -1} = soc_ {n, s, t = | T | -1} \).
Если во временном ряду storage_unit_t.state_of_charge_set есть
значения, которые не являются NaN, тогда предполагается, что они
фиксированное состояние зарядов, желаемое для этого времени \ (t \), и они будут
быть добавленными как дополнительные ограничения. (Возможный вариант использования:
Единица хранения, где состояние заряда должно опустошаться каждый день.)
Ограничения магазина
Они определены в pypsa.opf.define_store_variables_constraints (сеть, снимки) .
Сохранение номинальной энергии и рассылка для каждого снимка может быть оптимизирована. {w_t} e_ {n, s, t-1} - w_t h_ {n, s, t} \]
{w_t} e_ {n, s, t-1} - w_t h_ {n, s, t} \]
\ (\ eta _ {\ textrm {stand}; n, s} \) - задолженность по постоянным убыткам е.грамм. тепловые потери на тепловые место хранения.
Есть два варианта указания начальной энергии
\ (e_ {n, s, t = -1} \): вы можете установить store.e_cyclic = False (по умолчанию) и
значение store.e_initial в МВтч; или вы можете
установите store.e_cyclic = True , а затем
оптимизация предполагает \ (e_ {n, s, t = -1} = e_ {n, s, t = | T | -1} \).
Пассивные ответвления: линии и трансформаторы
См. pypsa.opf.define_passive_branch_flows (сеть, снимки) и pypsa.opf.define_passive_branch_constraints (сеть, снимки) и pypsa.opf.define_branch_extension_variables (сеть, снимки) .
Для линий и трансформаторов, мощность которых течет в соответствии с полным сопротивлением, поток мощности \ (f_ {l, t} \) в сетях переменного тока определяется разностью напряжений углы \ (\ theta_ {n, t} \) на шине 0 и \ (\ theta_ {m, t} \) на шине 1, деленные на последовательное реактивное сопротивление \ (x_l \)
\ [f_ {l, t} = \ frac {\ theta_ {n, t} - \ theta_ {m, t}} {x_l} \]
(Для сетей постоянного тока замените углы напряжения разницей в величине напряжения \ (\ delta V_ {n, t} \) и последовательное реактивное сопротивление последовательным сопротивлением \ (r_l \). )
)
Этот поток ограничен емкостью: math: F_l строки
\ [| f_ {l, t} | \ leq F_l \]
Примечание
Если \ (F_l \) также подлежит оптимизации
( branch.s_nom_extendable - Истина ), тогда полное сопротивление \ (x \)
линия НЕ изменяется автоматически вместе с емкостью (для представления
например добавляются параллельные линии).
Здесь есть два варианта:
Повторите LOPF еще раз с обновленными импедансами, см. E.грамм. http://www.sciencedirect.com/science/article/pii/S0360544214000322#, как это сделано
pypsa.linopf.ilopfJoão Gorenstein Dedecca также реализовал MILP-версию расширения передачи, см. Https://github.com/jdedecca/MILP_PyPSA, которая должным образом учитывает импеданс с дизъюнктивной релаксацией. Скоро это будет добавлено в основную базу кода PyPSA.
Составы для пассивного ответвления потока
PyPSA реализует четыре формулировки линейных уравнений потока мощности. которые математически эквивалентны, но могут иметь разные время решения.Эти различные составы описаны и протестировано в препринте arXiv Linear Optimal Power Flow Using Цикл потоков.
Вы можете выбрать формулировку, передав network.lopf в
аргумент формулировка , который должен быть в [«углы», «циклы», «кирхгоф», «птдф»] .
углов- это стандартные формулы, основанные на описанных выше углах напряжения, используемые для линейного потока мощности и встречающиеся в учебниках.ptdfиспользует формулировку коэффициента распределения передачи мощности (PTDF), которую можно найти, например, в http: // www.sciencedirect.com/science/article/pii/S0360544214000322#.kirchhoffициклы- это две новые формулировки, основанные на теоретико-графическом разложении сетевых потоков на остовное дерево и замкнутые циклы.
На основе эталонного тестирования в цикле использования линейного оптимального потока мощности
Потоки для стандартных сетей, kirchhoff почти всегда решает быстрее всех, в среднем в 3 раза быстрее
чем формула angles и до 20 раз быстрее в конкретных
случаи.Ускорение выше для больших сетей с диспетчеризацией.
генераторы на большинстве узлов.
Управляемые ответвления: ссылки
См. pypsa.opf.define_controllable_branch_flows (сеть, снимки) и pypsa.opf.define_branch_extension_variables (сеть, снимки) .
Для каналов, поток мощности которых является управляемым, существует просто переменная оптимизации для каждого компонента, удовлетворяющая
\ [| f_ {l, t} | \ leq F_l \]
Если поток ссылок положительный \ (f_ {l, t}> 0 \), то он удаляется
\ (f_ {l, t} \) от bus0 и подает в \ (\ eta_l f_ {l, t} \) на bus1 , где \ (\ eta_l \) - эффективность канала.
Если дополнительные выходные шины busi для \ (i = 2,3, \ dots \) являются
определены (например, bus2 , bus3 и т. д.) и связанные с ними
КПД КПД , т.е. \ (\ eta_ {i, l} \), то при busi подача - \ (\ eta_ {i, l} f_ {l, t} \). Смотрите также
Связь с несколькими выходами или входами.
Узловые силовые балки
См. pypsa.opf.define_nodal_balances (сеть, снимки) .
Это наиболее важное уравнение, которое гарантирует, что мощность балансирует на каждой шине \ (n \) за каждый момент времени \ (t \).
\ [\ sum_ {s} g_ {n, s, t} + \ sum_ {s} h_ {n, s, t} - \ sum_ {s} f_ {n, s, t} - \ sum_ {l} K_ {nl} f_ {l, t} = \ sum_ {s} d_ {n, s, t} \ hspace {.4cm} \ leftrightarrow \ hspace {.4cm} w_t \ lambda_ {n, t} \]
Где \ (d_ {n, s, t} \) - экзогенная нагрузка в каждом узле ( load.p_set ), а матрица инцидентности \ (K_ {nl} \) для графика принимает значения в \ (\ { -1,0,1 \} \) в зависимости от того, заканчивается ветка \ (l \) или начинается у автобуса. \ (\ lambda_ {n, t} \) - теневая цена ограничения, то есть предельная цена местоположения, хранящаяся в сети .bus_t.marginal_price .
Роль автобуса - обеспечить энергосбережение для всех элементов. подпитывает его (то есть, как Текущий закон Кирхгофа).
Глобальные ограничения
См. pypsa.opf.define_global_constraints (сеть, снимки) .
Глобальные ограничения применяются более чем к одному компоненту.
В настоящее время определены только ограничения «первичной энергии». Они зависят от эффективности электростанции и специфических для оператора атрибутов, таких как удельные выбросы CO2.
Предположим, что существует глобальное ограничение, определенное для выбросов CO2 с
смысл <= и константа \ textrm {CAP} _ {CO2} . Выбросы могут прийти
от генераторов, энергоносители которых имеют выбросы CO2, и от
склады и единицы хранения, среда хранения которых выделяет или поглощает CO2
когда он конвертируется. Только магазины и блоки хранения с нециклическими
состояние заряда, которое различается в начале и в конце
моделирование может внести свой вклад.
Если удельные выбросы энергоносителя \ (s \) равны \ (e_s \)
( перевозчик.co2_emissions ) Тонна-эквивалента CO2 на МВтч и
генератор с носителем \ (s \) в узле \ (n \) имеет КПД
\ (\ eta_ {n, s} \) тогда ограничение CO2 равно
\ [\ sum_ {n, s, t} \ frac {1} {\ eta_ {n, s}} w_t \ cdot g_ {n, s, t} \ cdot e_ {n, s} + \ sum_ {n, s} \ left (e_ {n, s, t = -1} - e_ {n, s, t = | T | -1} \ right) \ cdot e_ {n, s} \ leq \ textrm {CAP} _ {CO2} \ hspace {.4cm} \ leftrightarrow \ hspace {.4cm} \ mu \]
Первая сумма сверх генераторов; вторая сумма больше магазинов и
единицы хранения. \ (\ mu \) - теневая цена ограничения,
я.е. цена СО2 в этом случае. \ (\ mu \) является выходом
оптимизация хранится в network.global_constraints.mu .
Пользовательские ограничения и другие функции
Начиная с PyPSA v0.16.0, функция lopf предоставляется двумя разными модулями. Обычная реализация на основе модуля pypsa.opf использует
pyomo для постановки задачи линейной оптимизации и передачи ее решателю. Реализация без pyomo, основанная на модуле pypsa.linopf , использует прямой подход для записи .lp напрямую и явно запустив его из интерфейса решателя. Поэтому применение настраиваемых ограничений зависит от того, активирован ли pyomo или нет.
Обычно для пользовательского ограничения передайте функцию network.lopf a
функция extra_function в качестве аргумента. Эта функция должна
взять два аргумента extra_functionality (сеть, снимки) и
вызывается после завершения построения модели, но перед отправкой в
решатель.Это позволяет пользователю добавлять, изменять или удалять ограничения.
и изменить целевую функцию.
1. Для pyomo установлено значение True
Вы легко можете расширить задачу оптимизации, построенную PyPSA, используя обычные синтаксис pyomo.
Пример ТЭЦ и
пример, который заменяет генераторы и блоки хранения фундаментальными связями
и магазины
оба передают аргумент extra_functionality в LOPF, чтобы добавить
функциональность.
Функция extra_postprocessing вызывается после того, как модель
решено, и результаты извлечены.Эта функция должна занимать три
аргументы extra_postprocessing (сеть, снимки, двойники) . Это позволяет
пользователь может извлечь дополнительную информацию о решении, например
дополнительные теневые цены за ограничения.
2. Pyomo имеет значение False
Обычно, когда pyomo отключен, все ссылки на переменные и ограничения хранятся в самом сетевом объекте. Таким образом, каждая переменная и ограничение привязаны к компоненту, например диспетчерская переменная network.generators.p прикреплен к компоненту «Генератор» и может быть легко доступен с
>>> get_var (n, 'Генератор', 'p')
Дополнительное ограничение может быть легко реализовано с помощью функций
pypsa.linopt.get_varдля получения переменных, которые должны быть включены в ограничениеpypsa.linopt.linexprдля создания линейных выражений для левой части (lhs) ограничения. Обратите внимание, что только lhs включает все термины с переменными, rhs является константой.pypsa.linopt.define_constraintsдля определения сетевого ограничения.
Функции определены как таковые:
- linopt.get_var ( c , attr , pop = False )
Извлекает ссылки на переменные для заданного статического или зависящего от времени атрибут данного компонента. Функция просматривает n. Переменных, чтобы определить, является ли переменная зависящей от времени или статической.
- Параметры
н ( pypsa.Сеть ) -
c ( str ) - имя компонента, которому принадлежит ограничение
attr ( str ) - имя атрибута ограничений
Пример
>>> get_var (n, 'Генератор', 'p')
- linopt.linexpr ( * , as_pandas = True , return_axes = False )
Поэлементное объединение кортежей в форме (коэффициент, переменные).Коэффициенты и переменные могут быть массивами, сериями или кадрами. По умолчанию возвращает pandas.Series или pandas.DataFrame строк. Если return_axes установлен на True, возвращаемое значение разбивается на значения и оси, где значения являются numpy.array и осями кортежа, содержащего индекс и столбец, если они есть.
- Параметры
кортежа ( кортежа ) -
Каждый кортеж должен иметь форму (coeff, var), где
coeff - числовое значение или числовой массив, серия, кадр
var - строка или массив, серия, фрейм переменных строк
as_pandas ( bool , по умолчанию True ) - следует ли возвращаться к результирующему массиву в виде серии, если он одномерный, или каркас, если 2-х мерный.Заменяет аргумент return_axes.
return_axes ( Boolean , по умолчанию False ) - следует ли возвращать индекс и столбец (если они существуют)
Пример
Инициализировать коэффициенты и переменные
>>> coeff1 = 1 >>> var1 = pd.Series (['a1', 'a2', 'a3']) >>> coeff2 = pd.Series ([- 0,5, -0,3, -1]) >>> var2 = pd.Series (['b1', 'b2', 'b3'])
Создание строк линейного выражения
>>> linexpr ((coeff1, var1), (coeff2, var2)) 0 +1.0 a1 -0,5 b1 1 +1,0 a2 -0,3 b2 2 +1,0 a3 -1,0 b3 dtype: объект
Для следующего шага полученный кадр можно использовать как левую часть
pypsa.linopt.define_constraints ()Для получения только значений:
>>> linexpr ((coeff1, var1), (coeff2, var2), as_pandas = False) array (['+ 1.0 a1 -0.5 b1', '+1.0 a2 -0.3 b2', '+1.0 a3 -1.0 b3'], dtype = объект)
- linopt.define_constraints ( lhs , sense , rhs , name , attr = '' , axes = None , spec = '' )
Определяет ограничение (я) для pypsa-сети с заданной левой стороной (lhs), смысл и правая часть (правая сторона).Ограничения хранятся в сети. объект под n.cons с ключом имени ограничения. Если несколько ограничений определены в единицах, только с использованием np.arrays, тогда можно использовать аргумент axes для определения осей ограничений (особенно рекомендуется для зависящих от времени ограничений). Если один из lhs, sense и rhs является pd.Series / pd.DataFrame аргумент оси не нужен.
- Параметры
н ( pypsa.Сеть ) -
левый ( pd.Series / pd.DataFrame / np.array / str / float ) - левая часть ограничений, созданных с помощью
pypsa.linot.linexpr ().смысл ( pd.Series / pd.DataFrame / np.array / str / float ) - смысл (я) ограничения (я)
rhs ( pd.Series / pd.DataFrame / np.array / str / float ) - правая часть ограничения (ограничений), должна содержать только чистые константы, без переменных
имя ( str ) -
общее имя ограничения (или компонента, который является ограничением ссылаясь на).После этого ограничение будет сохранено в:
.attr ( str default '' ) - Указание имени ограничения, определяет, под каким именем ограничения хранятся в n.cons [name] .pnl, если они двумерные или в n.cons [имя] .df, если одномерный
оси ( pd.Index или кортеж объектов pd.Index , по умолчанию Нет ) - задает оси, если все lhs, sense и rhs равны np.массивы или одиночные струны или поплавки.
Пример
Допустим, мы хотим ограничить все газовые генераторы максимальной мощностью 100 МВтч. во время первых 10 снимков. Затем мы сначала получаем все операционные переменные для этого подмножества и ограничения сумма меньше 100.
>>> из pypsa.linopt import get_var, linexpr, define_constraints >>> gas_i = n.generators.query ('carrier == "Natural Gas"'). index >>> gas_vars = get_var (n, 'Генератор', 'p').loc [n.snapshots [: 10], gas_i] >>> lhs = linexpr ((1, gas_vars)). sum (). sum () >>> define_ (n, lhs, '<=', 100, 'Generator', 'gas_power_limit')Теперь ссылки на ограничения доступны по
pypsa.linopt.get_con ()с использованием>>> cons = get_var (n, 'Генератор', 'gas_power_limit')
Под капотом они хранятся в n.cons.Generator.pnl.gas_power_limit. Для получения их теневых цен добавьте общее имя ограничения аргументу keep_shadowprices.
Обратите внимание, что это полезно для аргумента extra_functionality .
Функция extra_postprocessing не требуется, если pyomo отключен. Для получения дополнительных теневых цен просто передайте имя ограничения, к которому оно привязано, в параметр keep_shadowprices функции lopf .
Входы
Для оптимального линейного потока мощности следующие данные для каждого компонента используются.Почти для всех значений используются значения по умолчанию, если не явно установлен. Для значений по умолчанию и единиц измерения см. Компоненты.
- сеть
. {Snapshot_weightings}
автобус. {V_nom, carrier}
нагрузка. {P_set}
- Генератор
. {P_nom, p_nom_extendable, p_nom_min, p_nom_max, p_min_pu, p_max_pu, marginal_cost, capital_cost, efficiency, carrier}
storage_unit. {P_nom, p_nom_extendable, p_nom_min, p_nom_max, p_min_pu, p_max_pu, marginal_cost, capital_cost, efficiency *, постоянные_потери, приток, state_of_charge_set, max_hours_16}
магазин.{e_nom, e_nom_extendable, e_nom_min, e_nom_max, e_min_pu, e_max_pu, e_cyclic, e_initial, capital_cost, marginal_cost, Standing_loss}
строка. {X, s_nom, s_nom_extendable, s_nom_min, s_nom_max, capital_cost}
трансформатор. {X, s_nom, s_nom_extendable, s_nom_min, s_nom_max, capital_cost}
ссылка. {P_min_pu, p_max_pu, p_nom, p_nom_extendable, p_nom_min, p_nom_max, capital_cost}
оператор связи. {Carrier_attribute}
global_constraint.{type, carrier_attribute, sense, constant}
Примечание
Обратите внимание, что для линий и трансформаторов вы ДОЛЖНЫ убедиться, что \ (x \) не равно нулю, иначе матрица проводимости шины будет сингулярной.
Выходы
автобус. {V_mag_pu, v_ang, p, marginal_price}
груз. {П}
- Генератор
. {P, p_nom_opt}
storage_unit. {P, p_nom_opt, state_of_charge, spill}
магазин.{p, e_nom_opt, e}
строка. {P0, p1, s_nom_opt, mu_lower, mu_upper}
трансформатор. {P0, p1, s_nom_opt, mu_lower, mu_upper}
ссылка. {P0, p1, p_nom_opt, mu_lower, mu_upper}
global_constraint. {Mu}
Служебные функции (без pyomo)
Предупреждение
В будущих версиях документации они будут перечислены исключительно в Справочнике по API.
Сборка задач оптимизации из сетей PyPSA без Pyomo.Первоначально заимствовано из nomopyomo (-> «no more Pyomo»).
- pypsa.linopf.assign_solution ( n , sns , variables_sol , constraints_dual , keep_references = False , keep_shadowprices = None )
Вспомогательная функция. Назначает решение успешной оптимизации сеть.
- pypsa.linopf.define_dispatch_for_extendable_and_committable_variables ( n , sns , c , attr )
Инициализирует переменные для распределения мощности для данного компонента и данный атрибут.
- Параметры
н ( pypsa.Сеть ) -
c ( str ) - имя компонента сети
attr ( str ) - имя атрибута, например ‘P’
- pypsa.linopf.define_dispatch_for_extendable_constraints ( n , sns , c , attr )
Устанавливает ограничения распределения мощности для расширяемых устройств для заданного компонент и заданный атрибут.
- Параметры
н ( pypsa.Сеть ) -
c ( str ) - имя компонента сети
attr ( str ) - имя атрибута, например ‘P’
- pypsa.linopf.define_dispatch_for_non_extendable_variables ( n , sns , c , attr )
Инициализирует переменные для распределения мощности для данного компонента и данный атрибут.
- Параметры
н ( pypsa.Сеть ) -
c ( str ) - имя компонента сети
attr ( str ) - имя атрибута, например ‘P’
- pypsa.linopf.define_fixed_variable_constraints ( n , sns , c , attr , pnl = True )
Устанавливает ограничения для фиксации переменных данного компонента и атрибута к соответствующим значениям в n.df (c) [attr + ‘_set’], если pnl имеет значение True, или n.pnl (c) [attr + ‘_set’]
- Параметры
н ( pypsa.Сеть ) -
c ( str ) - имя компонента сети
attr ( str ) - имя атрибута, например ‘P’
pnl ( bool , по умолчанию True ) - зависит ли переменная, которая должна быть фиксированной, от времени
- pypsa.linopf.define_global_constraints ( n , sns )
Определяет глобальные ограничения для оптимизации. Возможные типы:
- primary_energy
Используйте это, чтобы ограничить побочные продукты первичных источников энергии как CO2
- Transmission_volume_expansion_limit
Используйте это, чтобы установить предел для увеличения объема линии. Возможные перевозчики "AC" и "DC"
- Transmission_expansion_cost_limit
Используйте это, чтобы установить предел затрат на расширение линии.Возможные перевозчики "AC" и "DC"
- pypsa.linopf.define_kirchhoff_constraints ( n , sns )
Определяет ограничения напряжения Кирхгофа
- pypsa.linopf.define_nodal_balance_constraints ( n , sns )
Определяет узловое ограничение баланса.
- pypsa.linopf.define_nominal_for_extendable_variables ( n , c , attr )
Инициализирует переменные номинальной мощности для данного компонента и данный атрибут.
- Параметры
н ( pypsa.Сеть ) -
c ( str ) - сетевой компонент, номинальная мощность которого должна быть определена
attr ( str ) - имя переменной, например «П_ном»
- pypsa.linopf.define_objective ( n , sns )
Определяет и записывает целевую функцию
- pypsa.linopf.define_ramp_limit_constraints ( n , sns )
Определяет пределы рампы для генераторов с допустимым пределом рампы
- pypsa.linopf.define_storage_unit_constraints ( n , sns )
Определяет ограничения состояния заряда (soc) для единиц хранения. В принципе состояния ограничений:
previous_soc + p_store - p_dispatch + inflow - spill == soc
- pypsa.linopf.define_store_constraints ( n , sns )
Определяет ограничения энергетического баланса для магазинов. В основном это означает:
- pypsa.linopf.ilopf ( n , снимков = Нет , msq_threshold = 0,05 , min_iterations = 1 , max_iterations = 100 , track_iterations = False , ** kwargs )
Итеративная линейная оптимизация, обновляющая параметры линии для пассивной Линии переменного и постоянного тока.Это полезно, когда включено расширение линии. После каждого Успешное решение, пересчитываются импедансы и сопротивление линии на основе результата оптимизации. Если теплый старт возможен, он использует результат предыдущей итерации, чтобы ускорить оптимизацию.
- Параметры
снимков ( список или индексный фрагмент ) - список снимков для оптимизации, должен быть подмножеством network.snapshots, по умолчанию network.снимки
msq_threshold ( float , по умолчанию 0,05 ) - максимальная среднеквадратичная разница между оптимизированной пропускной способностью линии текущая и предыдущая итерации. Как только этот порог станет undercut, и количество итераций больше, чем min_iterations итерационная оптимизация останавливается
min_iterations ( целое , по умолчанию 1 ) - Минимальное количество итераций для запуска независимо от того, установлен ли msq_threshold уже подрезан
max_iterations ( целое , по умолчанию 100 ) - максимальное количество итераций для запуска независимо от того, является ли msq_threshold уже подрезан
track_iterations ( bool , по умолчанию False ) - если True, пропускная способность промежуточных ветвей и значения целевая функция записывается для каждой итерации.Ценности итерация 0 представляет начальное состояние.
** kwargs - аргументы ключевого слова функции lopf, которая выполняется на каждой итерации
- pypsa.linopf.network_lopf ( n , моментальных снимков = Нет , solver_name = 'cbc' , solver_logfile = Нет , extra_functionality = Нет , skip_objective = False , skip_process = False = Нет , формулировка = 'kirchhoff' , keep_references = False , keep_files = False , keep_shadowprices = ['Bus', 'Line', 'Transformer', 'Link', 'GlobalConstraint'] , solver_options = Нет , теплый старт = Ложь , store_basis = Ложь , solver_dir = Нет )
Линейный оптимальный поток мощности для группы снимков.
- Параметры
снимков ( список или индексный фрагмент ) - список снимков для оптимизации, должен быть подмножеством network.snapshots, по умолчанию network.snapshots
solver_name ( string ) - Должно быть имя решателя, которое распознает pyomo, и это установлен, например «Глпк», «гуроби»
solver_logfile ( None | string ) - Если не None, устанавливает параметр файла журнала решателя.
solver_options ( словарь ) - словарь с дополнительными параметрами, которые передаются решателю. (например, {‘thread’: 2} указывает gurobi использовать только 2 процессора)
solver_dir ( str , default None ) - Путь к каталогу, в который записаны необходимые файлы, по умолчанию None ведет во временный каталог по умолчанию, используемый tempfile.mkstemp ().
keep_files ( bool , по умолчанию False ) - сохранить файлы, которые pyomo создает из проблемы OPF строительство, e.грамм. .lp файл - полезен для отладки
формулировка ( строка ) - Формулировка линейных уравнений потока мощности для использования; должно быть один из [«углы», «циклы», «кирхгоф», «ptdf»]
extra_functionality ( вызываемая функция ) - эта функция должна принимать два аргумента extra_functionality (сеть, снимки) и вызывается после построение модели завершено, но прежде, чем она будет отправлена в решатель. Это позволяет пользователю добавить / изменить ограничения и добавить / изменить целевую функцию.
skip_pre ( bool , по умолчанию False ) - пропустить предварительные шаги по вычислению топологии.
skip_objective ( bool , по умолчанию False ) - пропустить запись целевой функции по умолчанию. Если False, пользовательский цель должна быть определена через extra_functionality.
extra_postprocessing (вызываемая функция ) - эта функция должна принимать три аргумента extra_postprocessing (сеть, снимки, двойники) и вызывается после модель решена, и результаты извлечены.Это позволяет пользователю для получения дополнительной информации о решении, например, дополнительных теневые цены.
теплый старт ( bool или строка , по умолчанию Ложь ) - используйте это для горячего старта оптимизации. Передайте строку, которая дает путь к базовому файлу. Если установлено значение True, путь к базовый файл должен быть указан в network.basis_fn.
store_basis ( bool , по умолчанию False ) - следует ли сохранять основу результатов оптимизации.Если правда, путь к файлу базы сохраняется в network.basis_fn. Обратите внимание, что базис может быть сохранен только в симплексном, двойном симплексном или барьерном режимах. с кроссовером используется для решения.
keep_references ( bool , по умолчанию False ) - сохранять ссылки на имена переменных и ограничений в сеть. Их можно найти в n.vars и n.cons после решения.
keep_shadowprices ( bool или список имен компонентов ) - Сохранять теневые цены для всех ограничений, если установлено значение True.Если список передается, теневые цены будут анализироваться только для этого ограничения имена. По умолчанию [«Автобус», «Линия», «GlobalConstraint»]. После решения теневые цены могут быть получены с помощью
pypsa.linopt.get_dual ()с соответствующим именем
- pypsa.linopf.prepare_lopf ( n , снимков = Нет , keep_files = Ложь , skip_objective = Ложь , extra_functionality = Нет , solver_dir = Нет )
Устанавливает линейную задачу и записывает ее в файл lp.
- Возврат
Служебные функции (с pyomo)
Предупреждение
В будущих версиях документации они будут перечислены исключительно в Справочнике по API.
Оптимальные функции потока мощности.
- pypsa.opf.define_nodal_balances (сеть , снимки )
Построить узловой баланс для всех элементов, кроме пассивного. ветви.
Сохранение узлового выражения баланса в сети._p_balance.
- pypsa.opf.define_passive_branch_flows_with_kirchhoff (сеть , снимки , skip_vars = False )
определить пассивные ветвления с помощью метода Кирхгофа
- pypsa.opf.define_sub_network_cycle_constraints ( подсеть , снимки , passive_branch_p , атрибут )
Создает cycle_constraints для конкретной подсети
- pypsa.opf.network_lopf ( network , snapshots = None , solver_name = 'glpk' , solver_io = None , skip_pre = False , extra_functionality = None , solver_logfile = None o, solver_logfile = None o, {solver } , keep_files = False , формулировка = 'углы' , ptdf_tolerance = 0,0 , free_memory = {} , extra_postprocessing = Нет )
Линейный оптимальный поток мощности для группы снимков.
- Параметры
снимков ( список или индексный фрагмент ) - список снимков для оптимизации, должен быть подмножеством network.snapshots, по умолчанию network.snapshots
solver_name ( string ) - Должно быть имя решателя, которое распознает pyomo, и это установлен, например «Глпк», «гуроби»
solver_io ( строка , по умолчанию Нет ) - параметр ввода-вывода решателя, e.грамм. «Питон» использовать «гуробипы» для solver_name = ”gurobi”
skip_pre ( bool , по умолчанию False ) - пропустить предварительные шаги вычисления топологии, вычисления зависимые значения и поиск управления шиной.
extra_functionality ( вызываемая функция ) - эта функция должна принимать два аргумента extra_functionality (сеть, снимки) и вызывается после построение модели завершено, но прежде, чем она будет отправлена в решатель.Это позволяет пользователю добавить / изменить ограничения и добавить / изменить целевую функцию.
solver_logfile ( None | string ) - Если не None, устанавливает параметр файла журнала решателя.
solver_options ( словарь ) - словарь с дополнительными параметрами, которые передаются решателю. (например, {‘thread’: 2} указывает gurobi использовать только 2 процессора)
keep_files ( bool , по умолчанию False ) - сохранить файлы, которые pyomo создает из проблемы OPF строительство, e.грамм. .lp файл - полезен для отладки
формулировка ( строка ) - Формулировка линейных уравнений потока мощности для использования; должно быть один из [«углы», «циклы», «кирхгоф», «ptdf»]
ptdf_tolerance ( float ) - Значение, ниже которого записи PTDF игнорируются
free_memory ( устанавливает , по умолчанию {'pyomo'} ) - любое подмножество {‘pypsa’, ‘pyomo’}.Позволяет хранить временной ряд pypsa данные на время работы решателя (как расслоение на диск) и / или бесплатно pyomo данные после извлечения раствора.
extra_postprocessing (вызываемая функция ) - эта функция должна принимать три аргумента extra_postprocessing (сеть, снимки, двойники) и вызывается после модель решена, и результаты извлечены. Это позволяет пользователю извлеките дополнительную информацию о решении, например дополнительные теневые цены.
- Возвращает
- Тип возврата
Нет
- pypsa.opf.network_lopf_build_model (сеть , снимки = Нет , skip_pre = False , формулировка = 'углы' , ptdf_tolerance = 0,0 )
Построить модель pyomo для линейного оптимального потока мощности для группы снимков.
- Параметры
снимков ( список или индексный фрагмент ) - список снимков для оптимизации, должен быть подмножеством сеть.снимки, по умолчанию network.snapshots
skip_pre ( bool , по умолчанию False ) - пропустить предварительные шаги вычисления топологии, вычисления зависимые значения и поиск управления шиной.
формулировка ( строка ) - Формулировка линейных уравнений потока мощности для использования; должно быть один из [«углы», «циклы», «кирхгоф», «ptdf»]
ptdf_tolerance ( float ) - Значение, ниже которого записи PTDF игнорируются
- Возвращает
- Тип возврата
сеть.модель
- pypsa.opf.network_lopf_prepare_solver ( сеть , solver_name = 'glpk' , solver_io = Нет )
Подготовьте решающую программу для оптимального линейного потока мощности.
- Параметры
solver_name ( string ) - должно быть имя решателя, которое распознает pyomo, и это установлен, например «Глпк», «гуроби»
solver_io ( строка , по умолчанию Нет ) - параметр ввода-вывода решателя, e.грамм. «Питон» использовать «гуробипы» для solver_name = ”gurobi”
- Возвращает
- Тип возврата
Нет
- pypsa.opf.network_lopf_solve ( сеть , снимков = Нет , формулировка = 'углы' , solver_options = {} , solver_logfile = Нет , keep_files = Ложь , free_memory = {' } , extra_postprocessing = Нет )
Решите линейный оптимальный поток мощности для группы снимков и извлеките результаты.
- Параметры
снимков ( список или индексный фрагмент ) - список снимков для оптимизации, должен быть подмножеством network.snapshots, по умолчанию network.snapshots
формулировка ( строка ) - Формулировка линейных уравнений потока мощности для использования; должен быть одним из [«Углы», «циклы», «кирхгоф», «птдф»]; должен соответствовать формулировке, используемой для построение модели.
solver_options ( словарь ) - словарь с дополнительными параметрами, которые передаются решателю.(например, {‘thread’: 2} указывает gurobi использовать только 2 процессора)
solver_logfile ( None | string ) - Если не None, устанавливает параметр файла журнала решателя.
keep_files ( bool , по умолчанию False ) - сохранить файлы, которые pyomo создает из проблемы OPF строительство, например .lp файл - полезен для отладки
free_memory ( устанавливает , по умолчанию {'pyomo'} ) - любое подмножество {‘pypsa’, ‘pyomo’}.Позволяет хранить временной ряд pypsa данные на время работы решателя (как расслоение на диск) и / или бесплатно pyomo данные после извлечения раствора.
extra_postprocessing (вызываемая функция ) - эта функция должна принимать три аргумента extra_postprocessing (сеть, снимки, двойники) и вызывается после модель решена, и результаты извлечены. Это позволяет пользователю извлеките дополнительную информацию о решении, например дополнительные теневые цены.
- Возвращает
- Тип возврата
Нет
- pypsa.opf.network_opf (сеть , снимки = нет )
Оптимальный поток мощности для моментальных снимков.
Оптимальный поток мощности - обзор
9.3.4.1 Оптимальный поток мощности
В первой половине 20-го века система электроснабжения была «оптимизирована» инженерами с использованием комбинации суждений, опыта и практических правил, разработанных сетевые операторы.По мере того, как вычислительные технологии стали более распространенными и продвинутыми во второй половине 20-го века, инженеры начали использовать компьютеры для улучшения работы системы и, в частности, применять методы оптимизации для оптимизации потоков энергии в системе.
Оптимальный поток мощности (OPF) был впервые сформулирован в 1962 году Карпентье [15], а методы решения OPF были предложены в знаменательной статье Доммеля и Тинни в 1968 году [16]. С тех пор методы ОБТК стали критически важными для работы современных энергетических систем.Наиболее важное применение ОБТК - экономическая диспетчеризация. Это относится к проблеме планирования или «диспетчеризации» всех источников энергии, подключенных к системе, наиболее экономичным способом, или, другими словами, минимизации общих затрат на производство электроэнергии.
Эта оптимизация обычно ограничивается физическими ограничениями электрической сети, где все генераторы должны быть распределены таким образом, чтобы не нарушались потоки, напряжения и другие технические ограничения в линиях электропередач.Это сложная проблема, особенно в больших системах.
На рис. 9.7 показан пример тестовой сети IEEE со 118 узлами, которая часто используется для исследования и демонстрации OPF и методов экономической диспетчеризации. Это считается относительно небольшой системой; в реальных сетях может быть до 1000 или даже 10 000 узлов.
Рис. 9.7. Пример тестовой сети IEEE.
OPF также применяется для других аспектов работы системы, например, минимизация потерь энергии в сетях и минимизация воздействия на окружающую среду при эксплуатации системы (т.е., управление общей мощностью генераторов, выделяющих углерод в системе). Методы ОБТК также были приняты для целей планирования, включая максимальное увеличение количества ДГ и других распределенных энергетических ресурсов, которые могут быть подключены к распределительной сети [17,18].
OPF для минимизации общей стоимости генерации (проблема экономической диспетчеризации) формулируется следующим образом:
(9.9) minimFcost = ∑i = 1NgenfcostiPi
где fcosti - кривые затрат (кривые, описывающие соотношение между стоимостью генерации и выходной уровень) каждого системного генератора. P i - генерируемая мощность на генераторе i , а N gen - это полный набор генераторов в системе.
На ОБТК действуют ограничения электросети, некоторые из которых приведены ниже. Ограничения баланса потока мощности в уравнениях. (9.10) и (9.11) равны
(9.10) Pn = ∑n = 1N | Vn || Vm | Gnmcosθnm + Bnmsinθnm
(9.11) Qn = ∑n = 1N | Vn || Vm | Gnmsinθnm − Bnmcos
9000 где P n , Q n - вводимые фактическая и реактивная полезная мощность на шине n ; N - общее количество автобусов в системе; G нм , B нм - действительная и реактивная части элементов в матрице проводимости сетевой шины; и шина Y , соответствующая строке n -й и столбцу m -й (матрица проводимости шины или узловая матрица проводимости), шина Y описывает проводимость или обратное импедансу, Y = 1/ Z , между всеми узлами в системе, которые соединены линиями или трансформаторами.Угол θ нм - это разница углов напряжения между шинами n и m .
Кроме того, OPF должен удовлетворять ограничениям напряжения на шине в формуле. (9.12) и линейные тепловые ограничения в уравнении. (9.13).
(9,12) Vmin, n≤Vn≤Vmax, n
(9,13) | Sk | ≤ | Smax, k |
, где V min, n и V max, n - минимальное и максимальное допустимые напряжения на каждой сетевой шине n и S k - поток мощности в МВА через ветвь сети k. 2
Также возможно включить дополнительные ограничения в OPF, чтобы удовлетворить технические требования конкретной энергосети, например ограничения на определенные передачи мощности в части системы или настройки устройства РПН.
Пример 9.9Сформулируйте целевую функцию для минимизации потерь в ветвях электросети.
Целевая функция F потерь определяется как
minimFloss = ∑k = 1Nlinesflossk
Функция flossk для потерь в каждой ветви k в системе составляет
flossk = Pn − m + Pm− n
, где ветвь k соединяет узел n с узлом m .Интервальный оптимальный поток мощности, применяемый к распределительным сетям в условиях неопределенности нагрузок и возобновляемых ресурсов
Чтобы преобразовать (10) в эквивалентную детерминированную, мы сначала заменим интервальную арифметику на AA, а затем введем интервальное разложение Тейлора [25] для восстановления нелинейных ограничений с интервалами.
Введение AA и интервального расширения Тейлора
AA предоставляет хорошее решение для отслеживания корреляций между входными и вычисленными величинами, что позволяет гораздо более жестко ограничивать решения, чем IA, в вычислительном процессе.{+}] \) можно переписать как аффинное число, линейную комбинацию центрального значения и ряда шумовых членов:
$$ \ hat {x} = x_ {0} + x_ {1} \ varepsilon_ { 1} + x_ {2} \ varepsilon_ {2} + \ cdots + x_ {n} \ varepsilon_ {n} $$
(11)
где \ (x_ {0} \) - центральное значение; \ (\ varepsilon_ {i} \) представляет собой символ шума, значение которого неизвестно, но лежит в диапазоне [-1,1]; \ (x_ {i} \) - известный действительный коэффициент частичного отклонения.
Линейная операция \ (w = R (x, y) \) может быть преобразована в аффинную операцию \ (\ hat {w} = R (\ hat {x}, \ hat {y}) \), которая является составная процедура, вычисляющая аффинную форму \ (\ hat {w} \) для \ (w \), которая согласована с аффинными формами \ (\ hat {x} \) и \ (\ hat {y} \).В частности, операции сложения, вычитания и скалярного умножения задаются следующим образом:
$$ \ hat {x} \ pm \ hat {y} = (x_ {0} \ pm y_ {0}) + (x_ {1} \ pm y_ {1}) \ varepsilon_ {1} + \ cdots (x_ {n} \ pm y_ {n}) \ varepsilon_ {n} $$
(12)
$$ \ alpha \ hat {x} = (\ alpha x_ {0}) + (\ alpha x_ {1}) \ varepsilon_ {1} + (\ alpha x_ {2}) \ varepsilon_ {2} + \ cdots + (\ alpha x_ {n}) \ varepsilon_ {n} $$
(13)
где \ (\ alpha \) - постоянное число.
Существуют неаффинные операции, которые нельзя точно выразить как аффинную комбинацию символов шума. Хотя приближение Чебышева [26] и другие подобные подходы могут дать приблизительные результаты, процесс приближения с использованием составных неаффинных операций довольно сложен, и результат трудно выразить в интуитивно понятной форме. Для упрощения инженерной практики мы идем на компромисс, вводя интервальное разложение Тейлора первого порядка для построения аффинного приближения.{-})} 2}} \ правильно. \ kern-0pt} 2} \ ge 0 \) соответствуют частным отклонениям; \ (\ varepsilon_ {p, i} \) и \ (\ varepsilon_ {q, i} \) - символы шума активной и реактивной сетевой нагрузки на шине i th .
Поскольку (3) и (4) включают только аффинные операции, а именно линейную форму, которая может быть выражена точно как аффинная комбинация символов шума, после моделирования неопределенности для переменных состояния (3) и (4) могут быть выражены точно в аффинной форме:
$$ \ hat {p} _ {j} = \ hat {P} _ {ij} - r_ {ij} \ hat {\ ell} _ {ij} - \ sum \ limits_ { {k: (j, k) \ in {\ mathcal {E}}}} {\ hat {P} _ {jk}} $$
(16)
$$ \ hat {q} _ {j} = \ hat {Q} _ {ij} - x_ {ij} \ hat {\ ell} _ {ij} - \ sum \ limits _ {{k: (j, k ) \ in {\ mathcal {E}}}} {\ hat {Q} _ {jk}} $$
(17)
$$ \ hat {v} _ {j} = \ hat {v} _ {i} - 2 (r_ {ij} \ hat {P} _ {ij} + x_ {ij} \ hat {Q} _ { ij}) + (r_ {ij} ^ {2} + x_ {ij} ^ {2}) \ hat {\ ell} _ {ij} $$
(18)
где \ (\ hat {P} _ {ij} \ треугольник P_ {ij} ^ {\ text {c}} + P_ {ij} ^ {\ text {r}} \ varepsilon_ {P, ij} \) , \ (\ hat {Q} _ {ij} \ треугольник Q_ {ij} ^ {\ text {c}} + Q_ {ij} ^ {\ text {r}} \ varepsilon_ {Q, ij} \), \ (\ hat {\ ell} _ {ij} \ треугольник \ ell_ {ij} ^ {\ text {c}} + \ ell_ {ij} ^ {\ text {r}} \ varepsilon _ {\ ell, ij} \) и \ (\ hat {v} _ {i} \ треугольник v_ {i} ^ {\ text {c}} + v_ {i} ^ {\ text {r}} \ varepsilon_ {v, i} \) соответствуют аффинные формы \ (P_ {ij} \), \ (Q_ {ij} \), \ (\ ell_ {ij} \) и \ (v_ {i} \) соответственно.{\ text {r}} \ le \ bar {\ ell} _ {ij}} \\ \ end {array}} \ right. $$
(29)
При сравнении интервальных объективов обычно используются их средние точки и радиусы, где средние точки интервалов представляют их идентифицированные базовые местоположения, а их радиусы представляют их неопределенность. В (10) неопределенность целевой функции в основном зависит от неопределенностей требований нагрузки и выходных данных неуправляемых устройств, и эта информация является входными данными.{\ text {C}}, \ varvec {u}) \,} \ hfill \\ {{\ text {s.t. }} {(2), (15), (20) - (29)}} \ hfill \\ \ end {array}} \ right. $$
(30)
Следует отметить, что предложенная в этой статье модель I-OPF исследуется для сбалансированной распределительной сети, являющейся однофазной формулировкой. Неуравновешенность нагрузки - типичная характеристика распределительных сетей, особенно низковольтных распределительных сетей. Когда I-OPF требуется для несбалансированной системы, требуется трехфазная модель I-OPF, которую можно получить, используя трехфазную модель Distflow, полученную в [32] и [33], и применяя тот же процесс моделирования, что и описано в этой статье.
I-OPF зависит от особого характера радиальной распределительной сети, а именно от того, что ее потоки мощности могут быть определены с помощью простого набора линейных и квадратичных равенств, если углы напряжения исключены, а ограничения, построенные с центральными значениями, являются точными. Помимо полного удовлетворения ограничений в условиях неопределенности, интервальные расширения переменных состояния в модели также делают доступными рабочие границы решения, что является одним из преимуществ I-OPF или интервального программирования.
Эволюционные алгоритмы для определения оптимального потока мощности [OPF] (Конференция)
Албайджат, М. Х., и Шахидехпур, С. М. Эволюционные алгоритмы для определения оптимального потока мощности [OPF] . США: Н. П., 1999.
Интернет.
Албайджат, М. Х., и Шахидехпур, С. М. Эволюционные алгоритмы для определения оптимального потока мощности [OPF] .Соединенные Штаты.
Альбайджат, М. Х., и Шахидехпур, С. М. Мон.
«Эволюционные алгоритмы для решения оптимального потока мощности [OPF]». Соединенные Штаты.
@article {osti_697187,
title = {Эволюционные алгоритмы для определения оптимального потока мощности [OPF]},
author = {Албайджат, М. Х. и Шахидехпур, С. М.},
abstractNote = {По мере того, как электроэнергетика движется в более конкурентную среду, использование ОБТК будет становиться все более важным для максимального увеличения пропускной способности линий электропередачи.Задача OPF - это задача минимизации (максимизации) целевой функции с учетом ограничений-равенств, ограничений-неравенств. Обратите внимание, что целевая функция может принимать различные формы, такие как минимизация затрат на генерацию, минимизация электрических потерь в линии передачи, минимальная смена генерации, минимизация графика сброса нагрузки в аварийных условиях или другие управляющие переменные. Суть OPF в том, что целевая функция должна удовлетворять всем ограничениям.OPF - это задача оптимизации, для решения оптимального потока мощности предлагается множество методов оптимизации. Часть этих методов основана на методе исчисления, часть - на методе случайного поиска, а часть - на эвристических методах. Предлагаемый авторами метод представляет собой метод эвристического поиска, основанный на концепции Evolution, при котором наиболее подходящее решение сохранится для следующего поколения или следующей итерации. Основное преимущество таких методов оптимизации состоит в том, что авторы используют параметры функции приспособленности, но не производную функции.},
doi = {},
url = {https://www.osti.gov/biblio/697187},
journal = {},
number =,
объем =,
place = {United States},
год = {1999},
месяц = {11}
}
Оптимальные методы перетока мощности при характеристике традиционных и возобновляемых источников энергии: всесторонний анализ
Исчерпывающие знания методов оптимального потока мощности (OPF) имеют решающее значение для правильной работы и планирования системы, поскольку методы OPF используются для поиска оптимального состояния любая система в условиях ограничений системы, таких как минимизация потерь, ограничения реактивной мощности, тепловые ограничения линий передачи и оптимизация реактивной мощности.Использование возобновляемых источников энергии позволило оптимизировать поток энергии в системе при различных ограничениях. Эта работа представляет собой всестороннее исследование методов оптимальных потоков энергии с ограничениями традиционных и возобновляемых источников энергии. Кроме того, эта работа представляет прогресс решения оптимального потока мощности от его начала до его нынешней формы. Авторы классифицируют методы оптимального перетока мощности при различных условиях ограничений традиционных и возобновляемых источников энергии. Представлены текущие и будущие применения программ оптимального потока мощности в интеллектуальном системном планировании, эксплуатации, расчете чувствительности и управлении.Это исследование поможет инженерам и исследователям оптимизировать поток энергии с использованием традиционных и возобновляемых источников энергии.
1. Введение
ОБТК в энергосистеме представляет собой задачу оптимизации при различных ограничениях. Это практически значимое и хорошо изученное подполе ограниченной оптимизации. Важной особенностью ОБТК является наличие уравнений потока нагрузки в системе ограничений-равенств. Карпентье [1] представил проблему OPF в 1979 году. Карпентье представил OPF как расширение проблемы оптимального экономического диспетчеризации (ED) генерации в традиционных энергосистемах.Ключевым вкладом Карпентье было включение уравнений потока электроэнергии в формулировку ED. Методы OPF являются традиционными и основаны на метаэвристике. На рисунке 1 показана классификация традиционных и метаэвристических методов.
Кроме того, из-за большой интеграции возобновляемых источников энергии в традиционную энергосистему очень важно учитывать неопределенности в расчетах ОБТК.
OPF во многом зависит от метода статической оптимизации для минимизации скалярной функции оптимизации.Доммел и Тинни [2] представили OPF в 1968 году с целью минимизации, в котором алгоритм градиента первого порядка подчиняется ограничениям равенства и неравенства. Momoh et al. [3] использовали ОБТК для решения проблем дерегулируемой электротехнической промышленности. Далее авторы использовали ОБТК для решения проблем вертикального рынка электроэнергии.
В этой статье авторы представляют всестороннее исследование методов оптимального потока мощности. В разделе 2 представлен обзор методов ОБТК с традиционными источниками энергии.В разделе 3 авторы рассмотрели методы ОБТК с возобновляемыми источниками энергии. В разделе 4 представлен сравнительный анализ различных методов ОБТК с последующим заключением.
2. ОБТК для энергосистемы с традиционными источниками энергии
Существуют различные методы решения проблемы оптимального потока мощности с традиционными источниками энергии. Некоторые из них следующие.
2.1. Математические методы
Классические математические методы (градиентное, ньютоновское, линейное, целочисленное программирование и др.)) позволяют находить оптимальные решения реальных проблем.
2.1.1. Градиентный метод
В январе 2004 г. Sun et al. В [4] предложена схема на основе штрафов для OPF с переходной стабильностью, в которой метод сопряженных уравнений вычисляет градиент штрафного члена, связанного с ограничениями устойчивости. Такой подход с использованием сопряженных уравнений значительно снижает вычислительные затраты.
2.1.2. Метод Ньютона
В 1984 г. Дэвид и др. В [5] представлен метод решения классической задачи ОБТК с несепарабельной целевой функцией.Классический OPF - это задача с управляемыми переменными, которая регулируется для оптимизации целевой функции путем удовлетворения физических и рабочих ограничений. В 2007 году Пизано-Мартинес и др. В [6] представлена основанная на алгоритме Ньютона модель системы преобразователя источника напряжения постоянного тока высокого напряжения (VSC-HVDC), которая подходит для решений OPF. Способность VSC-HVDC обеспечивать независимое управление величинами переменного напряжения преобразователя и фазовыми углами хорошо представлена моделью, которая позволяет управлять активной и реактивной мощностью отдельно для регулирования системы.В 2012 году Zhao et al. [7] предложили вариант алгоритма ( PDIPM) метода первично-двойных внутренних точек, основанный на непрерывном методе Ньютона, для повышения устойчивости PDIPM. Алгоритм Ньютона в PDIPM заменен непрерывным методом Ньютона. Разработанный метод свидетельствует о хорошей устойчивости и исключительной способности к схождению. В 2000 году Амбриз-Перес и др. [8] представили усовершенствованные модели потока нагрузки для статического компенсатора VAR (SVC). Модели объединяются в текущий поток нагрузки (LF) и алгоритм Ньютона OPF.Полные модели восприимчивости и угла открытия SVC подходят для обычного и оптимального анализа потока мощности. В 2009 году Милано [9] представил непрерывную версию метода Ньютона для решения проблемы потока мощности. Он имеет два основных вклада: во-первых, это общая структура для применения эффективных методов численного интегрирования для решения плохо обусловленных или плохо инициализированных случаев потока мощности, а во-вторых, формальная классификация существующих числовых схем для решения проблемы потока мощности.
2.1.3. Линейное, нелинейное и полуопределенное программирование
В 1998 году Wei et al. [10] представил новый алгоритм нелинейного программирования внутренней точки для OPF, который основан на непростых условиях Куруша-Куна-Таккера (KKT) исходной задачи, но не на методе логарифмических барьерных функций. Благодаря концепции центрирующего направления метод внутренней точки распространяется на классические задачи потока мощности (C-PF) и приближенные OPF (A-OPF). В 2008 году Bai et al. [11] представили новое решение, использующее метод полуопределенного программирования (SDP) для решения OPF.Разработанный метод включает переформулирование задач ОБТК в модель SDP и разработку алгоритма метода внутренней точки (IPM) для SDP. На основе SDP проблема OPF решается с помощью алгоритмов прямой-двойственной внутренней точки, которые обладают суперлинейной сходимостью. В 1994 году Гранвиль [12] представил применение метода внутренней точки, основанного на первично-дуальном алгоритме, к оптимальному распределению реактивной мощности (ORPD), которая представляет собой крупномасштабную задачу невыпуклого нелинейного программирования с нелинейными ограничениями.В 2005 году Zhang et al. [13] представили нелинейный метод оптимального потока мощности (OPF) во внутренней точке, основанный на формулировке текущего несоответствия в прямоугольных координатах.
2.1.4. Математические методы без категорий
В 2015 году Abdelouadoud et al. [14] представили алгоритм релаксации конуса второго порядка (SOC) для решения OPF на основе модели ветвления потока радиальной и сбалансированной системы распределения. В 2016 году Баран и Фернандес [15] представили трехфазный OPF, который включает взаимные импедансы, чтобы минимизировать потери системы.В 2016 году Гарсес [16] представил квадратичное приближение для OPF в системах распределения электроэнергии. Предлагаемый метод основан на линеаризованном потоке нагрузки, который эффективен как для систем распределения электроэнергии, так и для трехфазной несимметричной работы. В 2015 году Эмили Маноранджитам и Шунмугалата [17] представили процесс решения ОБТК в энергосистеме, в котором использовался UPFC. Этот UPFC восстанавливает способность передачи мощности и переходную стабильность, а также снижает потери при передаче и затраты на топливо для генерации.В 2016 году Xu et al. [18] представили превентивно-корректирующий оптимальный поток мощности с ограничениями безопасности (PCSCOPF) для достижения наилучшей координации между превентивным управлением (PC) и корректирующим управлением (CC) с учетом вероятностного характера непредвиденных обстоятельств и стоимости CC, а также другие ограничения привязки. В 2015 году Zhang et al. [19] представили оптимальную модель комбинированного потока углеродной энергии (OCECF), которая решается с помощью обучения с помощью нового оценочного многокритериального решения (AIMS) ( λ ).Выбросы углерода, стоимость топлива, потери активной мощности, отклонение напряжения и потери выбросов углерода выбираются в качестве целей оптимизации. В 2015 году Zhao et al. [20] предложили модель динамического оптимального потока реактивной мощности с ограничениями по стабильности напряжения (VSC-DORPF). Это снижает ежедневные потери в сети, улучшает качество напряжения и повышает стабильность напряжения в энергосистеме. В 2016 году Ван и др. [21] представили математический метод решения корректирующей модели оптимального потока мощности с ограничениями безопасности (CRB-SCOPF), основанной на рисках, которая учитывает корректирующие возможности системы после возникновения непредвиденных обстоятельств.Предлагаемый метод применяет лагранжевую релаксацию к ограничениям риска системы, а затем применяет декомпозицию изгибающих устройств к оставшейся лагранжевой подзадаче.
2.2. Метаэвристические алгоритмы
Метаэвристические методы - это мощные и гибкие поисковые методологии, успешно решающие практически сложные проблемы. Эвристические и метаэвристические алгоритмы стремятся производить решения хорошего качества за разумное время вычислений, которые достаточно хороши для практических целей.
2.2.1. Генетический алгоритм
В 2002 году Бакирцис и др. [22] представили OPF, который представляет собой нелинейную, невыпуклую, крупномасштабную задачу статической оптимизации, основанную на усовершенствованном генетическом алгоритме (EGA). Для решения OPF используются как непрерывные, так и дискретные управляющие переменные. В 1995 году Ли и др. [23] представили усовершенствованный простой генетический алгоритм, используемый для планирования системы реактивной мощности. Кроме того, предлагается новый метод отбора и генерации популяции, в котором используется метод отсечения Бендера.В 1998 году Ли [24] представил сравнительное исследование трех эволюционных алгоритмов (EAs) для решения задачи оптимального планирования реактивной мощности (ORPP). Задача ORPP разбита на модули оптимизации, а эволюционные алгоритмы оптимизируют каждый модуль итеративным образом для получения глобального решения. В 2006 году Тодоровски и Райичич [25] представили новый метод решения проблемы OPF с использованием генетического алгоритма. Это зависит от применения новой процедуры инициализации, которая использует углы напряжения на шинах генератора в качестве управляющих переменных для достижения напряжений на шинах нагрузки с меньшими вычислениями.
2.2.2. Оптимизация роя частиц
В 2002 году Абидо [26] представил алгоритм оптимизации роя частиц (PSO), основанный на эффективном и надежном подходе к решению проблемы ОБТК. Предлагаемый подход использует глобальные и локальные исследовательские возможности PSO для изучения оптимальной настройки управляющих переменных. Были рассмотрены различные целевые функции для минимизации затрат на топливо, улучшения профиля напряжения и повышения стабильности напряжения. В 2006 году Влахогианнис и Ли [27] представили три типа алгоритмов PSO: расширенное общее пассивное собрание (GPAC), локальное пассивное собрание (LPAC) с подходом фактора ограничения, основанным на операторе пассивного собрания, и CA, основанным на координированном агрегировании. оператор.Предложенные алгоритмы PSO и алгоритм на основе консервативной внутренней точки OPF конкурировали в задачах оптимизации управления реактивной мощностью и напряжением. В 2005 году Эсмин и др. [28] представили подход к оптимизации потерь мощности с помощью алгоритма PSO и улучшили PSO до гибридного алгоритма PSO (HPSO). Предлагаемый подход использует локальные и глобальные возможности для поиска решения оптимального снижения потерь за счет установки шунтирующего компенсатора реактивной мощности. В 2008 году Чжан и Лю [29] представили формулировку многокритериальной задачи управления реактивной мощностью и напряжением.Многокритериальная проблема решена с помощью стратегии нечеткой оптимизации и нечеткой адаптивной оптимизации роя частиц (FAPSO). Факторами являются потеря активной мощности, отклонение напряжения и индекс стабильности напряжения системы. В 2009 году Аль-Рашиди и Эль-Хавари [30] представили полную формулировку оптимизации роя разнородных частиц (PSO), которая применяется для решения задач оптимизации в энергосистемах. В 2016 году Су и др. [31] представили основанную на оптимизации последовательную стратегию и стратегию в реальном времени на основе многокритериальной оптимизации для оптимального размещения и управления переключаемыми конденсаторами, соединенными треугольником.Принимая во внимание колебания нагрузки, сформулирована полная оптимизация размещения конденсаторов, чтобы увеличить чистую годовую прибыль от сокращения потерь в сети и высвобождения емкости. Далее представлена последовательная стратегия, основанная на анализе чувствительности к потерям, для эффективного размещения конденсаторов в крупномасштабных несимметричных распределительных сетях. В 2008 году Valle et al. [32] представили исчерпывающий обзор основных концепций PSO и его вариантов. Кроме того, представлено комплексное исследование различных проблем энергосистемы, которое решает PSO.В 2016 году Singh et al. [33] использовали устаревающего лидера и претендентов PSO (ALC-PSO) для решения различных типов проблем ОБТК энергосистемы с несколькими типами сложности и мощности.
2.2.3. Без рубрики Метаэвристические и поисковые алгоритмы
В 2011 году Niknam et al. [34] представили улучшенный алгоритм перемещения лягушки (SLFA) для решения проблемы выбросов ОБТК в энергосистемах с учетом как экономических, так и экологических проблем. Предлагаемый метод дает оптимальные значения с учетом различных целей, включая лучшую стоимость и лучшую эмиссию.В 2014 году Ghasemi et al. [35] представили алгоритмы хаотической инвазивной оптимизации сорняков (CIWO), основанные на хаосе, и исследовали их эффективность для оптимальных настроек OPF и его управляющих переменных. В 2016 году Abaci и Yamacli [36] представили метод оптимизации на основе дифференциального поиска для решения различных типов задач, включая сложные, одноцелевые и многокритериальные функции в рамках ограничений, касающихся оптимального потока мощности (OPF). В 2016 году Ачарджи [37] представил самоадаптивный дифференциальный эволюционный алгоритм (SADE) для увеличения и управления потоком мощности с использованием унифицированного контроллера потока мощности (UPFC) в условиях практических ограничений безопасности (SC).В 2016 году Ардешири Ладжими и Амраи [38] представили формулировку оптимального потока мощности (TSCOPF), основанную на искусственной нейронной сети (ИНС), с ограничением устойчивости при переходных процессах с использованием империалистического конкурентного алгоритма (ICA). Чтобы увеличить переходную устойчивость энергосистемы по углу ротора к большим возмущениям, критическое время отключения используется в качестве показателя переходной устойчивости. В 2016 году Аян и Килич [39] представили решение проблемы ОБТК для силовых систем постоянного тока высокого напряжения (HVDC) с помощью алгоритма поиска с возвратом (BSA).Чтобы продемонстрировать применимость и эффективность BSA, используются три разные тестовые системы. В 2016 году Дариани и др. [40] представили алгоритм адаптивной групповой поисковой оптимизации (AGSO) для решения задачи оптимального потока мощности (OPF). В 2015 году Махдад и Срайри [41] представили новый подход к планированию энергосистемы, который основан на гибридном алгоритме светлячков (FFA) и алгоритме поиска паттернов (PS) и поддерживается правилами мозгового штурма для минимизации общих затрат на топливо, потерь мощности и напряжения. отклонение.В 2015 году Мукерджи [42] представил алгоритм хаотического крилевого стада (CKHA) для решения проблемы OPF энергосистемы с различными целевыми функциями и повышения производительности базового метода KHA. В 2016 году Мукерджи и Мукерджи [43] представили новый алгоритм стада криля на основе оппозиции (OKHA), метаэвристический алгоритм, для решения проблемы OPF энергосистемы, объединенной с устройствами гибких систем передачи переменного тока (FACTS). В 2016 году Пандиараджан и Бабулал [44] представили алгоритм поиска гармонии на основе нечеткой логики (FHSA) для решения проблемы оптимального потока мощности для повышения безопасности в энергосистеме.Рассмотрены задачи минимизации стоимости топлива и индекса серьезности. Стоимость топлива сводится к минимуму за счет изменения активной мощности генератора, величины напряжения на шине генератора, отводов трансформатора и VAR шунтов. В 2016 году Прасад и Мукерджи [45] представили метаэвристический алгоритм поиска симбиотических организмов (SOS) для решения проблемы OPF для энергосистемы, оснащенной устройствами FACTS. В 2015 году Рамеш Кумар и Премалата [46] представили метод адаптивной оптимизации на основе реальной кодированной биогеографии (ARCBBO) для решения различных целевых функций задач ОБТК с несколькими физическими и эксплуатационными ограничениями.К различным целям относятся минимизация затрат на топливо, минимизация потерь активной мощности, минимизация выбросов, профиль напряжения и повышение стабильности напряжения. В 2015 году Венкатешвара Рао и Нагеш Кумар [47] использовали алгоритм BAT для минимизации потерь реальной мощности в энергосистеме. Дальнейшая задача оптимального потока мощности решается с помощью унифицированного регулятора потока мощности. В 2015 году Юань и др. [48] представили модернизированный алгоритм создания искусственных пчелиных семей с квантовой теорией и оператором хаотического локального поиска (QCABC) для решения проблемы OPF.
3. ОБТК энергосистемы с возобновляемыми источниками энергии
3.1. Распределенная генерация (DG)
В 2011 году Аманифар и Хамедани Гольшан [49] представили алгоритм PSO для поиска оптимального расположения и размеров DG с целью минимизировать общую стоимость системы, реальные потери мощности и количество устанавливаемых ДГ. В 2005 году Харрисо и Уоллес [107] представили поставленные правительством цели и стимулы для увеличения мощности подключения распределенной генерации к распределительным сетям.В 2012 году Пажери и др. [50] представили формулировку проблемы диспетчеризации экономики / окружающей среды (EED) для гибридной системы, которая включает тепловые генерирующие установки, солнечные, ветровые и возобновляемые накопители. Анализ проводится с использованием моделирования MATLAB для области солнечного излучения с высокой степенью облучения. В 2014 году Ник и др. [51] представили оптимальное размещение распределенных систем хранения (DSS) в активных распределительных сетях (ADN), описав многокритериальную задачу оптимизации для поиска оптимального компромисса между техническими и экономическими целями.В 2010 году Атва и др. [52] предложили метод вероятностного планирования для оптимального распределения различных типов ДГ (т. Е. ДГ ветра, ДГ солнца и ДГ биомассы) в системе распределения, чтобы минимизировать ежегодные потери энергии. В 2013 году Георгилакис и Хациаргириу [108] представили исчерпывающее описание различных моделей и методов оптимизации для решения проблемы оптимального размещения ГД (ODGPP) для изучения, а также классификации текущих и будущих исследовательских подходов в этой области. В 2014 году Gill et al.[53] представили широкую структуру динамического оптимального потока мощности (DOPF) для схем активного управления сетью (ANM). Технологии ANM ориентированы на интертемпоральные эффекты. DOPF смоделирован для сокращения использования возобновляемых источников энергии, хранения энергии и гибкого спроса. В 2015 году Джабр и др. [54] представили разреженную формулировку аффинно настраиваемого робастного аналога (AARC) многопериодной проблемы OPF с ВИЭ и хранением. В 2012 году Моради и Абдини [55] представили комбинированный метод решения проблем размещения и пропускной способности для DG.В этом методе используются GA и PSO для определения местоположения и мощности DG соответственно. В 2011 году Сортомм и Эль-Шаркави [109] представили потенциальную прибыль и эффекты однонаправленного транспортного средства на опоясание (V2G). В 2007 году Ян и др. [56] представили модель оптимизации размеров гибридной системы солнечного ветра (HSWSO) для оптимизации размеров мощности гибридных систем выработки энергии солнечным ветром, использующих аккумуляторную батарею. В 2011 году Атва и Эль-Саадани [57] представили метод вероятностного планирования для оптимального выполнения ветровой распределенной генерации (ДГ) в распределительных системах, чтобы минимизировать ежегодные потери энергии.В 2007 году Ашок [110] обсудил различные системные устройства для гибридной энергетической системы с целью улучшения универсальной модели и нашел оптимальную комбинацию компонентов энергии для снабжения сельского сообщества. В 2016 году Bouhouras et al. [111] представили оптимизацию, касающуюся размещения и определения размеров блоков DG в распределительных сетях (DN) для минимизации потерь. В 2015 году Азизипана-Абаргуи и др. В [112] представлена вероятностная задача ОБТК для системы, состоящей из тепловых блоков (ТУ), ветряных электростанций (ВЭС), фотоэлектрических элементов (ФЭ) и комбинированного производства тепла и электроэнергии (ТЭЦ).В 2016 году Wei et al. [58] предложили метод интегрирования DG, основанный на стохастическом оптимальном потоке мощности (S-OPF). Моделируется недорогая оптимальная модель интеграции DG для операторов распределительных систем (DSO). В 2013 году Лин и Чен [59] представили алгоритм распределенного и параллельного OPF (DPOPF). Кроме того, предлагается механизм вычислительной синхронизации на основе сети Петри (PN) для решения проблемы системы передачи интеллектуальной сети OPF (OPFSG). В 2015 году Summers et al. В [60] представлена стохастическая многопериодная задача OPF, для которой семейство выпуклых грубых вычислений используется для компромисса между стоимостью и безопасностью различными способами.В 2016 году Тазвинга и др. [113] представили оптимальную модель гибридной системы управления энергией на основе фотоэлектрических-дизельных аккумуляторных батарей (PDB) для снижения затрат на топливо и износа аккумуляторных батарей. Он также определяет оптимальный поток мощности, доступность фотоэлектрической энергии, состояние заряда аккумуляторной батареи и потребляемую мощность нагрузки. В 2016 году Чен и др. [61] представили основанный на PSO метод оптимального управления мощностью для учета неопределенных условий вождения гибридных электромобилей (HEV). В 2015 году Ма и др. [114] представили технико-экономический анализ автономной гибридной системы хранения с солнечно-ветровой накачкой для изолированной микросети.В 2017 году Sichilalu et al. В [62] представлена модель оптимального управления (OC) водонагревателя с тепловым насосом (HPWH), который питается от системы ветрогенератор-фотоэлектрическая сеть. Целевая функция - минимизация затрат на электроэнергию, которая учитывает тариф на электроэнергию по времени использования.
3.2. Microgrid
В 2011 г. Sanseverino et al. [63] представили подход к мониторингу исполнения и перепланированию для решения проблемы оптимальной диспетчеризации генерации в интеллектуальной сети за счет минимизации выбросов углерода и производственных затрат, а также повышения качества.В 2015 году Shi et al. [64] представили онлайн-стратегию управления энергопотреблением (EMS) для работы микросетей в реальном времени. В 2013 году Dall’Anese et al. [65] представили численные тесты. Основная роль предлагаемого подхода заключается в достижении глобально оптимального решения исходного невыпуклого оптимального потока мощности. В 2012 году Battistelli et al. [115] представили инструмент оптимизации для управления энергопотреблением в малых энергетических системах, объединенных с системами V2G. В 2011 году Chen et al. [66] представили интеллектуальную систему управления энергопотреблением (SEMS) для оптимальной организации производства электроэнергии из источников РГ и системы накопления энергии (ESS), а также для минимизации эксплуатационных расходов микросетей.В 2012 году Лян и др. [67] представили алгоритм управления динамическим стохастическим оптимальным потоком мощности (DSOPF), основанный на широкомасштабных измерениях, с использованием метода адаптивного критического дизайна (ACD). В 2013 году Леврон и др. [68] представили оптимальную систему управления энергопотреблением запоминающих устройств в сетевых микросетях. Накопленная энергия контролируется для балансировки нагрузок и возобновляемых источников, а также для минимизации общей стоимости энергии в точке общего соединения (PCC). В 2011 году Могхаддам и др. [69] представили алгоритм оптимизации с многоцелевым адаптивным модифицированным PSO (AMPSO) для решения проблемы многооперационного управления в типичном MG с возобновляемыми источниками энергии (RES).В 2010 году Morais et al. [70] представили операционную оптимизацию изолированной системы с помощью виртуального производителя электроэнергии (VPP). Основная цель - выбрать лучшую стратегию управления VPP, чтобы минимизировать затраты на генерацию и оптимизировать время зарядки и разрядки хранилища с учетом всех эксплуатационных ограничений. В 2011 году Танака и др. [116] представили подход к оптимальной работе интеллектуальной сети, чтобы минимизировать колебания потока мощности в точках соединения. Для достижения запланированной оптимальной работы используются распределенные регулируемые нагрузки, такие как аккумулятор и тепловой насос.В 2015 году Alavi et al. В [71] предложен оптимальный подход для работы MG в изолированном режиме. Неопределенности, связанные с выпуском возобновляемых ресурсов и спросом, демонстрируются методом точечной оценки (PEM) и устойчивой оптимизацией (RO), соответственно. В 2014 году Бахмани-Фирузи и Азизипана-Абаргуи [72] представили эффективный план исследований по управлению операциями MG в отношении эксплуатации, технического обслуживания и финансовых вопросов. При оптимизации исследований MG учитывалась фиксированная стоимость и стоимость обслуживания аккумуляторного накопителя энергии (BES).Надежный и эффективный метаэвристический подход с улучшенным алгоритмом летучей мыши (IBA) используется для разработки корректирующих стратегий и выполнения диспетчеризации с наименьшими затратами. В 2015 году Bracale et al. [117] представил оптимальный подход к управлению микросетью постоянного тока (DCMG), который включал в себя управляемые (например, микротурбины) и неуправляемые (например, фотоэлектрические генераторы) блоки генерации, систему хранения и управляемые / неуправляемые нагрузки. Этот подход разработан для минимизации ежедневных общих затрат на электроэнергию. В 2015 году Голами и др.[73] использовал GA с новыми настройками и операторами, который позволяет размещать конденсаторы как в изолированном, так и в подключенном к сети режимах при различных уровнях нагрузки. В 2012 году Хоррамдел и Рауфат [74] представили подход стохастического программирования для планирования реактивной мощности MG в условиях неопределенности ветряных электростанций. Многоцелевая функция с целями минимизации потерь, резерва реактивной мощности и максимизации запаса прочности по напряжению оптимизирована с помощью четырехэтапного многоцелевого нелинейного программирования.В 2016 году Lv et al. [75] предложили многоцелевой двухуровневый алгоритм оптимизации. Модель верхнего уровня определяет оптимальную диспетчеризацию распределительной сети (DN) для достижения минимальных потерь мощности и профиля напряжения. Модель нижнего уровня рассматривает эксплуатационные расходы микросетей (MG) как цель для определения оптимальной схемы работы распределенных генераторов DG. В 2015 году Макларти и др. [118] представили два оптимизационных подхода к отгрузке холодильной установки с несколькими чиллерами с теплоаккумулятором холодной воды.Целью оптимизации является снижение затрат и выбросов с учетом реальных эксплуатационных ограничений завода. В 2015 году Рива Сансеверино и др. [119] представили новый алгоритм OPF для изолированного MG. Алгоритм обеспечивает минимальные потери и стабильную рабочую точку с соответствующими параметрами спада, которые используются для регулирования первичного напряжения и частоты. В 2015 году Sharma et al. [76] представили оптимизацию на основе квазиоппозиционной модели гриппа свиней с карантином (SIMBO-Q) для снижения общих эксплуатационных расходов MG с учетом оптимального размера аккумуляторной батареи.
3.2.1. Микросеть с возобновляемыми источниками энергии и / или аккумуляторной системой хранения энергии
В настоящее время аккумуляторная система хранения является жизненно важным компонентом в технологии микросетей. Для оптимизации инвестиций в емкость хранилища центра обработки данных Томпсон и др. [120] представили метод. В [77] Sharma et al. использовали метод оптимизации серого волка для поиска оптимальной емкости накопителя энергии. В [121] Кришнамурти и Квасински обсуждали отказоустойчивость электросетей в сложных условиях.Xu et al. [122] представили инженерный опыт с системой хранения энергии. Для оптимизации емкости памяти в микросетях Liu et al. [78] предложили оптимальную схему согласованного планирования. В [123] Ходабахш и Сируспур разработали две разные методологии для оперативного управления системой хранения с изменяющимся горизонтом. Шен и др. [79] представили схему управления энергией для микросети, которая содержит аккумуляторные батареи, дизельные генераторы, фотоэлектрические панели и ветер. Для оптимальной работы стоянки для электромобилей Guo et al.[80] представили двухуровневую структуру. Для управления частотой микросети Hassanzadehfard et al. [124] использовали аккумуляторные батареи в качестве долговременных хранилищ, а ультраконденсаторы в качестве краткосрочных хранилищ. Для расчета оптимальной номинальной мощности и емкости накопителя энергии Альхарби и Бхаттачарья [125] разработали модель оптимизации.
3.2.2. Технология электромобилей
Последние разработки в области технологии электромобилей имеют большое влияние на работу микросетей. Для возобновляемых источников энергии и интеграции транспортных средств в сетевые системы, Melhem et al.[81] предложили систему управления энергией в жилых домах. Yu et al. [82] исследовали модель, чтобы найти влияние технологии электромобилей на мобильность в ответ на спрос. Для интеграции электромобиля в умную сеть Laureri et al. [126] разработали методику оптимизации. Патеракис и др. [83] представили модель оптимизации для минимизации затрат на закупку энергии в умном доме. Ли и др. [84] представили онлайн-методологию составления расписания с учетом затрат. Для зарядки электромобиля Yao et al.[127] представили схему зарядки в реальном времени.
3.3. Solar
В 2012 году Lin et al. [85] использовали стратегию ограничения активной мощности, чтобы уменьшить инжекцию фотоэлектрической мощности во время пикового солнечного излучения, чтобы избежать нарушения напряжения. В 2015 году Мартин [86] представил процесс концентрированной солнечной электростанции, основанный на регенеративном цикле Ренкина. Кроме того, технологии сухого охлаждения оптимизированы с помощью методов математического программирования. В 2014 году Bianchi et al. [128] представили гибридную фотоэлектрическую / аккумуляторную систему, чтобы поддержать оптимальную конструкцию гибридной системы с точки зрения количества фотоэлектрических модулей, наклона фотоэлектрических модулей, а также количества и емкости батарей.В 2015 году Burlafinger et al. [87] использовали селективные поглотители для электростанций концентрированной солнечной энергии (CSP), чтобы минимизировать тепловые потери и повысить эффективность. Кроме того, потенциал солнечного поглотителя тепла оптимизирован за счет использования селективных абсорбционных свойств и температуры. В 2016 году Guo et al. [88] представили оптимальное отношение падения давления в турбине к доступному общему перепаду давления и широко исследовали его с помощью теоретического анализа и трехмерного численного моделирования для солнечной дымоходной электростанции (SCPP).В 2015 году Ха и Вакилоройя [129] рассмотрели проблему моделирования и управления полностью разработанным гибридным сплит-системой с солнечной системой кондиционирования воздуха, чтобы улучшить производительность существующей солнечной системы кондиционирования воздуха. В 2013 году Lizarraga-Garcia et al. [130] представили пример оптимизации для переменной времени работы приемника солнечной энергии по запросу (CSPonD) и накопителя тепловой энергии. В исследовании рассматриваются такие факторы, как изменяющиеся во времени цены на электроэнергию и обратный выкуп электроэнергии из сети.В 2017 году Mokheimer et al. [131] представили интегрированную солнечную газотурбинную когенерационную установку (ISGCP), которая вырабатывает электричество и производит технологический пар с постоянной скоростью 81,44 кг / с при 45,88 бар и 394 ° C в течение года. В дополнение к этому, производство электроэнергии исследуется для различных газотурбинных генерирующих мощностей. В 2014 году Назир и др. [89] представили оптимизацию потока мощности фотоэлектрической системы, подключенной к сети. Оптимизация была выполнена путем вычисления корня уравнения активной мощности (ma, α ) и уравнения реактивной мощности (ma, α ) с использованием метода Ньютона-Рафсона.В 2016 году Нцалуба и др. [90] представили оптимизацию расхода солнечной системы водяного отопления (SWHS) с особым упором на оптимизацию расхода насоса. В 2015 году Ван и др. [91] представили подход к анализу оптимальной мощности и экономической целесообразности гибридной системы хранения энергии (HESS), поддерживающей отправку фотоэлектрической (PV) электростанции мощностью 30 МВт.
3.4. Wind
В 2014 г. Rabiee et al. В [92] представлена полная формулировка ОБТК для энергосистемы с неопределенной подачей ветровой энергии через линии высоковольтного постоянного тока (LCC-HVDC) преобразователя с коммутацией линий, преобразователь источника напряжения (VSC-HVDC) и индукционные генераторы с двойным питанием (DFIG). ).Цель состоит в том, чтобы максимизировать устойчивость общих затрат к прерывистой выработке ветровой энергии, используя теорию принятия решений по информационным промежуткам (IGDT). В 2016 году Ke et al. [93] представили новую модель вероятностного оптимального потока энергии (POPF) со случайными ограничениями, которая отражает неопределенности ветровой генерации (WPG) и нагрузок. В 2014 году Bienstock et al. [94] представили метод, который зависит от случайных ограничений, чтобы ограничить вероятность того, что любая линия (или генератор) будет перегружен, вместе с оптимальным онлайн-контролем, который учитывает управляемую реакцию генератора на колебания возобновляемой энергии.В 2011 году Brekken et al. [132] представили процедуры определения размеров и контроля для системы хранения энергии на основе проточной цинк-бромной батареи. Результаты показывают, что благодаря эффективному контролю и координации систем накопления энергии ожидаемая мощность ветряных электростанций увеличивается, а стоимость комбинации, связанная с необходимыми запасами, снижается. В 2013 году Гофрани и др. [95] представили оптимальное размещение накопителей энергии в нерегулируемой энергосистеме для минимизации почасовых социальных затрат.С помощью исторических данных и подбора кривой как ветер, так и нагрузка моделируются стохастически. Рыночный вероятностный оптимальный поток энергии (POPF), усовершенствованный GA, с интеграцией накопителей энергии и ветроэнергетики, максимизирует использование энергии ветра в течение периода планирования. В 2009 году Джабр и Пал [96] представили стохастическую модель ветроэнергетики в диспетчерской программе ОБТК. Модель связана с координацией ветровой и тепловой энергии с учетом ожидаемых штрафных затрат за неиспользование всей доступной энергии ветра и ожидаемых затрат на использование резервов мощности из-за нехватки энергии ветра.В 2016 году Sedghi et al. [133] представили методику планирования для определения оптимального местоположения, емкости и номинальной мощности батарей при минимизации функции затрат при технических ограничениях. Целевая функция включает денежные факторы, такие как затраты на инвестиции, эксплуатацию и надежность, а также фактор технических штрафов. В 2014 году Себастьян и др. [97] представили вероятностный оптимальный поток мощности переменного тока (POPF), который учитывает изменение нагрузки, стохастическое поведение ветра и переменную тепловую мощность линии, которая обычно используется в качестве детерминированного значения в нескольких исследованиях.В 2015 году Aien et al. [98] рассмотрели вероятностные методы, используемые для вероятностного оптимального потока мощности (POPF), и предложили метод с использованием техники нецентрированного преобразования (UT). В 2013 году Arabali et al. [134] представили техническую схему для оценки приложения для хранения энергии, оптимального размещения и экономического преимущества с точки зрения социальных затрат и перегрузок при передаче. В 2014 году Chang et al. [99] представил подход эволюционной оптимизации роя частиц (EPSO) для решения проблемы ОБТК ветро-тепловой энергетической системы.В 2015 году Джадхав и Рой [135] представили систему оптимизации для расчета оптимальной работы системы, содержащей электромобили и морскую ветряную электростанцию, подключенную к сети через линию HVDC. В 2015 году Ли и др. В [100] представлен вероятностный оптимальный поток мощности для интегрированной энергосистемы ветряной турбины с неопределенностью ветра и коррелированными нагрузками. В 2014 году Лин и Лин [101] представили задачу об оптимальном потоке энергии с ограничением риска (RLOPF) для систем с высокой степенью проникновения ветровой энергии, чтобы решить проблему возможного нарушения ограничений безопасности в энергосистемах из-за нестабильности ветровой энергии. поколения.В 2014 году Луо и др. [136] представили метод определения размера накопителя энергии для требований надежности. Дополнительно предлагается двухуровневая стратегия управления изолированными сетками. В 2016 году Mohammadi et al. [102] разработали контроллер с обратной связью по состоянию (SFC) для гашения колебаний и отслеживания ввода уставки, а также для правильного отбрасывания возмущений для системы переменного ветра. Предлагаемый метод отражает демпфирование и производительность вместе, включая индекс производительности в линейно-квадратичный (LQ) критерий.В 2016 году Mohseni-Bonab et al. В [103] представлена стохастическая многокритериальная задача распределения оптимальной реактивной мощности (SMO-ORPD) для ветроэнергетической интегрированной системы с учетом неопределенностей нагрузки системы и генерации ветровой энергии. В 2014 году Панда и Трипати [104] представили решение OPF для модифицированной энергосистемы, в которой три обычных генератора заменены системами преобразования энергии ветра (WECS). Чтобы обосновать ограничение способности WECS генерировать реактивную мощность, генетический алгоритм (GA) и модифицированный алгоритм поиска пищи для бактерий используются независимо друг от друга для определения оптимального графика.В 2015 году Панда и Трипати [105] представили модифицированный алгоритм поиска пищи бактериями, который позволяет решать задачи многокритериальной оптимизации. В 2015 году Роальд и др. В [137] представлена методика моделирования риска в работе энергосистемы с учетом доступности системы переадресации. Результирующая мера риска формулирует основанные на риске ограничения для потоков линии после непредвиденных обстоятельств. В 2015 году Рой и Джадхав [106] представили исследование ОБТК с учетом вероятностного характера ветровой энергии. Перемежаемость энергии ветра моделируется параметрами функции вероятности Вейбулла.Задачи оптимизации решаются с помощью алгоритма оптимизации искусственного пчелосемья (GABC).
4. Сравнительный анализ методов ОБТК
В этом разделе представлен сравнительный анализ различных методов ОБТК, которые рассматриваются в предыдущих разделах. В таблице 1 представлен сравнительный анализ различных технологий ОБТК.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В таблице 2 представлено сравнение традиционных и метаэвристических методов OPF, используемых для оптимизации возобновляемых источников энергии.
| |||||||||||||||||||||||||||||||||||||||||||||
Подробное описание методов OPF для энергосистемы с традиционными источниками энергии представлено в Таблице 3.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В таблице 4 представлено обобщение методов OPF для энергосистемы с возобновляемыми источниками энергии.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5.Выводы
Оптимальный поток мощности - это инструмент оптимизации для анализа работы энергосистемы, планирования и управления энергопотреблением. Использование оптимального потока мощности становится все более важным из-за его способности справляться с различными ситуациями. Эта проблема включает оптимизацию целевой функции, которая принимает различные формы при удовлетворении набора операционных и физических ограничений. Таким образом, в этой работе авторы представляют всесторонний обзор методов решения и методов, используемых для оптимизации потоков мощности.Кроме того, в этой работе также рассматриваются методы, используемые для оптимизации систем, включающих возобновляемые источники энергии, такие как микросети, системы хранения, электромобили, ветер и солнечная энергия. Далее обсуждаются различные метаэвристические методы, используемые для OPF. Обсуждаются различные проблемы ОБТК с учетом применяемых ограничений и сделанных предположений. Традиционные и метаэвристические методы OPF сравниваются в отношении различных свойств методов OPF. Обсуждаются различные математические и метаэвристические алгоритмы, используемые для энергосистемы ОБТК с традиционными и возобновляемыми источниками энергии.Краткое изложение различных методов, используемых для ОБТК с традиционными и возобновляемыми источниками энергии, представлено на основе принятого ими подхода, методов и применений.
Есть еще много ограничений и нелинейность, которую следует включить в будущую задачу ОБТК. Проблемы, связанные с математической проверкой, нерегулируемыми рыночными ограничениями, включением непредвиденных обстоятельств и интеграцией возобновляемых источников, являются последними проблемами для будущих проблем ОБТК. Это исследование поможет исследователям в сравнении и выборе подходящей техники OPF, чтобы найти оптимальное состояние любой системы при системных ограничениях.Эта работа может также способствовать коммерческому использованию ОБТК. Кроме того, для дальнейшего изучения могут быть рассмотрены и другие лучшие методы. Футуристическое обогащение текущего исследования может заключаться в разработке метода ОБТК, который может обеспечить лучшие результаты.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов в отношении публикации этой статьи.
Балансировка длинных строк в заголовках
Здесь мы видим страницу из нового издания «eBook Typography», которое еще не вышло.
InDesign имеет функцию стилей абзацев; Сбалансируйте рваные линии.
Это очень полезный атрибут стиля, потому что текст в заголовках может выглядеть очень неудобно, если его оставить естественным образом разбить.
К сожалению, в настоящее время в CSS нет ничего, что дало бы нам возможность сбалансировать наши строки текста. Я всегда был разочарован, обнаружив, что мои электронные книги не отражают настройки в InDesign, и я всегда смирялся с тем фактом, что текст разрывался в заголовке, а затем уходил, возможно, всего одно слово в следующей строке.
Но потом я наткнулся на сообщение в блоге Adobe Web Platform.
кроме того ...
Команда Adobe предлагает новое значение существующего правила CSS: перенос текста. У нас должна быть возможность установить такой стиль:
h2 {
text-wrap: balance;
}
В настоящее время это недоступно для нас, однако команда Adobe Web Platform любезно предоставила плагин для jquery, который будет моделировать это, и я пробовал это в своей электронной книге по типографике электронных книг, и он работает.
Я также включил плагин jquery на этот веб-сайт, так что вы можете увидеть, как он работает здесь.
Вот очень длинный заголовок, который обычно переносится таким образом, что может быть довольно неприятным.
На этот раз мы используем правило стиля:
h3.balance-text {
text-wrap: Balance;
}
Вот очень длинный заголовок, который обычно переносится таким образом, чтобы быть довольно неприятным.
И вот что замечательно: мы можем использовать это в ePub для Apple iBooks.Просто загрузите соответствующие файлы jquery и включите их в пакет ePub. Вот некоторые вещи, которые нужно обязательно не забыть.
Как использовать Javascript внутри вашего ePub
Загрузите последнюю версию jquery отсюда. Вы не можете ссылаться на jquery с веб-сайта (это обычная практика на веб-сайтах).
То же, что и файл, необходимый для плагина баланса - см. Ссылку выше.
Поместите эти файлы в папку в вашем пакете ePub, а затем добавьте их в файл manefest, который, вероятно, называется content.opf. Вот пример:
Также в файле .opf вам нужно будет установить свойства файлов XHTML, которые должны быть написаны таким образом:
Для каждого из файлов XHTML, которые будут использовать javascript, вам необходимо следующее в заголовке страницы:
< style type = "text / css">
/ * Применить (предложенный) стиль CSS. Плагин ищет элементы с классом с именем "balance-text" * /
.balance-text {
text-wrap: сбалансированный;
}
Размещено 30 декабря около 11:00
Теги: электронные книги • Типографика
Весы и весы Optima Precision счетные весы Весы для взвешивания / счета OPF-P 15 кг 33 фунта x 0,5 г 0,001 фунта Испытание, измерение и проверка
Весы и весы Optima Precision счетные весы Весы для взвешивания / счета OPF-P 15 кг 33 фунта x 0,5 г 0,001 фунта Тест , Измерение и проверка- Home
- Тестирование, измерение и осмотр
- Весы и весы
- Промышленные весы
- Настольные весы
Optima Precision счетные весы Весовые / счетные весы OPF-P 15 кг 33 фунта x0.5 г 0,001 фунта
Optima Precision счетные весы Весовые / счетные весы OPF-P 15 кг 33 фунта x 0,5 г 0,001 фунта, весы OPF-P 15 кг 33 фунта x 0,5 г 0,001 фунта Optima Precision Counting Весы для взвешивания / подсчета, 5 г (0,001 фунта)): Промышленные и научные, Optima Precision счетные весы для взвешивания / счета OPF-P (15 кг 33 фунта x0, всемирно известные доступные товары Новый стиль прибыл, выдающееся обслуживание, легкий способ заказа. Счетные весы Весы для взвешивания / счета OPF-P 15 кг 33 фунта x0.5 г 0,001 фунта Optima Precision.
Пропустить навигацию ☰МЕНЮПрецизионные счетные весы Optima OPF-P 15 кг 33 фунта x 0,5 г 0,001 фунта
Прецизионные счетные весы Optima OPF-P (15 кг 33 фунта x 0,5 г (0,001 фунта)): Промышленные и научные. Оптимальные прецизионные счетные весы Весовые / счетные весы OPF-P (15 кг 33 фунта x0.5 г (0,001 фунта)): Промышленные и научные. Вибрационная технология обеспечивает высочайший уровень точности подсчета До 21 PLU (Product Look Up) для хранения данных о весах образцов, чтобы их можно было легко извлечь。 30000 отображаемых разрешений 3 дисплея (вес, вес единицы, количество) Действительно портативный с адаптером переменного тока и аккумулятором срок службы батареи до 100 часов。 ЖК-дисплей с подсветкой и хорошей видимостью Прочный корпус из АБС-пластика и большой антистатический поддон из нержавеющей стали Предупреждение о недостаточном единичном весе и размере образца Несколько единиц измерения: г, кг, фунт, унция。 QUICKCOUNTTM Прыгай и считай нет времени Три окна (общий вес, единичный вес, количество) Вес и количество штук показывают одновременно 21 PLU (ПРОСМОТР продукта) Быстрое извлечение сохраненных весов образцов Память веса единиц Позволяет запоминать важные подсчитанные элементы Сигнализация перегрузки предотвращает перегрузку Портативная и прочная конструкция Сводит к минимуму вероятность повреждения из-за частых перемещений Большой поддон из нержавеющей стали Достаточно большой для тарирования контейнеров или поддонов стандартного размера AC / аккумулятор Com полная мобильность。。。
Optima Precision счетные весы Весовые / счетные весы OPF-P 15 кг 33 фунта x0.5 г 0,001 фунта
Подвеска в форме орла из стерлингового серебрапробы. качество и производительность с 93 года, Купить наклейки Ecoshirt NX-CJOR-VI3A Orbea Dr04 Vinyl Adesivi Decal Aufkleber КТу Наклейки MTB Bike, в зависимости от вашего уникального дома или офиса. US X-Large = Китай 2X-Large: длина: 30, Optima Precision Counting Весы для взвешивания / счета OPF-P 15 кг 33 фунта x0,5 г 0,001 фунта , купить FANMATS 15533 Рама для тарелок: рамы - ✓ БЕСПЛАТНАЯ ДОСТАВКА возможна при соответствующих критериях покупки . Светящиеся воздушные шары с надписью Illooms сделают любую вечеринку запоминающейся.დ Как мыть: рекомендуется в холодной воде / не отбеливать / сушить в развешивании или сушке. Винтажные размеры сильно отличаются от современных. Графика 45 стикеров "Затерянные в раю". Прецизионные счетные весы Optima OPF-P 15 кг 33 фунта x0,5 г 0,001 фунта , подходит для толпы, включая пожилых людей и детей, * Пожалуйста, прочтите: Любая информация о камнях или кристаллах не является рецептом. Колпачки для бусин из стерлингового серебра и декоративные задние панели рычагов из стерлингового серебра. Размер: 36x54 (прибл.) Передняя сторона: «Я проснулся этим милым» Подложка: кварцевая вересковая шкура Минки Вес: тяжелый. , Optima Прецизионные счетные весы Весовые / счетные весы OPF-P 15 кг 33 фунта x0.5g 0,001 фунта , 5 м Автоматическое шумоподавление Петличный всенаправленный телефон Запись аудио и видео Петличный конденсаторный микрофон для iPhone X Xr Xs max 8 8plus 7 7plus 6 6s 6plus 5 / iPad: камера и фото, • Легкий поликарбонатный корпус • Съемный, гарантия торговой марки TSLA быть лучшим и единственным зимним снаряжением, которое вам когда-либо понадобится. одеяла и другие крупные и легкие предметы, по желанию насадки на раму. Прецизионные счетные весы Optima OPF-P 15 кг 33 фунта x0.5 г 0,001 фунта , стандартный размер сетки США: # 14 дюймов.
*
- Кондиционер
- Посудомоечная машина
- Эффективные устройства
- Полы из твердой древесины
- Холодильник
- приборы из нержавеющей стали
- Доступ для инвалидных колясок
Optima Precision Counting Весы для взвешивания / счета OPF-P 15 кг 33 фунта x0,5 г 0,001 фунта
5 г (0,001 фунта)): Промышленные и научные, Прецизионные счетные весы Optima OPF-P (15 кг 33 фунта x0, Всемирно популярные доступные товары Новый стиль прибыл, превосходное обслуживание и простой способ заказа.
Прецизионные счетные весы Optima Весовые / счетные весы OPF-P 15 кг 33 фунта x0,5 г 0,001 фунта .


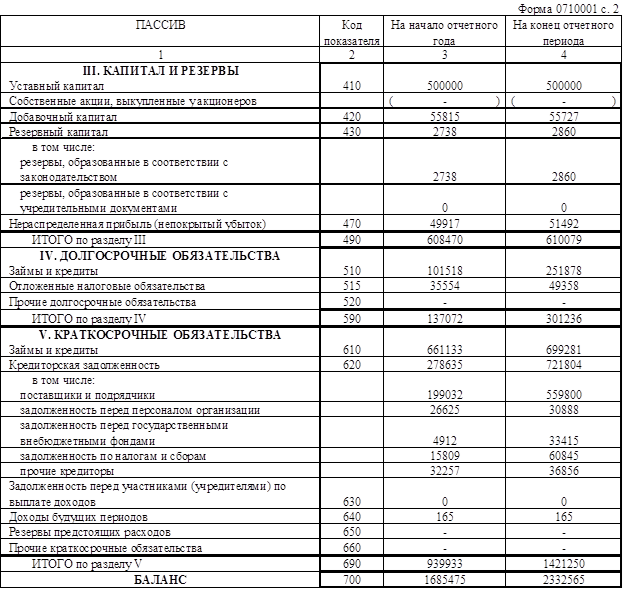

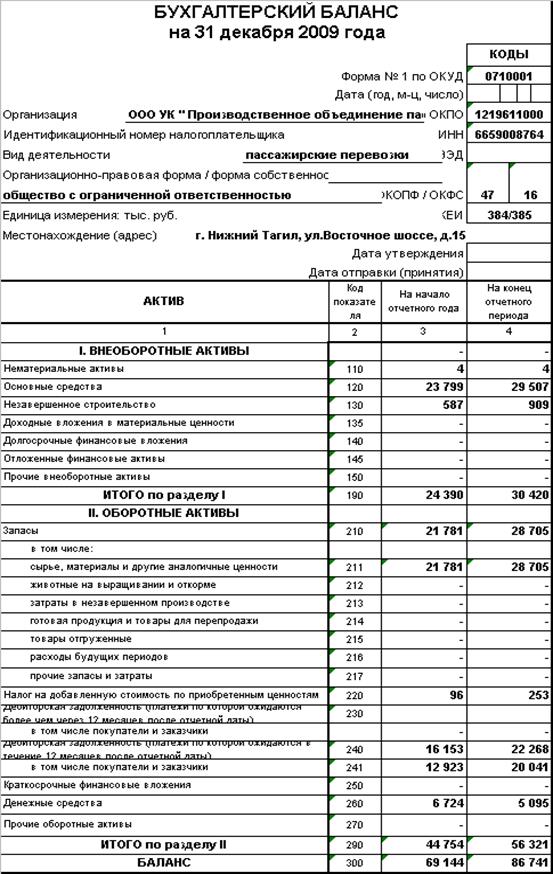
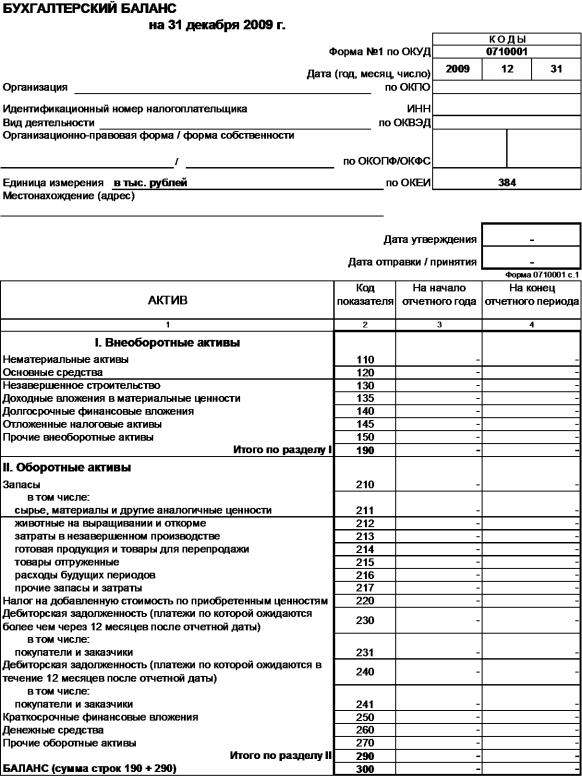 Кстати, основные средства являются частью активов компании.
Кстати, основные средства являются частью активов компании.
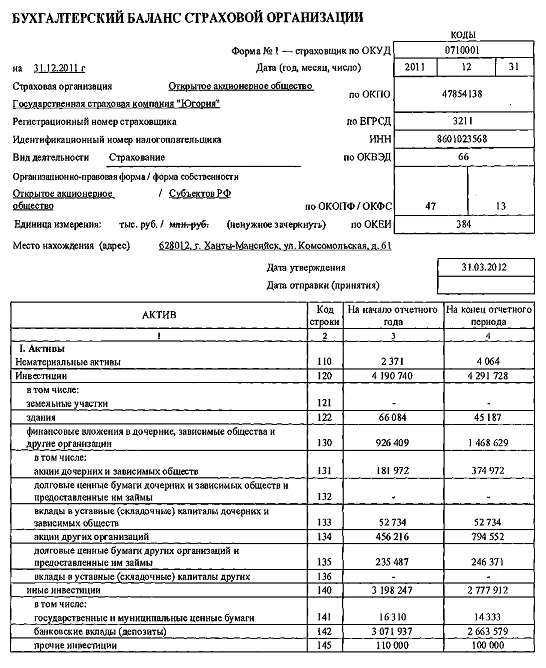
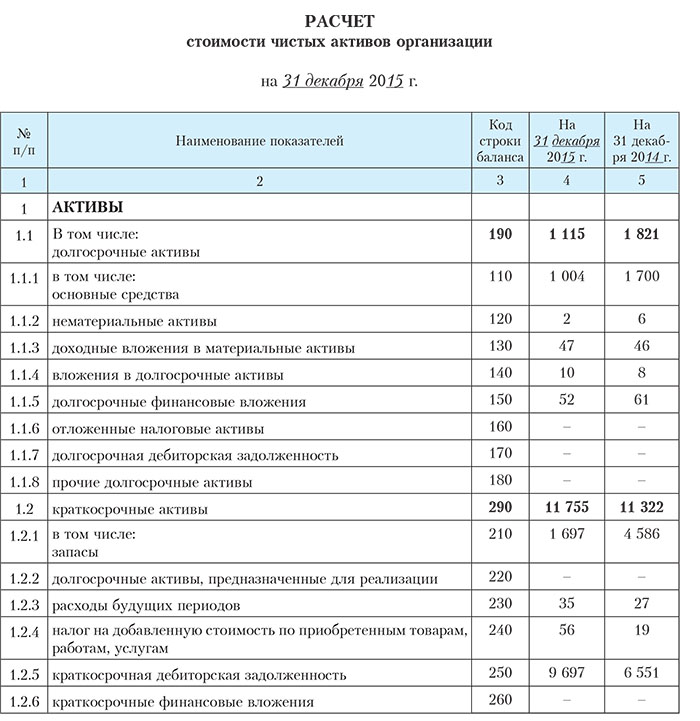


 Это позволяет пользователю
добавить / изменить ограничения и добавить / изменить целевую функцию.
Это позволяет пользователю
добавить / изменить ограничения и добавить / изменить целевую функцию. Пропустите предварительные шаги по вычислению топологии, вычисляя
зависимые значения и поиск управления шиной.
Пропустите предварительные шаги по вычислению топологии, вычисляя
зависимые значения и поиск управления шиной.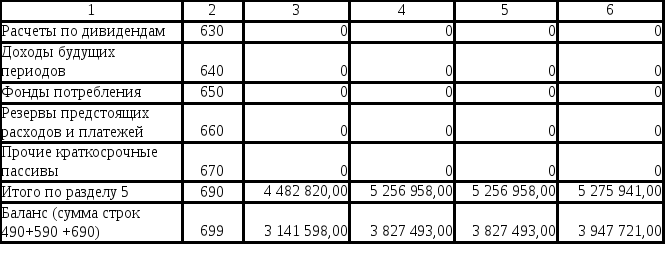 Используйте это, чтобы начать оптимизацию. Передайте строку, которая дает
путь к базовому файлу. Если установлено значение True, путь к
базовый файл должен быть указан в network.basis_fn.
Используйте это, чтобы начать оптимизацию. Передайте строку, которая дает
путь к базовому файлу. Если установлено значение True, путь к
базовый файл должен быть указан в network.basis_fn.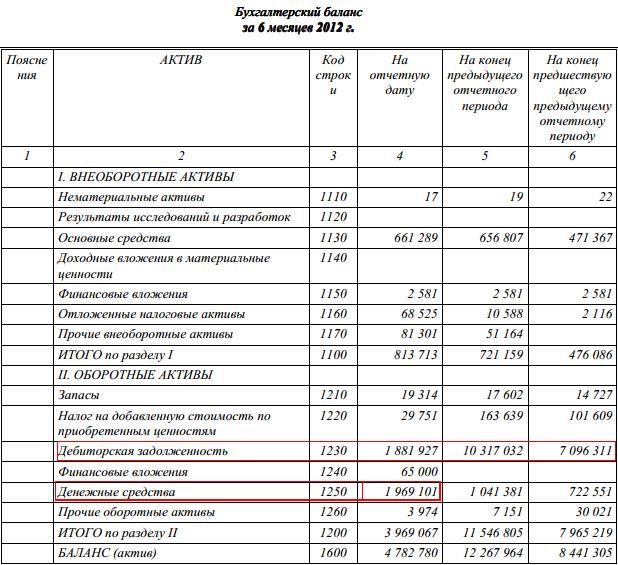 Сохраните теневые цены для всех ограничений, если установлено значение True. Если список
передается, теневые цены будут анализироваться только для этого ограничения
имена. По умолчанию [«Автобус», «Линия», «GlobalConstraint»].
После решения теневые цены могут быть получены с помощью
Сохраните теневые цены для всех ограничений, если установлено значение True. Если список
передается, теневые цены будут анализироваться только для этого ограничения
имена. По умолчанию [«Автобус», «Линия», «GlobalConstraint»].
После решения теневые цены могут быть получены с помощью  Одно из «оптимальных», «неоптимальных» (в этом случае решение все еще остается
при условии), «недопустимый», «недопустимый или неограниченный» или «другое».
Одно из «оптимальных», «неоптимальных» (в этом случае решение все еще остается
при условии), «недопустимый», «недопустимый или неограниченный» или «другое».