Расчет чистой текущей стоимости проекта — Студопедия
| Статья доходов/расходов | 1-ый год | 2-ой год | 3-ий год | 4-ый год | 5-ый год | Итого | Среднемесячная сумма, грн. | |
| Доход (выручка от реализации) | 3 409 831 | 4 780 932 | 4 755 722 | 4 755 722 | 4 755 722 | 22 517 930 | 402 106 | |
| Расходы | 2 660 964 | 3 658 611 | 3 651 844 | 3 644 341 | 3 637 901 | 17 253 621 | 308 100 | |
| Прибыль | 748 907 | 1 122 321 | 1 123 878 | 1 131 382 | 1 137 821 | 5 264 309 | 94 006 | |
| Денежный поток (прибыль+амортизация) | 808 086 | 1 198 679 | 1 188 248 | 1 188 248 | 1 188 248 | 5 571 510 | 99 491 | |
| Возврат денежных средств инвестору | 515 578 | 719 207 | 712 949 | 712 949 | 712 949 | 3 373 632 | 60 243 | |
| Поступление инвестиций | 1 162 875 | 14 417 | 15 892 | 25 732 | 15 892 | 1 234 809 | 20 580 | |
| Ставка дисконтирования | 10% | |||||||
| Фактор дисконта | 0,909 | 0,826 | 0,751 | 0,683 | 0,621 | - | — | |
| Дисконтированный денежный поток PVt | 750 459 | 1 027 481 | 925 601 | 841 456 | 764 960 | 4 309 956 | 71 833 | |
| Дисконтированные инвестиции | 1 132 294 | 12 882 | 12 914 | 18 845 | 10 673 | 1 187 609 | 19 793 | |
| NPV | 3 122 347 | |||||||
Как видно из таблицы, срок реализации проекта 5 лет.
В данной таблице приведены укрупненные ежегодные данные, но планировать затраты и доходы следует ежемесячно.
Фактор дисконта рассчитывается как:
Далее необходимо произвести расчет среднегодового размера чистой прибыли по проекту, которая определяется по формуле, который определяется по формуле:
где Пt – размер чистой прибыли, полученной предприятием от реализации проекта в t-том году;
n – длительность реализации проекта, лет.
Для данного примера среднегодовой размер чистой прибыли составит: 5 264 309 / 5 = 1 052 861,8 грн.
Индекс доходности инвестиций является относительным показателем эффективности проекта и характеризует размер суммарного денежного потока, приходящийся на единицу инвестиционных ресурсов (с учетом фактора времени):
Данный показатель тесно связан с показателем NPV, однако он характеризует не абсолютное, а относительное превышение приведенного денежного потока по проекту над приведенными инвестициями.
Если PI>1, проект следует принять.
Индекс доходности для данного примера составит:
PI = 4 309 956 / 1 187 609 = 3,63 грн./1 грн.
Внутренняя норма рентабельности (IRR) равна норме дисконтирования, при которой чистая текущая стоимость проекта равна 0. В какой-то степени данный показатель характеризует устойчивость проекта к воздействию внешних факторов (например, к росту процентной ставки, уровню инфляции) и определяет верхнюю границу нормы дисконта, при которой проект еще может быть принят. Наиболее точным методом определения IRR является метод прямого подбора.
Внутренняя норма рентабельности для данного примера – 137%.
Показатель дисконтированного срока окупаемости инвестиций характеризует средний срок, в течение которого инвестиции в данный проект окупятся за счет приведенного денежного потока:
где n – продолжительность реализации проекта, лет.
DPP= 1 187 609/(4 309 956:5)= 1,38 лет = 16,5 месяцев
Обычный срок окупаемости инвестиций – это период, в течение которого инвестиции в данный проект окупятся за счет чистой прибыли (без дисконтирования, т.
е. учета фактора времени):
Обычный срок окупаемости для данного примера равен:
Ток = 5 264 309 / 1 234 809 = 1,17 лет = 14,1 мес.
В целом показатели эффективности реализации проекта для данного примера представлены в следующей таблице:
9.2. Схема расчета чистой текущей стоимости.
Метод чистой текущей стоимости позволяет классифицировать проекты и принимать инвестиционные решения на основе сравнения затрат с доходами по инвестиционному проекту, приведенными к текущей стоимости.Схема расчета показателя чистой текущей стоимости (NPV):
1. Определить текущую стоимость каждой суммы потока доходов, исходя из ставки дисконтирования и периода возникновения доходов.
2. Суммировать приведенные доходы по проекту.
3.
Сравнить суммарные приведенные доходы
с величиной затрат по проекту.
NPV = ПД-ПР
где ПД – суммарные приведенные доходы,
ПР – приведенные затраты по проекту.
4. Проекты, имеющие отрицательную величину NPV, инвестор отклоняет. При рассмотрении нескольких вариантов предпочтение отдается проекту с максимальной величиной данного показателя.
Рассчитываем показатель NPV по анализируемому проекту «Уран». R=15%
Период | 0 | 1 | 2 | 3 | 4 | 5 |
Денежный поток | (1000) | 200 | 500 | 600 | 800 | 900 |
Дисконтированный денежный поток | (1000) | 174 | 378 | 394 | 458 | 447 |
NPV | -1000+174+378+394+458+447=851 | |||||
Положительная
величина NPV показывает, насколько
возрастет стоимость активов инвестора
от реализации данного проекта.
Поэтому предпочтение
отдается проекту с наибольшей величиной
чистой текущей стоимости доходов.
Показатель NPV относится к категории абсолютных, что позволяет суммировать результаты по отобранным проектам для определения NPV по инвестиционному портфелю в целом.
Недостатки данного показателя:
Во-первых, абсолютное значение NPV при сравнительном анализе инвестиционных проектов не учитывает объема вложений по каждому варианту.
Во-вторых, величина NPV по проекту зависит не только от суммы затрат и распределения потока доходов во времени. На результаты существенное влияние оказывает применяемая аналитиками ставка дисконтирования, а оценка уровня риска проводится достаточно субъективно.
Рассмотрим влияние ставки дисконтирования на доходность проекта «Уран».
Ставка дисконтирования, % | 5 | 15 | 25 | 35 | 45 |
Чистая текущая стоимость (NPV) | + 1526 | + 851 | + 410 | + 108 | — 106 |
Увеличение ставки
дисконта снижает величину NPV.
Следовательно,
один и тот же проект в разных условиях,
при разной ставке дисконтирования, даст
различные результаты и из прибыльного
может превратиться в убыточный.
9.3. Период окупаемости.
Период окупаемости определяется как ожидаемое число лет, необходимое для полного возмещения инвестиционных затрат. Период окупаемости рассчитывается следующим образом:
Период окупаемости = число лет, предшествующих году окупаемости + Невозмещенная стоимость на начало года окупаемости / Денежный поток в течение года окупаемости
Рассмотрим методику расчета показателя на условном примере. Инвестиционный проект «Уран» требует вложения 1000, прогнозируемый поток доходов составит: 1 год – 200; 2 год – 500, 3 год – 600, 4 год – 800, 5 год – 900. Ставка дисконтирования – 15%.
Статический метод
говорит о том, что проект окупится через
3,5 года. Однако этот срок не учитывает
требуемую норму дохода на инвестиции
в конкретной сфере.
Схема расчета срока окупаемости.
Рассчитать дисконтированный денежный поток доходов по проекту, исходя из ставки дисконтирования и периода возникновения доходов.
Рассчитать накопленный дисконтированный денежный поток (нарастающим итогом).
Накопленный дисконтированный денежный поток рассчитывается до получения первой положительной величины.
Определить срок окупаемости по формуле.
Рассчитаем срок окупаемости проекта «Уран».
Период | 0 | 1 | 2 | 3 | 4 | 5 |
Денежный поток | (1000) | 200 | 500 | 600 | 800 | 900 |
Дисконтированный денежный поток (R=15%) | (1000) | 174 | 378 | 394 | 458 | 447 |
Накопленный дисконтированный денежный поток | -1000 | -826 | -448 | -54 | +404 |
|
Период окупаемости = 4 + 54 / 458 = 4,1 года | ||||||
Таким образом
период, реально необходимый для возмещения
инвестированной суммы, с учетом фактора
времени на 0,6 года больше срока,
определенного статическим методом.
Данный показатель определяет срок, в течение которого инвестиции будут «заморожены», т. к. реальный доход от инвестиционного проекта начнет поступать только по истечении периода окупаемости. При отборе вариантов предпочтение отдается проектам с наименьшим сроком окупаемости.
Период окупаемости целесообразно рассчитывать по проектам, финансируемым за счет долгосрочных обязательств. Срок окупаемости по проекту должен быть короче периода пользования заемными средствами, устанавливаемого кредитором.
Показатель является приоритетным в том случае, если для инвестора главным является максимально быстрый возврат инвестиций, например выбор путей финансового оздоровления обанкротившихся предприятий.
Недостатки данного показателя:
Во-первых,
в расчетах игнорируются доходы, получаемые
после предлагаемого срока окупаемости
проекта. Следовательно, при отборе
альтернативных проектов можно допустить
серьезные просчеты, если ограничиваться
применением только данного показателя.
Во-вторых, использование этого показателя для анализа инвестиционного портфеля в целом требует дополнительных расчетов. Период окупаемости инвестиций по портфелю в целом не может быть рассчитан как простая средняя величина.
Метод расчета чистой текущей стоимости (чистого приведенного эффекта) (net present value — NPV)
Показатель чистой текущей стоимости является производным от показателя текущей стоимости. Под текущей стоимостью (present value — PV) понимается стоимость будущих поступлений денежных средств (future value — FV), отнесенная к настоящему моменту с помощью процедуры дисконтирования. Показатель PV можно рассчитать по формуле, описывающей простую финансовую операцию: размещение денежных средств на условиях срочности, платности, возвратности с единовременным погашением:
PV + r • PV = FV,
где PV — сумма денежных средств, предназначенных для размещения на условиях срочности, платности, возвратности;
r — процентная ставка, являющаяся платой за предоставленные в кредит денежные средства;
FV — сумма погашения кредита, включающая первоначальную сумму долга и проценты.
Преобразование вышеприведенной формулы простой финансовой операции позволит получить формулу расчета показателя текущей стоимости:
PV + r • PV = FV;
PV (1 + r) = FV;
PV= FV / 1+ r = FV 1 / 1 + r;
PV = FV 1 / 1+r.
Если погашение кредита с процентами происходит частями в течение нескольких лет (или частями в течение нескольких лет
поступают доходы от проекта), то формула расчета текущей стоимости будет иметь следующий вид:
Под чистой текущей стоимостью (net present value — NPV) понимается разница между общей суммой дисконтированных потоков будущих поступлений денежных средств, генерируемых данным проектом, и общей суммой инвестиций (invest cost — IС).
где ? FVn — общая сумма будущих поступлений от проекта;
r — доходность проекта;
IС — сумма инвестиций.
Показатель чистой текущей стоимости (NPV) представляет собой разность между совокупными доходами от проекта и совокупными расходами, связанными с проектом.
Разность может быть больше нуля, равна нулю или меньше нуля.
Если:
NPV > 0, то проект следует принять;
NPV = 0, то проект является ни прибыльным, ни убыточным;
NPV < 0, то проект следует отвергнуть.
Приведенная стоимость — Present value
Экономическое понятие, обозначающее величину ожидаемого потока доходов, определяемую на дату оценки.
В экономике и финансах , приведенная стоимость ( PV ), также известная как дисконтированная стоимость , является значением ожидаемого потока дохода , определенного по состоянию на дату оценки. Приведенная стоимость обычно меньше будущей стоимости, потому что деньги имеют процентный потенциал, характеристика, называемая временной стоимостью денег , за исключением периодов нулевых или отрицательных процентных ставок, когда приведенная стоимость будет равна или больше будущая стоимость. Временную стоимость можно описать упрощенной фразой: «Сегодня доллар стоит больше, чем доллар завтра».
Здесь «стоит больше» означает, что его ценность выше. Доллар сегодня стоит больше, чем доллар завтра, потому что доллар можно инвестировать и заработать дневные проценты, в результате чего общая сумма будет накапливаться до стоимости, превышающей доллар к завтрашнему дню. Проценты можно сравнить с арендной платой. Подобно тому, как арендная плата выплачивается арендодателю арендатором без права собственности на передаваемый актив, так и проценты кредитору выплачиваются заемщиком, который получает доступ к деньгам на некоторое время, прежде чем выплатить их обратно. Предоставляя заемщику доступ к деньгам, кредитор жертвует меновой стоимостью этих денег и получает за это компенсацию в виде процентов. Первоначальная сумма заемных средств (текущая стоимость) меньше общей суммы денег, выплаченных кредитору.
Расчеты текущей стоимости, а также расчеты будущей стоимости используются для оценки ссуд , ипотечных кредитов , аннуитетов , фондов погашения , бессрочных выплат , облигаций и т.
Д. Эти вычисления используются для сравнения денежных потоков, которые не происходят одновременно, поскольку даты должны быть согласованы, чтобы можно было сравнивать значения. При выборе между проектами, в которые вкладывать средства, выбор может быть сделан путем сравнения соответствующих приведенных стоимостей таких проектов путем дисконтирования ожидаемых потоков доходов по соответствующей процентной ставке проекта или норме прибыли. Следует выбирать проект с наибольшей текущей стоимостью, то есть наиболее ценный на сегодняшний день.
Покупка лет
Традиционный метод оценки будущих потоков доходов как суммы текущего капитала заключается в умножении среднего ожидаемого годового денежного потока на коэффициент, известный как «покупка за годы». Например, при продаже третьей стороне имущества, сданного в аренду арендатору по договору аренды на 99 лет с арендной платой в размере 10 000 долларов в год, сделка может быть заключена на условиях «20-летней покупки», в результате чего стоимость аренды составит 20 * 10 000 долларов США, т.
е. 200 000 долларов США. Это приравнивается к дисконтированной приведенной стоимости на неограниченный срок по ставке 5%. Для более рискованных инвестиций покупатель потребует оплатить меньшее количество лет покупки. Этот метод использовался, например, английской короной при установлении перепродажных цен на поместья, захваченные при роспуске монастырей в начале 16 века. Стандартное использование — покупка на 20 лет.
Задний план
Если предлагается выбор между 100 долларами сегодня или 100 долларами через год, а реальная процентная ставка положительная в течение года, при прочих равных условиях , рациональный человек выберет 100 долларов сегодня. Экономисты называют это временным предпочтением . Временные предпочтения могут быть измерены путем продажи с аукциона безрисковой ценной бумаги, например казначейского векселя США. Если купон на 100 долларов с нулевым купоном, подлежащим выплате в течение одного года, продается сейчас за 80 долларов, то 80 долларов — это приведенная стоимость банкноты, которая через год будет стоить 100 долларов.
Это связано с тем, что деньги можно положить на банковский счет или в любую другую (безопасную) инвестицию, которая принесет проценты в будущем.
У инвестора, у которого есть деньги, есть два варианта: потратить их прямо сейчас или сэкономить. Но финансовая компенсация за их сбережение (а не на их расходование) заключается в том, что денежная ценность будет накапливаться за счет сложных процентов, которые он или она получит от заемщика (банковский счет, на который у него размещены деньги).
Следовательно, чтобы оценить реальную стоимость денежной суммы сегодня по истечении заданного периода времени, экономические агенты складывают сумму денег по заданной (процентной) ставке. В большинстве актуарных расчетов используется безрисковая процентная ставка, которая соответствует минимальной гарантированной ставке, предоставляемой, например, сберегательным счетом банка, при отсутствии риска неисполнения обязательств банком для своевременного возврата денег держателю счета. Для сравнения изменения покупательной способности следует использовать реальную процентную ставку ( номинальная процентная ставка минус уровень инфляции ).
Операция преобразования текущей стоимости в будущую стоимость называется капитализацией (сколько сегодня будут стоить 100 долларов через 5 лет?). Обратная операция — оценка приведенной стоимости будущей суммы денег — называется дисконтированием (сколько 100 долларов, полученных через 5 лет, например, в лотерее, будут стоить сегодня?).
Отсюда следует, что если кто-то должен выбирать между получением 100 долларов сегодня и 100 долларов через год, рациональным решением будет выбрать 100 долларов сегодня. Если деньги должны быть получены в течение одного года и предполагаемая процентная ставка по сберегательному счету составляет 5%, человеку необходимо предложить не менее 105 долларов в год, чтобы два варианта были эквивалентны (либо получение 100 долларов сегодня, либо получение 105 долларов за один год. год). Это связано с тем, что если на сберегательный счет депонируется 100 долларов, через год его стоимость составит 105 долларов, опять же без риска потери первоначальной суммы из-за дефолта банка.
Процентные ставки
Проценты — это дополнительная сумма денег, полученная между началом и концом периода времени. Проценты представляют собой временную стоимость денег и могут рассматриваться как рента, необходимая заемщику для использования денег кредитора. Например, когда физическое лицо берет ссуду в банке, с него взимаются проценты. Или же, когда физическое лицо кладет деньги в банк, деньги приносят проценты. В этом случае банк является заемщиком средств и несет ответственность за зачисление процентов владельцу счета. Аналогичным образом, когда физическое лицо инвестирует в компанию (через корпоративные облигации или через акции ), компания заимствует средства и должна выплачивать частному лицу проценты (в форме купонных выплат, дивидендов или повышения курса акций). Процентная ставка — это изменение суммы денег, выраженное в процентах, в течение одного периода начисления сложных процентов. Период начисления сложных процентов — это период времени, который должен пройти, прежде чем проценты будут начислены или добавлены к общей сумме.
Например, проценты, начисляемые ежегодно, начисляются один раз в год, а период начисления сложных процентов составляет один год. Проценты, начисляемые ежеквартально, начисляются четыре раза в год, а период начисления сложных процентов составляет три месяца. Период начисления процентов может быть любой продолжительности, но некоторые общие периоды — год, полгода, квартал, месяц, день и даже непрерывно.
С процентными ставками связано несколько типов и условий :
- Сложный процент , процент, который экспоненциально увеличивается в последующие периоды,
- Простой интерес , дополнительный интерес, который не увеличивается
- Эффективная процентная ставка , эффективный эквивалент по сравнению с несколькими периодами сложных процентов
- Номинальная годовая процентная ставка , простая годовая процентная ставка нескольких процентных периодов
- Ставка дисконтирования , обратная процентная ставка при выполнении расчетов в обратном порядке
- Непрерывно начисленные проценты , математический предел процентной ставки с нулевым периодом времени.
- Реальная процентная ставка , учитывающая инфляцию.
Расчет
Операция по оценке существующей суммы денег когда-нибудь в будущем называется капитализацией (сколько 100 будет стоить сегодня через пять лет?). Обратная операция — оценка приведенной стоимости будущей суммы денег — называется дисконтированием (сколько 100, полученных через пять лет, будут стоить сегодня?).
Таблицы обычно предлагают функции для вычисления текущей стоимости. В Microsoft Excel есть функции приведенной стоимости для разовых платежей — «= ЧПС (…)» и серии равных периодических платежей — «= ПС (…)». Программы будут гибко рассчитывать приведенную стоимость для любого денежного потока и процентной ставки или для графика различных процентных ставок в разное время.
Текущая стоимость единовременной выплаты
В наиболее часто применяемой модели текущей оценки используются сложные проценты . Стандартная формула:
- пVзнак равноC(1+я)п{\ Displaystyle PV = {\ гидроразрыва {C} {(1 + i) ^ {n}}} \,}
Где будущая сумма денег, которая должна быть дисконтирована, — это количество периодов начисления сложных процентов между текущей датой и датой, когда сумма стоит , — это процентная ставка за один период начисления сложных процентов (конец периода начисления сложных процентов наступает, когда начисляются проценты.
{5}}} = \ $ 620.92 \,}
Интерпретация такова, что при эффективной годовой процентной ставке 10% физическому лицу будет безразлично получить 1000 долларов через пять лет или 620,92 доллара сегодня.
Покупательная способность в сегодняшних деньгах суммы денег, года в будущее, можно вычислить по той же формуле, где в данном случае является предполагаемым будущим уровнем инфляции . C{\ Displaystyle \, С \,}п{\ Displaystyle \, п \,}я{\ Displaystyle \, я \,}
Чистая приведенная стоимость потока денежных потоков
Денежный поток — это сумма денег, которая либо выплачена, либо получена, дифференцированная по отрицательному или положительному знаку, в конце периода. Обычно полученные денежные потоки обозначаются положительным знаком (общая сумма денежных средств увеличилась), а выплачиваемые денежные потоки обозначаются отрицательным знаком (общая сумма денежных средств уменьшилась). Денежный поток за период представляет собой чистое изменение денег за этот период.
{3}}} = 95,24-45,35 + 30,23 = 80,12,}
Следует сделать несколько соображений.
- Периоды могут быть непоследовательными. Если это так, экспоненты изменятся, чтобы отразить соответствующее количество периодов.
- Процентные ставки за период могут быть разными. Денежный поток должен быть дисконтирован с использованием процентной ставки за соответствующий период: если процентная ставка изменяется, сумма должна быть дисконтирована до периода, в котором происходит изменение, с использованием второй процентной ставки, а затем дисконтируется до настоящего времени с использованием первой процентной ставки. . Например, если денежный поток для первого периода составляет 100 долларов, а для второго — 200 долларов, а процентная ставка для первого периода составляет 5%, а для второго — 10%, то чистая приведенная стоимость будет:
- NпVзнак равно100(1.05)-1+200(1,10)-1(1.05)-1знак равно100(1.05)1+200(1,10)1(1.05)1знак равно$95,24+$173,16знак равно$268,40{\ displaystyle NPV = 100 \, (1. {4}} {4}}}
Приведенная стоимость аннуитета
Многие финансовые соглашения (включая облигации, другие ссуды, аренду, заработную плату, членские взносы, аннуитеты, включая немедленную аннуитетную и аннуитетную выплату, линейные амортизационные отчисления) предусматривают структурированные графики платежей; выплаты одинаковой суммы через определенные промежутки времени. Такой порядок называется аннуитетом . Выражения для текущей стоимости таких выплат являются сложениями из геометрической прогрессии .
Существует два типа аннуитетов: немедленная аннуитетная и аннуитетная. Для немедленной аннуитета платежи принимаются (или выплачиваются) в конце каждого периода, временами от 1 до , в то время как для причитающегося аннуитета платежи принимаются (или выплачиваются) в начале каждого периода, временами от 0 до . Эту небольшую разницу необходимо учитывать при расчете приведенной стоимости. п{\ Displaystyle \, п \,}п{\ Displaystyle \, п \,}п{\ Displaystyle \, п \,}п-1{\ Displaystyle \, п-1 \,}
Аннуитет — это немедленный аннуитет с еще одним периодом начисления процентов.
{- n}} {i}} \ right], \ qquad (1)}
{4}} {4}}}
{- n}} {i}} \ right], \ qquad (1)}где:
- п{\ Displaystyle \, п \,} = количество периодов,
- C{\ Displaystyle \, С \,} = сумма денежных потоков,
- я{\ Displaystyle \, я \,} = эффективная периодическая процентная ставка или доходность.
Примерный расчет аннуитета и кредита
Приведенная выше формула (1) для немедленных расчетов аннуитета мало что дает среднему пользователю и требует использования какого-либо вычислительного оборудования. Существует приближение, которое менее пугающе, его легче вычислить и которое дает некоторую информацию для неспециалистов. Это дается
- C≈пV(1п+23я){\ displaystyle C \ приблизительно PV \ left ({\ frac {1} {n}} + {\ frac {2} {3}} i \ right)}
Где, как указано выше, C — аннуитетный платеж, PV — основная сумма, n — количество платежей, начиная с конца первого периода, а i — процентная ставка за период. Эквивалентно C — это периодическое погашение ссуды для ссуды PV, продолжающейся n периодов под процентную ставку, т.
е. Формула верна (для положительных n, i) для ni≤3. Для полноты, при ni≥3 приближение равно .
C≈пVя{\ Displaystyle C \ приблизительно PVi}
Формула может, при некоторых обстоятельствах, свести вычисления к одной только мысленной арифметике. Например, каковы (приблизительные) выплаты по ссуде на сумму PV = 10 000 долларов, выплачиваемую ежегодно в течение n = десяти лет под 15% годовых (i = 0,15)? Применимая приблизительная формула: C ≈ 10 000 * (1/10 + (2/3) 0,15) = 10 000 * (0,1 + 0,1) = 10 000 * 0,2 = 2000 долларов США в год только по ментальной арифметике. Правильный ответ — 1993 $, очень близко.
Общее приближение имеет точность в пределах ± 6% (для всех n≥1) для процентных ставок 0≤i≤0,20 и в пределах ± 10% для процентных ставок 0,20≤i≤0,40. Однако он предназначен только для «грубых» расчетов.
Приведенная стоимость бессрочного права
Вечность относится к периодическим платежам, получение за неопределенное время , хотя несколько таких инструментов существуют.
{k}}} = {\ frac {C} {i}}, \ qquad я> 0,}
которые образуют геометрический ряд .
Опять же, существует различие между бессрочным немедленным платежом, когда платежи получены в конце периода, и бессрочным платежом, полученным в начале периода. И, как и при расчетах аннуитета, бессрочный и немедленный бессрочные платежи различаются на коэффициент : (1+я){\ Displaystyle (1 + я)}
- пVбессрочныйзнак равнопVбессрочность немедленно(1+я){\ displaystyle PV _ {\ text {perpetuity due}} = PV _ {\ text {perpetuity inventory}} (1 + i) \, \!}
PV облигации
- См .: Оценка облигаций # Подход текущей стоимости
Корпорация выпускает облигацию , долговую ценную бумагу, приносящую процентный доход, инвестору для сбора средств. Облигация имеет номинальную стоимость, купонную ставку и дату погашения, что, в свою очередь, дает количество периодов до наступления срока погашения долга, который должен быть погашен. Держатель облигации будет получать купонные выплаты раз в полгода (если не указано иное) в размере , до наступления срока погашения облигации, после чего держатель облигации получит последнюю купонную выплату и номинальную стоимость облигации .
{- п}}
Цена покупки равна номинальной стоимости облигации, если купонная ставка равна текущей рыночной процентной ставке, и в этом случае говорят, что облигация продается «по номинальной стоимости». Если купонная ставка ниже рыночной процентной ставки, цена покупки будет меньше номинальной стоимости облигации, и считается, что облигация была продана «со скидкой» или ниже номинала. Наконец, если купонная ставка выше рыночной процентной ставки, цена покупки будет больше номинальной стоимости облигации, и считается, что облигация была продана «с премией» или выше номинала.
Технические детали
Текущая стоимость аддитивна . Приведенная стоимость связки денежных потоков — это сумма текущей стоимости каждого из них. Смотрите временную стоимость денег для дальнейшего обсуждения. Эти расчеты необходимо применять осторожно, поскольку есть основные предположения:
(Фактически, приведенная стоимость денежного потока при постоянной процентной ставке математически равна одной точке в преобразовании Лапласа этого денежного потока, оцениваемой с помощью переменной преобразования (обычно обозначаемой s), равной процентной ставке.
Полное преобразование Лапласа имеет вид кривая всех приведенных значений, построенная как функция процентной ставки. Для дискретного времени, когда платежи разделены большими периодами времени, преобразование сводится к сумме, но когда платежи происходят почти непрерывно, математика непрерывного функции можно использовать как приближение.)
Варианты / подходы
В основном есть два вкуса Present Value. Когда возникает неопределенность как в сроках, так и в сумме денежных потоков, подход на основе ожидаемой приведенной стоимости часто оказывается подходящим методом.
- Традиционный подход к приведенной стоимости — в этом подходе для оценки справедливой стоимости будет использоваться единый набор предполагаемых денежных потоков и единая процентная ставка (соизмеримая с риском, обычно средневзвешенная стоимость компонентов).
- Подход ожидаемой приведенной стоимости — в этом подходе для оценки справедливой стоимости используются несколько сценариев денежных потоков с различной / ожидаемой вероятностью и безрисковой ставкой, скорректированной с учетом кредита.
Выбор процентной ставки
Используемая процентная ставка представляет собой безрисковую процентную ставку, если в проекте нет рисков. Норма прибыли от проекта должна быть равна или превышать эту норму прибыли, иначе было бы лучше инвестировать капитал в эти безрисковые активы. Если есть риски, связанные с инвестициями, это может быть отражено с помощью премии за риск . Требуемая премия за риск может быть найдена путем сравнения проекта с нормой доходности, требуемой от других проектов с аналогичными рисками. Таким образом, инвесторы могут учитывать любую неопределенность, связанную с различными инвестициями.
Метод оценки по приведенной стоимости
Инвестор, ссудодатель денег, должен решить, в какой финансовый проект вложить свои деньги, и приведенная стоимость предлагает один из методов принятия решения. Финансовый проект требует первоначальных денежных затрат, таких как цена акций или цена корпоративной облигации. Проект требует вернуть первоначальные затраты, а также некоторые излишки (например, проценты или будущие денежные потоки).
Инвестор может решить, в какой проект инвестировать, рассчитав приведенную стоимость каждого проекта (используя одинаковую процентную ставку для каждого расчета), а затем сравнив их. Будет выбран проект с наименьшей приведенной стоимостью — наименьшими начальными затратами, поскольку он предлагает такую же прибыль, как и другие проекты, за наименьшую сумму денег.
Смотрите также
Ссылки
дальнейшее чтение
Анализ эффективности инвестиций
Используемые термины в калькуляторе
Инвестиции — размещение капитала с целью получения прибыли. Инвестиции являются неотъемлемой частью современной экономики. От кредитов инвестиции отличаются степенью риска для инвестора (кредитора) — кредит и проценты необходимо возвращать в оговорённые сроки независимо от прибыльности проекта, инвестиции (инвестированный капитал) возвращаются и приносят доход только в прибыльных проектах. Если проект убыточен — инвестиции могут быть утрачены полностью или частично.
Поток, денежный свободный — денежный поток, которым располагает компания после финансирования всех инвестиций, которые она находит целесообразным осуществить; определяется как прибыль от основной деятельности после уплаты налогов плюс амортизация минус инвестиции.
Ставка дисконтирования — это параметр отражает скорость изменения стоимости денег в текущей экономике. Он принимается равным либо ставке рефинансирования, либо проценту по считающимся безрисковыми долгосрочным государственным облигациям, либо проценту по банковским депозитам. Для расчета инвестиционных проектов этот параметр может приниматься равным планируемой доходности инвестиционного проекта.
Чистый дисконтированный доход (NPV) – это сальдо всех операционных и инвестиционных денежных потоков, учитывающее дополнительно стоимость использованного капитала. NPV проекта будет положительным, а сам проект – эффективным, если расчеты показывают, что проект покрывает свои внутренние затраты, а также приносит владельцам капитала доход не ниже, чем они потребовали (не ниже ставки дисконтирования).
Индекс прибыльности инвестиций (PI) — Показатель иллюстрирует отношение отдачи капитала к размеру вложенного капитала, показатель прибыльности инвестиций показывает относительную прибыльность проекта или дисконтируемую стоимость денежных поступлений от проекта в расчете на единицу вложений. Индекс прибыльности рассчитывается по формуле: PI = NPV / I, где I – вложения.
Внутренняя норма доходности (IRR) — процентная ставка, при которой проект не является ни прибыльным, ни убыточным. Для проектов продолжительностью более двух лет формулы для расчета этого показателя не существует, его можно определить только методом итерации (или при помощи компьютерной программы, использующей данный метод, например, Excel). Возможно определение графическим способом.
Рекомендуемые значения показателей
Чистая приведенная стоимость (NPV) | > 0 – бизнес-проект принимаем; <0 – отказываемся от проекта >= 50% от суммы кредита |
Индекс прибыльности (PI) | > 1 бизнес-проект прибыльный; = 1 — проект не прибыльный; < 1 — проект убыточный |
Внутренняя норма доходности (IRR) | >= процентная ставка по кредиту проекта |
ВАЖНО: Не один из перечисленных показателей эффективности инвестиций не является достаточным для принятия проекта к реализации.
Одновременно важное значение играет соотношение и распределение собственных и привлекаемых средств, а так же другие факторы (наличие предварительных договоренностей на сбыт продукции проекта; денежный поток и возможность погашения обязательств согласно вашему бизнес-плану; срок окупаемости и срок возврата кредита; коэффициент покрытия долга и др.).
Калькулятор чистой приведенной стоимости
- Дом
- Контакт
- Войти
Переключить навигацию
- Финансы
- Инвестиции
- Калькулятор аннуитетов
- Калькулятор APY
- Калькулятор доходности облигаций
- Калькулятор CAGR
- Калькулятор сложных процентов
- Калькулятор IRR
- 9000 Калькулятор чистой стоимости
- 9000 NPY 9000 Калькулятор доходности от аренды
- Калькулятор рентабельности инвестиций
- Калькулятор правила 72
- Калькулятор сбережений
- Простой калькулятор процентов
- Аренда
- Калькулятор аренды автомобиля
- Калькулятор
- AP
- Кредиты
- Ссудный калькулятор
- Калькулятор DTI
- Калькулятор отношения долга к лимиту
- Калькулятор только процентов
- Калькулятор доступности ссуды
- Калькулятор сравнения ссуд
- Ипотечный калькулятор
- Расчет рефинансирования ator
- Инвестиции
- Калькулятор коэффициента наличности
- Калькулятор комиссии
- Калькулятор CPC
- Калькулятор CPM
- Калькулятор коэффициента долга
- Калькулятор скидки
- Калькулятор маржи
- GST Налоговый калькулятор
- Калькулятор прямой амортизации
- Калькулятор НДС
- Калькулятор ИМТ
- Калькулятор BMR
- Калькулятор даты зачатия
- Калькулятор даты родов
- Калькулятор дробей
- Упрощение дробей
- Калькулятор GCF
- ЖК-калькулятор
- Калькулятор LCM
- Калькулятор процентов
- Калькулятор округления чисел
- Квадратный корень Ca lculator
- Преобразование единиц
- Преобразование площади
- Преобразование длины
- Преобразование давления
- Преобразование температуры
- Преобразование времени
- Преобразование объема
- 9000 Преобразование веса
- в калькулятор дробей
- Калькулятор десятичных дробей в проценты
- Калькулятор дробей в десятичные
- Калькулятор дробей в проценты
- Калькулятор процентов в десятичные
- Калькулятор процентов в дроби
- Конвертер римских цифр
javascript — Расчет чистой приведенной стоимости
Переполнение стека- Около
- Продукты
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- Вакансии Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- Реклама Обратитесь к разработчикам и технологам со всего мира
- О компании
Рассчитайте чистую приведенную стоимость — NPV
Чистая приведенная стоимость (NPV) — это сумма приведенных стоимостей денег в различные будущие моменты времени.
Текущая стоимость (PV) определяет, сколько будущих денег стоят сегодня . Основываясь на чистой текущей стоимости, мы можем сравнить набор проектов / инвестиций с различными денежными потоками с течением времени. Это позволяет нам количественно оценить привлекательность бизнеса, используя сравнительный анализ NPV.
Чем ближе будущие денежные потоки к настоящему, тем ценнее ваши деньги
Концепция также известна как временная стоимость денег , и мы даем два объяснения ниже:
- Интуитивное объяснение : В настоящее время люди будут предпочитать деньги из-за неприятие риска .Вы бы предпочли иметь 100 долларов сегодня или через год? Очевидно, сегодня, потому что есть риск, что вы не получите эти 100 долларов в год. Кроме того, как только у вас появятся деньги, у вас снова будет решение либо потратить их сразу, либо подождать, чтобы потратить.
- A financial объяснение: Представьте, что у вас есть 100 долларов. Сколько это стоит в год? Если вы не оставляете деньги в кармане, у вас обычно есть возможность положить деньги на свой банковский счет с низким и почти незначительным риском.Вы будете получать проценты , но можете потерять ценность из-за инфляции. Однако процентная ставка с поправкой на инфляцию может составлять 2%, в абсолютном выражении 2 доллара. В общей сложности ваши 100 долларов будут стоить 102 доллара через год. Теперь вы можете рассчитать в обратном направлении: если ваша будущая стоимость составляет 102 доллара через год, сколько она стоит сегодня? 102 доллара делятся на 1,02, что снова дает 100 долларов.
Как рассчитать чистую приведенную стоимость
- PV — текущая стоимость
- FV — будущая стоимость
- i — десятичное значение процентной ставки за определенный период
- n — количество периодов между настоящим и будущим
Ниже приводится расчет приведенного выше примера PV с будущей стоимостью 102 доллара при процентной ставке 2%,
Ниже вы можете найти немного другую версию из приведенного выше примера, в которой вы получите 102 доллара за за два года вместо следующего года.
Двухлетние инвестиции приносят вам теоретический процент два раза, поэтому вы дважды дисконтируете.
Чистая приведенная стоимость этих двух платежей по 102 доллара через один и два года — это просто их сумма.
Применение сокращений NPV для достижения успеха в ситуациях
Маловероятно, что вам понадобится для расчета комплексной чистой приведенной стоимости во время интервью, потому что расчеты имеют тенденцию становиться слишком сложными.Но в некоторых случаях вы можете применить некоторые ярлыки, как описано ниже:
1) Бесконечность: NPV для бесконечных денежных потоков (то есть бизнес будет приносить прибыль в течение бесконечного периода времени)
Для бесконечных денежных потоков существует упрощенная формула:
Представьте, что вам нужно оценить компанию в в ходе собеседования. Общий подход состоит в том, чтобы определить стоимость компании как сумму всей ее дисконтированной будущей прибыли .
Если вы предполагаете, что компания будет получать одинаковую прибыль каждый год в течение неопределенного периода времени, вы просто разделите будущую стоимость всей прибыли на соответствующую ставку дисконтирования. Например, если вы ожидаете, что компания будет приносить 100 долларов в год, компания стоит 2500 долларов (при ставке дисконтирования 4%).
Чтобы сделать это более прагматичным, можно предположить, что прибыль компании будет расти каждый год с определенной скоростью g.
Особенно для краткосрочных горизонтов определить ожидаемый рост сложно.Приблизительный темп роста прибыли в далеком будущем часто составляет около 2% . Через некоторое время каждый жизненный цикл бизнеса или продукта заканчивается в конкурентной рыночной среде и просто растет с той же скоростью, что и экономика в целом . Приведенный выше пример, пересчитанный с постоянной скоростью роста 2%, дает чистую приведенную стоимость в размере 5000 долларов США.
Обратите внимание, что значение в два раза превышает значение по сравнению с расчетами без увеличения.Расчеты NPV очень чувствительны, , к изменениям входов. Поэтому в большинстве случаев проводится анализ чувствительности. Для этого вам необходимо создать диапазон возможных значений NPV, используя диапазон возможных темпов роста и дисконтирования.
2. Найдите подходящую процентную ставку i
Поиск правильного коэффициента дисконтирования для расчета NPV — дело целых банковских отделов. В общем, есть одно основное правило: чем больше риск, тем выше ставка дисконтирования.
Обоснование этого правила простое: чем меньше вы можете быть уверены в получении будущих доходов, тем меньше вы их цените. При увеличении ставки дисконтирования ЧПС будущих доходов уменьшится на на . Ставки дисконтирования для достаточно безопасных денежных потоков варьируются от 1% до 3%, но для большинства компаний вы используете ставку дисконтирования от 4% до 10%, а для спекулятивных стартовых инвестиций применяемая процентная ставка может достигать 40%.
%. В случае собеседований вы можете запросить ставку дисконтирования напрямую или оценить ее в 10% для большинства сценариев, если интервьюер попросит вас приблизить ее.
Основные выводы
- Используйте NPV для оценки будущих денежных потоков с учетом сегодняшней стоимости денег.
- Вычислив NPV с поправкой на риск, вы можете количественно сравнить различные инвестиции .
- NPV используются для оценки компании на основе ее будущей прибыли.
Ohne Dein Einverständnis können wir keine YouTube-Videos einbetten.Klicke auf den Button, um dem automatischen Einbetten von YouTube Videos zuzustimmen .
Mit Deiner Zustimmung willigst Du zugleich драгоценный камень. Изобразительное искусство. 49 Абс. 1 С. 1 лит. a DSGVO ein, dass Deine Daten in den USA verarbeitet werden.
Du kannst Dein Einverständnis jederzeit in unseren Cookie- und Privatsphäre-Einstellungen ändern.
Анализ чувствительности | Чистая приведенная стоимость (ЧПС) | Внутренняя норма доходности (IRR) | Бюджетирование капиталовложений | Пример
Юрий Смирнов к.Д.Определение
Анализ чувствительности используется для оценки того, насколько чувствительна выходная переменная к изменению одной из переменных, в то время как другие входные переменные остаются неизменными. Анализ чувствительности широко используется при принятии решений по капитальному бюджету для оценки того, как изменение таких входов, как продажи, переменные затраты, постоянные затраты, стоимость капитала и предельная ставка налога повлияет на такие результаты, как чистая приведенная стоимость (NPV) проекта, внутренняя норма доходности (IRR) и дисконтированный срок окупаемости.Это также обеспечивает лучшее понимание рисков, связанных с проектом.
Как проводить анализ чувствительности
Анализ чувствительности проекта включает несколько шагов.
- Определите входные и выходные переменные.
- Вычислить базовое значение выходной переменной, используя значение базовых входных переменных.
- Измените значение одной из входных переменных, пока другие остаются постоянными, и вычислите новое значение выходной переменной.
- Рассчитайте процентное изменение выходной и входной переменных по сравнению с базовыми значениями.
- Рассчитайте чувствительность выходной переменной к изменению входной переменной, используя формулу ниже.
Формула
| Чувствительность = | % изменение выпуска |
| % изменение на входе |
Шаги с третьего по пятый следует повторить для других входных переменных.
Анализ чувствительности позволяет идентифицировать входные переменные, которые представляют наибольшую уязвимость для проекта.
Пример
Компания рассматривает проект с первоначальной стоимостью $ 500 000, включающий покупку нового оборудования со сроком полезного использования 5 лет.
Стоимость капитала после уплаты налогов составляет 16%, а предельная ставка налога — 30%. Остальные ключевые параметры проекта представлены в таблице ниже.
Расходы на амортизацию в размере 40 000 долларов США в год включены в постоянные затраты.
Руководство компании проведет анализ чувствительности проекта.
Решение
Шаг 1
Руководство определяет чистую приведенную стоимость (NPV) и внутреннюю норму прибыли (IRR) в качестве результатов. Входы:
- Постоянные затраты
- Продажи в единицах
- Цена продажи за единицу
- Переменные затраты на единицу
Шаг 2
Давайте найдем базовые значения NPV и IRR.Расчет дисконтированных денежных потоков представлен в таблице ниже.
Расчет дисконтированного чистого денежного потока для назначенного года 1 показан ниже.
S = 20000 × 35 = 700000 долларов
TVC = 20 000 × 22 доллара = 440 000 долларов
EBT = 700 000 — 440 000 — 100 000 долларов = 160 000 долларов
T = 160 000 долларов США × 30% = 48 000 долларов США
NI = 160 000 — 48 000 долларов = 112 000 долларов
NCF = 112 000 долларов США + 40 000 долларов США = 152 000 долларов США
| DNCF = | 152 000 долл. США | = 131 034 долл. США |
| (1 + 0.16) 1 |
Дисконтированные чистые денежные потоки в другие определенные годы рассчитываются таким же образом.
Базовая чистая приведенная стоимость проекта составляет:
Базовая ЧПС = — 500 000 долларов США + 131 034 доллара США + 136 891 доллар США + 160 164 доллара США + 137 686 долларов США + 111 030 долларов США = 176 805 долларов США
Базовая IRR составляет 29,03%. Вы можете прочитать здесь, как рассчитать IRR в Excel.
Шаг 3
Предположим, постоянные затраты будут на 5% выше базовых значений.При условии, что прочие исходные данные останутся неизменными, дисконтированные чистые денежные потоки будут следующими:
NPV = — 500 000 долларов США + 128 017 долларов США + 134 238 долларов США + 157 810 долларов США + 135 579 долларов США + 109 113 долларов США = 164 757 долларов США
| % изменение NPV = | 164 757–176 805 долл. США | = -6,81% |
| 176 805 долл. США |
| Чувствительность NPV = | -6,81% | = -1.362 |
| 5% |
Это означает, что при увеличении постоянных затрат на 1% чистая приведенная стоимость проекта уменьшится на 1,362%, и наоборот, если постоянные затраты уменьшены на 1%, чистая приведенная стоимость увеличится на 1,362%.
Новое значение IRR составляет 28,17%
| % изменение IRR = | 28,17% -29,03% | = -2,96% |
| 29,03% |
| Чувствительность IRR = | -2.96% | = -0,592 |
| 5% |
Шаг 4
Предположим, что продажи в единицах будут на 5% выше базовых значений.
При условии, что прочие исходные данные останутся неизменными, дисконтированные чистые денежные потоки будут следующими:
Обратите внимание, что изменение количества проданных единиц влияет как на объем продаж, так и на общие переменные затраты!
NPV = — 500 000 долларов США + 138 879 долларов США + 144 902 доллара США + 169 246 долларов США + 145 573 долларов США + 117 545 долларов США = 216 145 долларов США
| % изменение NPV = | 216 145–176 805 долларов | = 22.25% |
| 176 805 долл. США |
| Чувствительность NPV = | 22,25% | = 4,450 |
| 5% |
Таким образом, увеличение продаж на 1% вызовет увеличение NPV на 4,450% и наоборот.
Новое значение IRR составляет 31,73%
| % изменение IRR = | 31.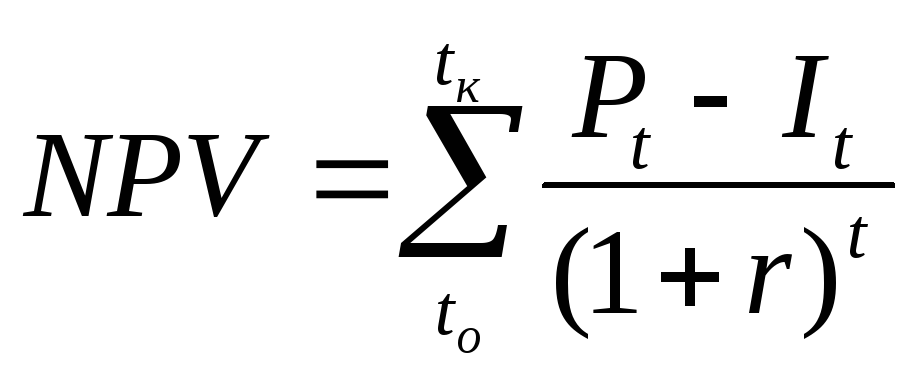 73% -29,03% | = 9,30% |
| 29,03% |
| Чувствительность IRR = | 9,30% | = 1,860 |
| 5% |
Шаг 5
Предположим, что продажная цена единицы будет на 5% выше базовых значений. При условии, что прочие исходные данные останутся неизменными, дисконтированные чистые денежные потоки будут следующими:
Обратите внимание, изменение продажной цены влияет только на показатели продаж!
NPV = — 500 000 долларов США + 152 155 долларов США + 157 491 доллар США + 183 170 долларов США + 157 896 долларов США + 128 277 долларов США = 278 989 долларов США
| % изменение NPV = | 278 989–176 805 долл. США | = 57.79% |
176 805 долл. США |
| Чувствительность NPV = | 57,79% | = 11,558 |
| 5% |
Увеличение продажной цены на 1% приведет к увеличению NPV на 11,558%, а если цена продажи упадет на 1%, NPV проекта уменьшится на 11,558%.
Новое значение IRR — 35.95%
| % изменение IRR = | 35,95% -29,03% | = 23,84% |
| 29,03% |
| Чувствительность IRR = | 9,30% | = 4,768 |
| 5% |
Шаг 6
Предположим, что переменные затраты на единицу продукции будут на 5% выше базовых значений.При условии, что прочие исходные данные останутся неизменными, дисконтированные чистые денежные потоки будут следующими:
NPV = — 500 000 долларов США + 117 759 долларов США + 124 301 доллар США + 146 240 долларов США + 125 363 долларов США + 100 298 долларов США = 113 961 долларов США
| % изменение NPV = | 113 961–176 805 долл. США | = -35,54% |
| 176 805 долл. США |
| Чувствительность NPV = | -35,54% | = -7.109 |
| 5% |
Увеличение переменных затрат на единицу на 1% приведет к снижению NPV на 7,109% и наоборот.
Новое значение IRR составляет 24,57%
| % изменение IRR = | 24,57% — 29,03% | = -15,36% |
| 29,03% |
| Чувствительность IRR = | -15.36% | = -3,072 |
| 5% |
Результаты анализа чувствительности
Анализ чувствительности показывает, что NPV и IRR проекта наиболее уязвимы к изменению продажной цены и переменных затрат на единицу и менее уязвимы к изменению постоянных затрат и продаж в единицах.
График
Результаты анализа чувствительности в приведенном выше примере показаны на графике ниже.
Как мы видим, руководство компании должно оценить продажную цену и переменные затраты как можно точнее, потому что они имеют наибольшее влияние на чистую приведенную стоимость проекта.
Если эта статья была для вас полезной, пожалуйста, поблагодарите наших авторов!
$ ПОДАРИТЬ
Приложение: Таблицы приведенной стоимости
Расчет текущей стоимости. Для каждого из следующих независимых сценариев используйте рисунок 8.9 «Текущая стоимость 1 доллара, полученного в конце» в приложении, чтобы рассчитать приведенную стоимость описанного денежного потока.
- 10 000 долларов будут получены через 4 года. Ставка составляет 10 процентов.
- 10 000 долларов будут получены через 4 года с сегодняшнего дня.Ставка составляет 20 процентов.
- 50 000 долларов будет получено через 15 лет. Ставка составляет 12 процентов.
- 50 000 долларов будет получено через 15 лет. Ставка составляет 6 процентов.
Расчет текущей стоимости (аннуитетов). Для каждого из следующих независимых сценариев используйте рисунок 8.10 «Текущая стоимость аннуитета в размере 1 доллара, полученного в конце каждого периода для» в приложении, чтобы рассчитать приведенную стоимость описанного денежного потока.Округлить до ближайшего доллара.
- 1000 долларов будут получать в конце каждого года в течение 6 лет. Ставка составляет 12 процентов.
- 1000 долларов будут получать в конце каждого года в течение 6 лет. Ставка составляет 15 процентов.
- 10 000 долларов будут получать в конце каждого года в течение 6 лет. Ставка составляет 7 процентов.
- 250 000 долларов будут получены в конце каждого года в течение 4 лет. Ставка составляет 10 процентов.
Ставка составляет 12 процентов.Расчеты чистой приведенной стоимости. У Freefall, Inc. есть две независимые инвестиционные возможности, каждая из которых требует первоначальных вложений в размере 65 000 долларов США. Требуемая норма прибыли компании составляет 8 процентов. Приток денежных средств по каждой инвестиции представлен следующим образом.
Требуется:
- Какие инвестиции будут иметь наибольшую чистую приведенную стоимость, не прибегая к расчетам? Объясни.
- Рассчитайте чистую приведенную стоимость для каждой инвестиции (не забудьте включить в свои расчеты первоначальный отток денежных средств по инвестициям). Следует ли компании инвестировать в любую из инвестиций? Округлить до ближайшего доллара.
Этические вопросы при принятии решения о капитальном бюджете.
Предположим, что менеджер магазина получает годовой бонус, основанный на достижении определенного уровня чистой прибыли, стабильно полученной в течение последних пяти лет. В настоящее время компания рассматривает возможность открытия второго магазина, который, как ожидается, станет прибыльным через два года. Менеджер несет ответственность за принятие окончательного решения о том, следует ли открывать второй магазин, и получит годовой бонус только в том случае, если для обоих магазинов вместе взятых будет достигнут определенный уровень чистой прибыли.
Почему менеджер может отказаться вкладывать средства в новый магазин, даже если предполагается, что инвестиции принесут прибыль, превышающую требуемую для компании норму прибыли?
Требуемая норма прибыли компании составляет 11 процентов. Используйте Excel, чтобы рассчитать чистую приведенную стоимость этих инвестиций в формате, аналогичном формату, указанному в поле Computer Application в этой главе.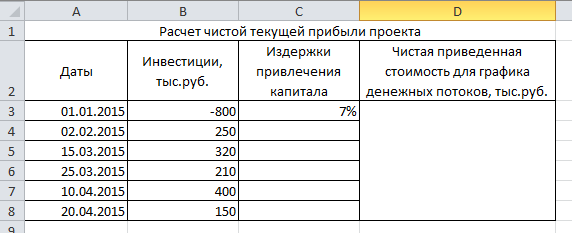
Инвестиция, стоимость которой сегодня составляет 200 000 долларов, приведет к экономии денежных средств в размере 85 000 долларов в год в течение 3 лет. У компании ставка налога составляет 40 процентов, а норма прибыли — 11 процентов. Найдите чистую приведенную стоимость этих инвестиций, используя формат, показанный на Рисунке 8.7 «Расчет NPV с налогами на прибыль для Scientific Products, Inc.». Округлить до ближайшего доллара.Анализ чистой приведенной стоимости. Architect Services, Inc., хотела бы приобрести машину для чертежей за 50 000 долларов. Ожидается, что срок службы машины составит 4 года, а аварийная стоимость — 10 000 долларов. Ежегодные расходы на техническое обслуживание составят 14 000 долларов. Ожидается, что годовая экономия составит 30 000 долларов. Требуемая норма прибыли компании составляет 11 процентов.
Требуется:
- Игнорируя временную стоимость денег, рассчитайте чистый приток или отток денежных средств в результате этой инвестиционной возможности.
- Найдите чистую приведенную стоимость этих инвестиций, используя формат, представленный на Рисунке 8.2 «Расчет NPV для инвестиций в копировальный аппарат с помощью качественных копий Джексона».
- Следует ли компании покупать чертежную машину? Объясни.
Анализ внутренней нормы прибыли. Architect Services, Inc., хотела бы приобрести машину для чертежей за 50 000 долларов.Ожидается, что срок службы машины составит 4 года, а аварийная стоимость — 10 000 долларов. Ежегодные расходы на техническое обслуживание составят 14 000 долларов. Ожидается, что годовая экономия составит 30 000 долларов. Требуемая норма прибыли компании составляет 11 процентов (это те же данные, что и в предыдущем упражнении).
Требуется:
- Используйте метод проб и ошибок, чтобы приблизительно определить внутреннюю норму прибыли для этого инвестиционного предложения. Округлить до ближайшего доллара.
- Следует ли компании покупать чертежную машину? Объясни.
Округлить до ближайшего доллара. Анализ чистой приведенной стоимости с несколькими инвестициями, альтернативный формат. Conway Construction Corporation хотела бы приобрести парк грузовых автомобилей по цене 260 000 долларов. Дополнительное оборудование, необходимое для обслуживания парка грузовиков, будет закуплено в конце второго года за 40 000 долларов.
Ожидается, что срок службы грузовиков составит 8 лет, а аварийная стоимость — 20 000 долларов. Годовые затраты на обслуживание, страхование и другие денежные расходы составят 42 000 долларов.Ожидается, что годовые чистые денежные поступления от этой покупки составят 135 000 долларов. Требуемая норма прибыли компании составляет 14 процентов.
Требуется:
- Найдите чистую приведенную стоимость этих инвестиций, используя формат, представленный на Рисунке 8.4 «Альтернативный расчет NPV для качественных копий Джексона».
- Стоит ли компании приобретать новый парк грузовых автомобилей? Объясни.
Расчет NPV и IRR с помощью Excel. Wood Products Company хотела бы приобрести компьютеризированный токарный станок по дереву за 100 000 долларов. Ожидается, что срок службы машины составит 5 лет, а аварийная стоимость — 5 000 долларов.
Ежегодные расходы на техническое обслуживание составят 20 000 долларов. Ожидается, что годовые чистые денежные поступления от этой машины составят 45 000 долларов. Требуемая норма прибыли компании составляет 15 процентов.
Требуется:
- Используйте Excel для расчета чистой приведенной стоимости и внутренней нормы прибыли в формате, аналогичном электронной таблице Computer Application , показанной в этой главе.
- Стоит ли компании покупать токарный станок по дереву? Объясни.
Анализ чистой приведенной стоимости с налогами. Компания Timberline желает приобрести новую машину за 100 000 долларов. Срок службы машины составит 5 лет без стоимости утилизации, и ожидается, что она будет приносить денежный доход в размере 50 000 долларов в год. Ежегодные денежные расходы без учета амортизации составят 24 000 долларов.
Компания использует линейный метод начисления амортизации, имеет ставку налога 40 процентов и требует 12-процентной нормы прибыли.
Требуется:
Расчет чистой приведенной стоимости
Чистая приведенная стоимость (NPV) является наиболее важным понятием в корпоративных финансах. Именно на основе этой концепции принимаются или не принимаются инвестиционные решения. Именно на основе этой концепции оцениваются акции и облигации. Таким образом, абсолютно необходимо, чтобы каждый студент, изучающий корпоративные финансы, досконально разбирался в этой концепции. Чтобы понять концепцию чистой приведенной стоимости, необходимо иметь четкое представление о расчетах будущей и приведенной стоимости.ЧДД лучше всего понять с помощью графика движения денежных средств. В этой статье будет использоваться то же самое, чтобы объяснить это:
График движения денежных средств:
График движения денежных средств представляет собой периоды, когда ожидается, что денежные средства будут выплачены или получены в ходе проекта.
Point Zero, представляет сегодня. Следовательно, все суммы, указанные в нулевой точке, являются текущими значениями. Нам не нужно корректировать их путем сложения или дисконтирования для расчета чистой приведенной стоимости.
Значения, перечисленные в пункте 1, представляют собой суммы, которые будут получены или выплачены в конце первого периода.Значения, указанные в периоде 2, представляют собой суммы, которые будут получены или выплачены в конце периода 2 и т. Д., И т. Д.
Будущие значения возникают в разные периоды
Когда мы сравниваем два числа, мы должны убедиться, что они имеют схожий характер. Следовательно, при сравнении денежных потоков мы должны убедиться, что все они представляют собой текущую стоимость или будущую стоимость, принадлежащую одному и тому же будущему периоду. Сравнение текущей стоимости с будущей стоимостью или сравнение будущей стоимости в периоде 1 с будущей стоимостью в периоде 2 похоже на сравнение яблок с апельсинами.
Поскольку все будущие ценности происходят в разные периоды, мы не можем сравнивать их друг с другом.
Единственный способ сложить или вычесть эти значения — это вернуть их все к нулевому дню, то есть преобразовать каждое будущее значение в их эквивалентные текущие значения.
Текущие значения появляются в одно и то же время, т.е. нулевой день
Поскольку текущая стоимость отражает стоимость денег в нулевой день, то есть в тот же период, было бы правильным сложить, вычесть или выполнить любую другую математическую операцию с этим числом.Ключевым моментом для понимания является то, что все значения, участвующие в расчетах, должны быть текущими значениями.
Пример расчета NPV
Рассмотрим следующий график оттока и поступления денежных средств:
Период 0: Отток денежных средств в размере 10 000 долларов
Период 1: приток $ 5 000
Период 2: приток $ 4,000
Период 3: приток $ 3,500
Период 4: приток $ 3,000
Стоимость капитала 10%.
Вопрос в том, разумно ли с финансовой точки зрения инвестировать сегодня 10 000 долларов и получать 4 взноса по 5000, 4000, 3500 и 3000 долларов, если наша стоимость капитала составляет 10%.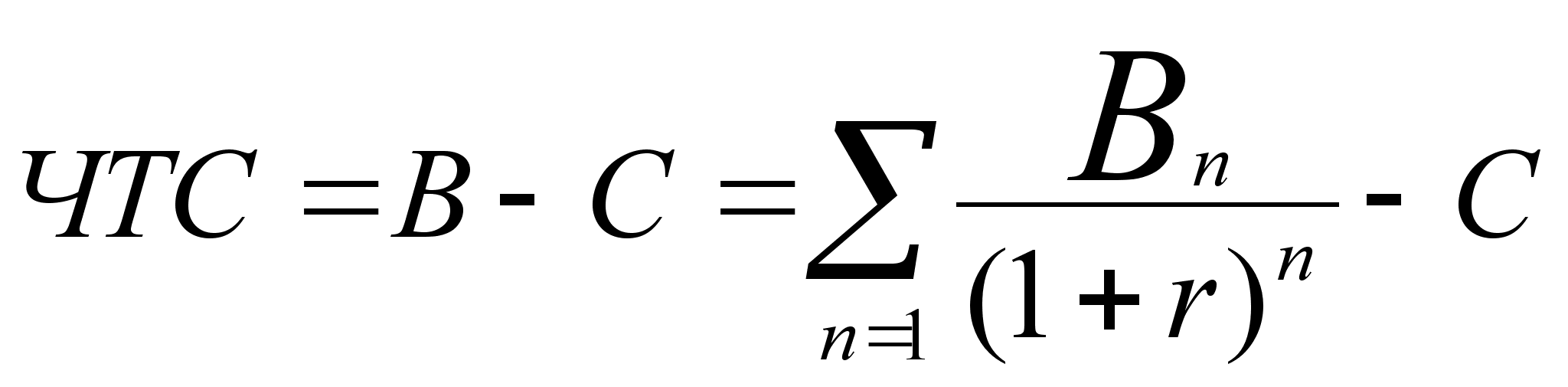
Раствор:
Отток: 10 000 долл. США
Текущая стоимость притока: PV (приток в год 1) + PV (приток в год 2) + PV (приток в год 3) + PV (приток в год 4)
= (5000 долларов / 1,1) 1 + (4000 долларов / 1,1) 2 + (3500 долларов / 1,1) 3 + (3000 долларов / 1,1) 4
= 4545,46 долл. США + 3305,79 долл. США + 2 629,60 долл. США + 2049,04 долл. США
= 12 529,89 долл. США
Чистая приведенная стоимость = приведенная стоимость притока — приведенная стоимость оттока
= 12 529–10 000 долларов
= 2 529 долл. США
Правило о чистой приведенной стоимости
Правило чистой приведенной стоимости гласит, что если ЧПС предложения больше 0, оно должно быть принято.При меньшем или равном нулю предложения должны быть отклонены. В этом случае NPV составляет 2529 долларов. Следовательно, это предложение является финансово обоснованным с учетом стоимости капитала фирмы.