Как посчитать коэффициент вариации в excel
Расчет коэффициента вариации в Microsoft Excel
Одним из основных статистических показателей последовательности чисел является коэффициент вариации. Для его нахождения производятся довольно сложные расчеты. Инструменты Microsoft Excel позволяют значительно облегчить их для пользователя.
Вычисление коэффициента вариации
Этот показатель представляет собой отношение стандартного отклонения к среднему арифметическому. Полученный результат выражается в процентах.
В Экселе не существует отдельно функции для вычисления этого показателя, но имеются формулы для расчета стандартного отклонения и среднего арифметического ряда чисел, а именно они используются для нахождения коэффициента вариации.
Шаг 1: расчет стандартного отклонения
Стандартное отклонение, или, как его называют по-другому, среднеквадратичное отклонение, представляет собой квадратный корень из дисперсии. Для расчета стандартного отклонения используется функция СТАНДОТКЛОН. Начиная с версии Excel 2010 она разделена, в зависимости от того, по генеральной совокупности происходит вычисление или по выборке, на два отдельных варианта: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В.
Начиная с версии Excel 2010 она разделена, в зависимости от того, по генеральной совокупности происходит вычисление или по выборке, на два отдельных варианта: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В.
Синтаксис данных функций выглядит соответствующим образом:
= СТАНДОТКЛОН(Число1;Число2;…)
= СТАНДОТКЛОН.Г(Число1;Число2;…)
= СТАНДОТКЛОН.В(Число1;Число2;…)
- Для того, чтобы рассчитать стандартное отклонение, выделяем любую свободную ячейку на листе, которая удобна вам для того, чтобы выводить в неё результаты расчетов. Щелкаем по кнопке «Вставить функцию». Она имеет внешний вид пиктограммы и расположена слева от строки формул.
Шаг 2: расчет среднего арифметического
Среднее арифметическое является отношением общей суммы всех значений числового ряда к их количеству. Для расчета этого показателя тоже существует отдельная функция – СРЗНАЧ. Вычислим её значение на конкретном примере.
- Выделяем на листе ячейку для вывода результата.
 Жмем на уже знакомую нам кнопку «Вставить функцию».
Жмем на уже знакомую нам кнопку «Вставить функцию».Шаг 3: нахождение коэффициента вариации
Теперь у нас имеются все необходимые данные для того, чтобы непосредственно рассчитать сам коэффициент вариации.
- Выделяем ячейку, в которую будет выводиться результат. Прежде всего, нужно учесть, что коэффициент вариации является процентным значением. В связи с этим следует поменять формат ячейки на соответствующий. Это можно сделать после её выделения, находясь во вкладке «Главная». Кликаем по полю формата на ленте в блоке инструментов «Число». Из раскрывшегося списка вариантов выбираем «Процентный». После этих действий формат у элемента будет соответствующий.
Таким образом мы произвели вычисление коэффициента вариации, ссылаясь на ячейки, в которых уже были рассчитаны стандартное отклонение и среднее арифметическое. Но можно поступить и несколько по-иному, не рассчитывая отдельно данные значения.
- Выделяем предварительно отформатированную под процентный формат ячейку, в которой будет выведен результат. Прописываем в ней формулу по типу:
Существует условное разграничение. Считается, что если показатель коэффициента вариации менее 33%, то совокупность чисел однородная. В обратном случае её принято характеризовать, как неоднородную.
Как видим, программа Эксель позволяет значительно упростить расчет такого сложного статистического вычисления, как поиск коэффициента вариации. К сожалению, в приложении пока не существует функции, которая высчитывала бы этот показатель в одно действие, но при помощи операторов СТАНДОТКЛОН и СРЗНАЧ эта задача очень упрощается. Таким образом, в Excel её может выполнить даже человек, который не имеет высокого уровня знаний связанных со статистическими закономерностями.
Мы рады, что смогли помочь Вам в решении проблемы.
Помимо этой статьи, на сайте еще 12345 инструкций.
Добавьте сайт Lumpics. ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Прогнозируем с Excel: как посчитать коэффициент вариации
Каждый раз, выполняя в Excel статистический анализ, нам приходится сталкиваться с расчётом таких значений, как дисперсия, среднеквадратичное отклонение и, разумеется, коэффициент вариации. Именно расчёту последнего стоит уделить особое внимание. Очень важно, чтобы каждый новичок, который только приступает к работе с табличным редактором, мог быстро подсчитать относительную границу разброса значений.
В этой статье мы расскажем, как автоматизировать расчеты при прогнозировании данных
Что такое коэффициент вариации и для чего он нужен?
Итак, как мне кажется, нелишним будет провести небольшой теоретический экскурс и разобраться в природе коэффициента вариации. Этот показатель необходим для отражения диапазона данных относительно среднего значения. Иными словами, он показывает отношение стандартного отклонения к среднему значению. Коэффициент вариации принято измерять в процентном выражении и отображать с его помощью однородность временного ряда.
Иными словами, он показывает отношение стандартного отклонения к среднему значению. Коэффициент вариации принято измерять в процентном выражении и отображать с его помощью однородность временного ряда.
Коэффициент вариации станет незаменимым помощником в том случае, когда вам необходимо будет сделать прогноз по данным из заданной выборки. Этот индикатор выделит главные ряды значений, которые будут наиболее полезными для последующего прогнозирования, а также очистит выборку от малозначительных факторов. Так, если вы видите, что значение коэффициента равно 0%, то с уверенностью заявляйте о том, что ряд является однородным, а значит, все значения в нём равны один с другим. В случае, если коэффициент вариации принимает значение, превышающее отметку в 33%, то это говорит о том, что вы имеете дело с неоднородным рядом, в котором отдельные значения существенно отличаются от среднего показателя выборки.
Как найти среднее квадратичное отклонение?
Поскольку для расчёта показателя вариации в Excel нам необходимо использовать среднее квадратичное отклонение, то вполне уместно будет выяснить, как нам посчитать этот параметр.
Из школьного курса алгебры мы знаем, что среднее квадратичное отклонение — это извлечённый из дисперсии квадратный корень, то есть этот показатель определяет степень отклонения конкретного показателя общей выборки от её среднего значения. С его помощью мы можем измерить абсолютную меру колебания изучаемого признака и чётко её интерпретировать.
Рассчитываем коэффициент в Экселе
К сожалению, в Excel не заложена стандартная формула, которая бы позволила рассчитать показатель вариации автоматически. Но это не значит, что вам придётся производить расчёты в уме. Отсутствие шаблона в «Строке формул» никоим образом не умаляет способностей Excel, потому вы вполне сможете заставить программу выполнить необходимый вам расчёт, прописав соответствующую команду вручную.
Вставьте формулу и укажите диапазон данных
Для того чтобы рассчитать показатель вариации в Excel, необходимо вспомнить школьный курс математики и разделить стандартное отклонение на среднее значение выборки. То есть на деле формула выглядит следующим образом — СТАНДОТКЛОН(заданный диапазон данных)/СРЗНАЧ(заданный диапазон данных). Ввести эту формулу необходимо в ту ячейку Excel, в которой вы хотите получить нужный вам расчёт.
То есть на деле формула выглядит следующим образом — СТАНДОТКЛОН(заданный диапазон данных)/СРЗНАЧ(заданный диапазон данных). Ввести эту формулу необходимо в ту ячейку Excel, в которой вы хотите получить нужный вам расчёт.
Не забывайте и о том, что поскольку коэффициент выражается в процентах, то ячейке с формулой нужно будет задать соответствующий формат. Сделать это можно следующим образом:
- Откройте вкладку «Главная».
- Найдите в ней категорию «Формат ячеек» и выберите необходимый параметр.
Как вариант, можно задать процентный формат ячейке при помощи клика по правой кнопке мыши на активированной клеточке таблицы. В появившемся контекстном меню, аналогично вышеуказанному алгоритму нужно выбрать категорию «Формат ячейки» и задать необходимое значение.
Выберите «Процентный», а при необходимости укажите число десятичных знаков
Возможно, кому-то вышеописанный алгоритм покажется сложным. На самом же деле расчёт коэффициента так же прост, как сложение двух натуральных чисел. Единожды выполнив эту задачу в Экселе, вы больше никогда не вернётесь к утомительным многосложным решениям в тетрадке.
Единожды выполнив эту задачу в Экселе, вы больше никогда не вернётесь к утомительным многосложным решениям в тетрадке.
Всё ещё не можете сделать качественное сравнение степени разброса данных? Теряетесь в масштабах выборки? Тогда прямо сейчас принимайтесь за дело и осваивайте на практике весь теоретический материал, который был изложен выше! Пусть статистический анализ и разработка прогноза больше не вызывают у вас страха и негатива. Экономьте свои силы и время вместе с табличным редактором Excel.
Коэффициент вариации: формула и расчет в Excel и интерпретация результатов
Коэффициент вариации в статистике применяется для сравнения разброса двух случайных величин с разными единицами измерения относительно ожидаемого значения. В итоге можно получить сопоставимые результаты. Показатель наглядно иллюстрирует однородность временного ряда.
Коэффициент вариации используется также инвесторами при портфельном анализе в качестве количественного показателя риска, связанного с вложением средств в определенные активы. Особенно эффективен в ситуации, когда у активов разная доходность и различный уровень риска. К примеру, у одного актива высокая ожидаемая доходность, а у другого – низкий уровень риска.
Особенно эффективен в ситуации, когда у активов разная доходность и различный уровень риска. К примеру, у одного актива высокая ожидаемая доходность, а у другого – низкий уровень риска.
Как рассчитать коэффициент вариации в Excel
Коэффициент вариации представляет собой отношение среднеквадратического отклонения к среднему арифметическому. Для расчета в статистике используется следующая формула:
- CV – коэффициент вариации;
- σ – среднеквадратическое отклонение по выборке;
- ǩ – среднеарифметическое значение разброса значений.
Коэффициент вариации позволяет сравнить риск инвестирования и доходность двух и более портфелей активов. Причем последние могут существенно отличаться. То есть показатель увязывает риск и доходность. Позволяет оценить отношение между среднеквадратическим отклонением и ожидаемой доходностью в относительном выражении. Соответственно, сопоставить полученные результаты.
При принятии инвестиционного решения необходимо учитывать следующий момент: когда ожидаемая доходность актива близка к 0, коэффициент вариации может получиться большим. Причем показатель значительно меняется при незначительном изменении доходности.
Причем показатель значительно меняется при незначительном изменении доходности.
В Excel не существует встроенной функции для расчета коэффициента вариации. Но можно найти частное от стандартного отклонения и среднего арифметического значения. Рассмотрим на примере.
Доходность двух ценных бумаг за предыдущие пять лет:
Наглядно это можно продемонстрировать на графике:
Обычно показатель выражается в процентах. Поэтому для ячеек с результатами установлен процентный формат.
Значение коэффициента для компании А – 33%, что свидетельствует об относительной однородности ряда. Формула расчета коэффициента вариации в Excel:
Сравните: для компании В коэффициент вариации составил 50%: ряд не является однородным, данные значительно разбросаны относительно среднего значения.
Интерпретация результатов
Прежде чем включить в инвестиционный портфель дополнительный актив, финансовый аналитик должен обосновать свое решение. Один из способов – расчет коэффициента вариации.
Ожидаемая доходность ценных бумаг составит:
Среднеквадратическое отклонение доходности для активов компании А и В составляет:
Ценные бумаги компании В имеют более высокую ожидаемую доходность. Они превышают ожидаемую доходность компании А в 1,14 раза. Но и инвестировать в активы предприятия В рискованнее. Риск выше в 1,7 раза. Как сопоставить акции с разной ожидаемой доходностью и различным уровнем риска?
Для сопоставления активов двух компаний рассчитан коэффициент вариации доходности. Показатель для предприятия В – 50%, для предприятия А – 33%. Риск инвестирования в ценные бумаги фирмы В выше в 1,54 раза (50% / 33%). Это означает, что акции компании А имеют лучшее соотношение риск / доходность. Следовательно, предпочтительнее вложить средства именно в них.
Таким образом, коэффициент вариации показывает уровень риска, что может оказаться полезным при включении нового актива в портфель. Показатель позволяет сопоставить ожидаемую доходность и риск. То есть величины с разными единицами измерения.
То есть величины с разными единицами измерения.
Коэффициент вариации – что это, что показывает, формула расчета в Excel, среднеквадратичное и стандартное отклонение
Коэффициент вариации – это сравнение рассеивания двух случайно взятых величин. Величины имеют единицы измерения, что приводит к получению сопоставимого результата. Этот коэффициент нужен для подготовки статистического анализа.
С помощью него инвесторы могут рассчитать показатели риска перед тем, как сделать вклады в выбранные активы. Он полезен, когда у выбранных активов различная доходность и степень риска. К примеру, у одного актива может быть высокий доход и степень риска тоже высокая, а у другого, наоборот, малый доход и степень риска соответственно меньшая.
Расчет стандартного отклонения
Стандартное отклонение является статистической величиной. С помощью расчета этой величины пользователь получит информацию о том, насколько отклоняются данные в ту или иную сторону относительно среднего значения. Стандартное отклонение в Excel рассчитывается в несколько шагов.
Стандартное отклонение в Excel рассчитывается в несколько шагов.
Подготавливаете данные: открываете страницу, где будут происходить расчеты. В нашем случае это картинка, но может быть любой другой файл. Главное собрать ту информацию, которую будете использовать в таблице для рассчета.
Вводите данные в любой табличный редактор (в нашем случае Excel), заполняя ячейки слева направо. Начинать следует с колонки «А». Заголовки вводите в строке сверху, а названия в тех же столбцах, которые относятся к заголовкам, только ниже. Затем дату и данные, которые подлежат расчету, справа от даты.
Этот документ сохраняете.
Теперь переходим к самому вычислению. Выделяете курсором ячейку после последнего введенного значения снизу.
Вписываете знак «=» и прописываете далее формулу. Знак равенства обязателен. Иначе программа не посчитает предложенные данные. Формула вводится без пробелов.
Утилита выдаст названия нескольких формул.![]() Выбираете «СТАНДОТКЛОН». Это формула вычисления стандартного отклонения. Существует два вида расчета:
Выбираете «СТАНДОТКЛОН». Это формула вычисления стандартного отклонения. Существует два вида расчета:
- с вычислением по выборке;
- с вычислением по генеральной совокупности.
Выбрав одну из них, указываете диапазон данных. Вся введенная формула будет выглядеть так: «=СТАНДОТКЛОН (В2: В5)».
Затем кликаете по кнопке «Enter». Полученные данные появятся в отмеченном пункте.
Расчет среднего арифметического
Вычисляется, когда пользователю необходимо создать отчет, например, по заработной плате в его компании. Делается это следующим образом:
- открываете утилиту. В верхней строке набираете ряд нужных цифр;
- под первой цифрой ставите курсор. В верхней строке программы выбираете вкладку «Редактирование», затем кнопку «Сумма». В выпавшем окне выбираете значение «Среднее»;
- после того, как кликните в том пункте на котором стоит курсор, появится формула;
- останется только выделить диапазон и кликнуть по кнопке «Ввод».
 А в ячейке теперь отобразится результат из взятых данных выше.
А в ячейке теперь отобразится результат из взятых данных выше.
Расчет коэффициента вариации
Формула расчета коэффициента вариации:
V= S/X, где S – это стандартное отклонение, а X – среднее значение.
Для того, чтобы посчитать коэффициент вариации в Excel, необходимо найти стандартное отклонение и среднее арифметическое. То есть проделав первые два расчета, которые были показаны выше, можно перейти к работе над коэффициентом вариации.
Для этого открываете Excel, заполняем два поля, куда следует вписать полученные числа стандартного отклонения и среднего значения.
Теперь выделяете ячейку, которую отвели под число для вычисления вариации. Открываете вкладку «Главная», если она не открыта. Кликаете по инструменту «Число». Выбираете процентный формат.
Переходите к отмеченной ячейке и кликаете по ней дважды. Затем вводите знак равенства и выделяете пункт, куда вписан итог стандартного отклонения. Затем кликаете на клавиатуре по кнопке «слэш» или «разделить» (выглядит так: «/»). Выделяете пункт, куда вписано среднее арифметическое, и кликаете по кнопке «Enter». Должно получиться так:
Выделяете пункт, куда вписано среднее арифметическое, и кликаете по кнопке «Enter». Должно получиться так:
А вот и результат после нажатия «Enter»:
Также для расчета коэффициента вариации можно использовать онлайн калькуляторы, например planetcalc.ru и allcalc.ru. Достаточно внести необходимые цифры и запустить расчет, после чего получить необходимые сведения.
Среднеквадратическое отклонение
Среднеквадратичное отклонение в Excel решается с помощью двух формул:
Простыми словами, извлекается корень из дисперсии. Как вычислить дисперсию рассмотрено ниже.
Среднее квадратичное отклонение является синонимом стандартного и вычисляется точное также. Выделяется ячейка для результата под числами, которые нужно рассчитать. Вставляется одна из функций, указанных на рисунке выше. Кликается кнопка «Enter». Результат получен.
Коэффициент осциляции
Соотношением размаха вариации к среднему – называется коэффициентом осциляции. Готовых формул в Экселе нет, поэтому нужно компоновать несколько функций в одну.
Готовых формул в Экселе нет, поэтому нужно компоновать несколько функций в одну.
Функциями, которые необходимо скомпоновать, являются формулы среднего значения, максимума и минимума. Этот коэффициент используют для сравнения набора данных.
Дисперсия
Дисперсия – это функция, с помощью которой характеризуют разброс данных вокруг математического ожидания. Вычисляется по следующему уравнению:
Переменные принимают такие значения:
- Дисп.Г – используется относительно небольших выборок.
- Дисп.В – вычисление несмещенной дисперсии.
Чтобы произвести расчет, под числами, которые необходимо посчитать, выделяется ячейка. Заходите во вкладку вставки функции. Выбираете категорию «Статистические». В выпавшем списке выбираете одну из функций и кликаете по кнопке «Enter».
Максимум и минимум
Максимум и минимум нужны для того, чтобы не искать вручную среди большого количества чисел минимальное или максимальное число.
Чтобы вычислить максимум, выделяете весь диапазон необходимых чисел в таблице и отдельную ячейку, затем кликаете по значку «Σ» или «Автосумма». В выпавшем окне выбираете «Максимум» и, нажав кнопку «Enter» получаете нужное значение.
Тоже самое делаете, чтобы получить минимум. Только выбираете функцию «Минимум».
Концентрация, дифференциация и подобность распределения
Цель работы – освоить приемы анализу концентрации, дифференциации и подобности статистических распределений с помощью MS Excel.
Задание – провести анализ концентрации. Дифференциации и подобности статистических распределений, получить результативные показатели и объяснить полученные результаты.
Внизу приведены основные формулы показателей концентрации, дифференциации и подобности статистических распределений.
|
Коэффициент децильной дифференциации | |
|
Коэффициент локализации | |
|
Коэффициент концентрации | |
|
Линейный коэффициент структурних сдвигов | |
|
Коэффициент подобности структур |
Для решения задания 1 и 2 важно распознать суть абсолютных и относительных показателей, показателей локализации, концентрации и структурных сдвигов.
Задание 1
|
Размер заработной платы. |
Количество работающих, fi |
|
500-700 |
4 |
|
700-900 |
5 |
|
900-1100 |
17 |
|
1100-1300 |
20 |
|
1300-1500 |
25 |
| 1500-1700 |
14 |
|
1700-1900 |
9 |
|
1900 и больше |
7 |
Необходимо рассчитать показатели дифференциации размера заработной платы работающих.
Для расчета коэффициента дифференциации в MS Excel вводим данные в таком виде:
Для того чтобы рассчитать квартильный коэффициент вариации необходимо найти человек и медиану:
50 человек отвечают накопленной частоте интервала 1300-1500 грн. То есть этот интервал является медианным. Для того
Если данные представлены как не сгруппированный ряд распределения, то медиану можно рассчитать, используя стандартную функцию в Excel – МЕДИАНА.
Рассчитаем первый квартиль:
Используем формулу =B4+B11*(D10/4-E3)/D4
Рассчитаем третий квартиль. Используем следующую формулу =B7+B12*(D10*3/4-E6)/D7
Если данные представлены, как как не сгруппированный ряд распределения, то квартиль можно вычислить, используя стандартную функцию в Excel – КВАРТИЛЬ.
Для того чтобы рассчитать квартильный коэффициент вариации используем формулу =(B15-B14)/(2*B13)
Рассчитаем коэффициент децильной дифференциации. Для этого нам нужно рассчитать первый и девятый дециль.
Рассчитаем первый дециль с помощью формулы =B3+B14*(D10/10-E2)/D3
Теперь рассчитаем девятый дециль по формуле =B8+B15*(D10*9/10-E7)/D8
Теперь у нас есть все нужные данные, чтобы рассчитать коэффициент децильной дифференциации. Используем формулу =B18/B17
Соответственно минимальная заработная плата 10 % работников с максимально заработной платой в 1,47 раз больше максимальной заработной платы 10 % работников с минимальной заработной платой.
Задание 2
В таблице представлены данные про распределения предприятий и объема прибыли по отраслям экономики. С помощью коэффициентов локализации и концентрации нужно определить в какой отрасли вы бы разместили свое предприятие.
|
Отрасль |
2011 |
2012 | |
|
Кол-во объектов ЕГРПОУ |
Объем прибыли |
Объем прибыли | |
|
Всего |
1070705 |
3485,8 |
4204,9 |
| Сельское хозяйство, охота и лесное хозяйство |
85824 |
252,2 |
277,10291 |
|
Рыбное хозяйство |
1565 |
4 |
5,46637 |
|
Промышленность |
116260 |
1086,5 |
1426,30208 |
|
Строительство |
69866 |
124,3 |
92,5078 |
|
Оптовая и розничная торговля, торговля транспортными средствами, услуги по ремонту |
278097 |
330,6 |
317,89044 |
|
Отели и рестораны |
20264 |
30,4 |
54,6637 |
|
Транспорт и связь |
32497 |
289,6 |
374,2361 |
|
Финансовая деятельность |
15733 |
118 |
180,8107 |
|
Операция с недвижимостью, сдача в аренду и услуги юридическим лицам |
115249 |
151,6 |
260,7038 |
|
Государственное управление |
37145 |
213,5 |
238,83832 |
|
Образование |
38672 |
409,6 |
527,29446 |
|
Охрана здоровья и социальная помощь |
26007 |
372,6 |
402,82942 |
|
Коллективные, общественные и личные услуги |
131889 |
102,9 |
46,2539 |
|
Другое |
101637 |
0 |
0 |
Рассчитаем коэффициенты локализации, концентрации и объема прибыли на предприятиях разных отраслей и оценим интенсивность структурных сдвигов объема прибыли по отраслям экономики.
Для расчета показателей концентрации и подобности распределений в Excel на листе 2 вводим выходные данные.
Для дальнейших расчётов на листе 3 построим таблицу, в которой отображено доли предприятий и доли прибыли по предприятиям. Для этого в ячейке B3 вводим формулу =Лист2!B4/Лист2!$B$3*100. Потом растягиваем эту формулу на весь столбец. В ячейке С3 вводим формулу =Лист2!C4/Лист2!$C$3*100, в ячейки D3 вводим формулу =Лист2!D4/Лист2!$D$3*100, аналогично растягиваем эти формулы на весь столбец.
В итоге получаем такую таблицу.
Для расчета коэффициентов локализации в ячейке Е3 вводим формулу =C3/B3, потом растягиваем введенную формулу на весь столбец.
Рассчитываем коэффициент концентрации: в ячейку F3 вводим формулу =ABS(C3-B3) и растягиваем на весь столбец. В ячейке F18 рассчитываем сумму по столбцу.
Оценку структурных сдвигов и их интенсивность можно прочитать с помощью линейного коэффициента структурных сдвигов: в ячейке G3 вводим формулу =ABS(D3-C3). В ячейке G19 вводим формулу =СРЗНАЧ(G3:G16).
В ячейке G19 вводим формулу =СРЗНАЧ(G3:G16).
Получаем следующую таблицу:
Линейный коэффициент структурных сдвигов показал, что структура предприятия по объему прибыли в 2012 году по сравнению с 2011 годом изменилась незначительно, приблизительно на 1,48 процентов.
0
Коэффициент концентрации | Описание курса | Анализ динамики статистических показателей
Расчет дисперсии, среднеквадратичного (стандартного) отклонения, коэффициента вариации в Excel. Что такое стандартное отклонение — использование функции стандотклон для расчета стандартного отклонения в excel
Для того чтобы найти среднее значение в Excel (при том неважно числовое, текстовое, процентное или другое значение) существует много функций. И каждая из них обладает своими особенностями и преимуществами. Ведь в данной задаче могут быть поставлены определенные условия.
Например, средние значения ряда чисел в Excel считают с помощью статистических функций. Можно также вручную ввести собственную формулу. Рассмотрим различные варианты.
Можно также вручную ввести собственную формулу. Рассмотрим различные варианты.
Как найти среднее арифметическое чисел?
Чтобы найти среднее арифметическое, необходимо сложить все числа в наборе и разделить сумму на количество. Например, оценки школьника по информатике: 3, 4, 3, 5, 5. Что выходит за четверть: 4. Мы нашли среднее арифметическое по формуле: =(3+4+3+5+5)/5.
Как это быстро сделать с помощью функций Excel? Возьмем для примера ряд случайных чисел в строке:
Или: сделаем активной ячейку и просто вручную впишем формулу: =СРЗНАЧ(A1:A8).
Теперь посмотрим, что еще умеет функция СРЗНАЧ.
Найдем среднее арифметическое двух первых и трех последних чисел. Формула: =СРЗНАЧ(A1:B1;F1:h2). Результат:
Среднее значение по условию
Условием для нахождения среднего арифметического может быть числовой критерий или текстовый. Будем использовать функцию: =СРЗНАЧЕСЛИ().
Найти среднее арифметическое чисел, которые больше или равны 10.
Функция: =СРЗНАЧЕСЛИ(A1:A8;»>=10″)
Результат использования функции СРЗНАЧЕСЛИ по условию «>=10»:
Третий аргумент – «Диапазон усреднения» — опущен. Во-первых, он не обязателен. Во-вторых, анализируемый программой диапазон содержит ТОЛЬКО числовые значения. В ячейках, указанных в первом аргументе, и будет производиться поиск по прописанному во втором аргументе условию.
Внимание! Критерий поиска можно указать в ячейке. А в формуле сделать на нее ссылку.
Найдем среднее значение чисел по текстовому критерию. Например, средние продажи товара «столы».
Функция будет выглядеть так: =СРЗНАЧЕСЛИ($A$2:$A$12;A7;$B$2:$B$12). Диапазон – столбец с наименованиями товаров. Критерий поиска – ссылка на ячейку со словом «столы» (можно вместо ссылки A7 вставить само слово «столы»). Диапазон усреднения – те ячейки, из которых будут браться данные для расчета среднего значения.
В результате вычисления функции получаем следующее значение:
Внимание!
Для текстового критерия (условия) диапазон усреднения указывать обязательно.
Как посчитать средневзвешенную цену в Excel?
Как мы узнали средневзвешенную цену?
Формула: =СУММПРОИЗВ(C2:C12;B2:B12)/СУММ(C2:C12).
С помощью формулы СУММПРОИЗВ мы узнаем общую выручку после реализации всего количества товара. А функция СУММ — сумирует количесвто товара. Поделив общую выручку от реализации товара на общее количество единиц товара, мы нашли средневзвешенную цену. Этот показатель учитывает «вес» каждой цены. Ее долю в общей массе значений.
Среднее квадратическое отклонение: формула в Excel
Различают среднеквадратическое отклонение по генеральной совокупности и по выборке. В первом случае это корень из генеральной дисперсии. Во втором – из выборочной дисперсии.
Для расчета этого статистического показателя составляется формула дисперсии. Из нее извлекается корень. Но в Excel существует готовая функция для нахождения среднеквадратического отклонения.
Среднеквадратическое отклонение имеет привязку к масштабу исходных данных. Для образного представления о вариации анализируемого диапазона этого недостаточно. Чтобы получить относительный уровень разброса данных, рассчитывается коэффициент вариации:
Для образного представления о вариации анализируемого диапазона этого недостаточно. Чтобы получить относительный уровень разброса данных, рассчитывается коэффициент вариации:
среднеквадратическое отклонение / среднее арифметическое значение
Формула в Excel выглядит следующим образом:
СТАНДОТКЛОНП (диапазон значений) / СРЗНАЧ (диапазон значений).
Коэффициент вариации считается в процентах. Поэтому в ячейке устанавливаем процентный формат.
Проведение любого статистического анализа немыслимо без расчетов. В это статье рассмотрим, как рассчитать дисперсию, среднеквадратичное отклонение, коэффиент вариации и другие статистические показатели в Excel.
Максимальное и минимальное значение
Среднее линейное отклонение
Среднее линейное отклонение представляет собой среднее из абсолютных (по модулю) отклонений от в анализируемой совокупности данных. Математическая формула имеет вид:
a – среднее линейное отклонение,
X – анализируемый показатель,
X̅ – среднее значение показателя,
n
В Эксель эта функция называется СРОТКЛ .
После выбора функции СРОТКЛ указываем диапазон данных, по которому должен произойти расчет. Нажимаем «ОК».
Дисперсия
{module 111}
Возможно, не все знают, что такое , поэтому поясню, — это мера, характеризующая разброс данных вокруг математического ожидания. Однако в распоряжении обычно есть только выборка, поэтому используют следующую формулу дисперсии:
s 2 – выборочная дисперсия, рассчитанная по данным наблюдений,
X – отдельные значения,
X̅ – среднее арифметическое по выборке,
n – количество значений в анализируемой совокупности данных.
Соответствующая функция Excel — ДИСП.Г . При анализе относительно небольших выборок (примерно до 30-ти наблюдений) следует использовать , которая рассчитывается по следующей формуле.
Отличие, как видно, только в знаменателе. В Excel для расчета выборочной несмещенной дисперсии есть функция ДИСП.В .
Выбираем нужный вариант (генеральную или выборочную), указываем диапазон, жмем кнопку «ОК». Полученное значение может оказаться очень большим из-за предварительного возведения отклонений в квадрат. Дисперсия в статистике очень важный показатель, но ее обычно используют не в чистом виде, а для дальнейших расчетов.
Полученное значение может оказаться очень большим из-за предварительного возведения отклонений в квадрат. Дисперсия в статистике очень важный показатель, но ее обычно используют не в чистом виде, а для дальнейших расчетов.
Среднеквадратичное отклонение
Среднеквадратичное отклонение (СКО) – это корень из дисперсии. Этот показатель также называют стандартным отклонением и рассчитывают по формуле:
по генеральной совокупности
по выборке
Можно просто извлечь корень из дисперсии, но в Excel для среднеквадратичного отклонения есть готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).
Стандартное и среднеквадратичное отклонение, повторюсь, — синонимы.
Далее, как обычно, указываем нужный диапазон и нажимаем на «ОК». Среднеквадратическое отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными. Об этом ниже.
Коэффициент вариации
Все показатели, рассмотренные выше, имеют привязку к масштабу исходных данных и не позволяют получить образное представление о вариации анализируемой совокупности. Для получения относительной меры разброса данных используют коэффициент вариации , который рассчитывается путем деления среднеквадратичного отклонения на среднее арифметическое . Формула коэффициента вариации проста:
Для расчета коэффициента вариации в Excel нет готовой функции, что не есть большая проблема. Расчет можно произвести простым делением стандартного отклонения на среднее значение. Для этого в строке формул пишем:
СТАНДОТКЛОН.Г()/СРЗНАЧ()
В скобках указывается диапазон данных. При необходимости используют среднее квадратичное отклонение по выборке (СТАНДОТКЛОН.В).
Коэффициент вариации обычно выражается в процентах, поэтому ячейку с формулой можно обрамить процентным форматом. Нужная кнопка находится на ленте на вкладке «Главная»:
Изменить формат также можно, выбрав из контекстного меню после выделения нужной ячейки и нажатия правой кнопкой мышки.
Коэффициент вариации, в отличие от других показателей разброса значений, используется как самостоятельный и весьма информативный индикатор вариации данных. В статистике принято считать, что если коэффициент вариации менее 33%, то совокупность данных является однородной, если более 33%, то – неоднородной. Эта информация может быть полезна для предварительного описания данных и определения возможностей проведения дальнейшего анализа. Кроме того, коэффициент вариации, измеряемый в процентах, позволяет сравнивать степень разброса различных данных независимо от их масштаба и единиц измерений. Полезное свойство.
Коэффициент осцилляции
Еще один показатель разброса данных на сегодня — коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.
Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.
В целом, с помощью Excel многие статистические показатели рассчитываются очень просто. Если что-то непонятно, всегда можно воспользоваться окошком для поиска во вставке функций. Ну, и Гугл в помощь.
Добрый день!
В статье я решил рассмотреть, как работает стандартное отклонение в Excel с помощью функции СТАНДОТКЛОН. Я просто очень давно не описывал и не комментировал , а еще просто потому что это очень полезная функция для тех, кто изучает высшую математику. А оказать помощь студентам – это святое, по себе знаю, как трудно она осваивается. В реальности функции стандартных отклонений можно использовать для определения стабильности продаваемой продукции, создания цены, корректировки или формирования ассортимента, ну и других не менее полезных анализов ваших продаж.
В Excel используются несколько вариантов этой функции отклонения:
Математическая теория
Для начала немножко о теории, как математическим языком можно описать функцию стандартного отклонения для применения ее в Excel, для анализа, к примеру, данных статистики продаж, но об этом дальше. Предупреждаю сразу, буду писать очень много непонятных слов…)))), если что ниже по тексту смотрите сразу практическое применение в программе.
Предупреждаю сразу, буду писать очень много непонятных слов…)))), если что ниже по тексту смотрите сразу практическое применение в программе.
Что же собственно делает стандартное отклонение? Оно производит оценку среднеквадратического отклонения случайной величины Х относительно её математического ожидания на основе несмещённой оценки её дисперсии. Согласитесь, звучит запутанно, но я думаю учащиеся поймут о чём собственно идет речь!
Для начала нам нужно определить «среднеквадратическое отклонение», что бы в дальнейшем произвести расчёт «стандартного отклонения», в этом нам поможет формула: Описать формулу возможно так: будет измеряться в тех же единицах что и измерения случайной величины и применяется при вычислении стандартной среднеарифметической ошибки, когда производятся построения доверительных интервалов, при проверке гипотез на статистику или же при анализе линейной взаимосвязи между независимыми величинами. Функцию определяют, как квадратный корень из дисперсии независимых величин.
Теперь можно дать определение и стандартному отклонению – это анализ среднеквадратического отклонения случайной величины Х сравнительно её математической перспективы на основе несмещённой оценки её дисперсии. Формула записывается так:
Отмечу, что все две оценки предоставляются смещёнными. При общих случаях построить несмещённую оценку не является возможным. Но оценка на основе оценки несмещённой дисперсии будет состоятельной.
Ну а теперь отойдём от скучной теории и на практике посмотрим, как работает функция СТАНДОТКЛОН. Я не буду рассматривать все вариации функции стандартного отклонения в Excel, достаточно и одной, но в примерах. А для примера рассмотрим, как определяется статистика стабильности продаж.
Для начала посмотрите на орфографию функции, а она как вы видите, очень проста:
СТАНДОТКЛОН.Г(_число1_;_число2_; ….), где:
Теперь создадим файл примера и на его основе рассмотрим работу этой функции. Так как для проведения аналитических вычислений необходимо использовать не меньше трёх значений, как в принципе в любом статистическом анализе, то и я взял условно 3 периода, это может быть год, квартал, месяц или неделя. В моем случае – месяц. Для наибольшей достоверности рекомендую брать как можно большое количество периодов, но никак не менее трёх. Все данные в таблице очень простые для наглядности работы и функциональности формулы.
Так как для проведения аналитических вычислений необходимо использовать не меньше трёх значений, как в принципе в любом статистическом анализе, то и я взял условно 3 периода, это может быть год, квартал, месяц или неделя. В моем случае – месяц. Для наибольшей достоверности рекомендую брать как можно большое количество периодов, но никак не менее трёх. Все данные в таблице очень простые для наглядности работы и функциональности формулы.
Для начала нам необходимо посчитать среднее значение по месяцам. Будем использовать для этого функцию СРЗНАЧ и получится формула: =СРЗНАЧ(C4:E4).
Теперь собственно мы и можем найти стандартное отклонение с помощью функции СТАНДОТКЛОН.Г в значении которой нужно проставить продажи товара каждого периода. Получится формула следующего вида: =СТАНДОТКЛОН.Г(C4;D4;E4).
Ну вот и сделана половина дел. Следующим шагом мы формируем «Вариацию», это получается делением на среднее значение, стандартного отклонения и результат переводим в проценты. Получаем такую таблицу:
Ну вот основные расчёты окончены, осталось разобраться как идут продажи стабильно или нет. Возьмем как условие что отклонения в 10% это считается стабильно, от 10 до 25% это небольшие отклонения, а вот всё что выше 25% это уже не стабильно. Для получения результата по условиям воспользуемся логической и для получения результата напишем формулу:
Возьмем как условие что отклонения в 10% это считается стабильно, от 10 до 25% это небольшие отклонения, а вот всё что выше 25% это уже не стабильно. Для получения результата по условиям воспользуемся логической и для получения результата напишем формулу:
ЕСЛИ(h5
Все диапазоны взяты условно для наглядности, у ваших задач могут быть совсем другие условия.
Для улучшения визуализации данных, когда ваша таблица имеет тысячи позиций стоит воспользоваться возможностью , наложить по неким условиям, которые вам нужны или же использовать , что бы цветовой гаммой выделить определенные варианты, это будет очень наглядно.
Для начала выделяете , для которых будете применяться условное форматирование. В панели управления «Главная» выбираете «Условное форматирование» и в выпадающем меню пункт «Правила выделения ячеек» и следующим нажимаете пункт меню «Текст содержит…». Появляется диалоговое окно в которое вы вписываете свои условия.
После того как прописали условия, к примеру, «стабильно» — зелёный цвет, «нормально» — жёлтый и «не стабильно» — красный, получим красивую и понятную таблицу в которой видно на что в первую очередь обращать внимание. 2 «вычисляем сумму квадратов разницы элементов массива и среднего значения
Next x
MyStDevP = Sqr(tmp / aCnt) «вычисляем СТАНДОТКЛОН.Г()
End Function
2 «вычисляем сумму квадратов разницы элементов массива и среднего значения
Next x
MyStDevP = Sqr(tmp / aCnt) «вычисляем СТАНДОТКЛОН.Г()
End Function
Function MyStDevP (Arr ) Dim x , aCnt & , aSum #, aAver#, tmp# For Each x In Arr aSum = aSum + x «вычисляем сумму элементов массива |
Среди множества показателей, которые применяются в статистике, нужно выделить расчет дисперсии. Следует отметить, что выполнение вручную данного вычисления – довольно утомительное занятие. К счастью, в приложении Excel имеются функции, позволяющие автоматизировать процедуру расчета. Выясним алгоритм работы с этими инструментами.
Дисперсия – это показатель вариации, который представляет собой средний квадрат отклонений от математического ожидания. Таким образом, он выражает разброс чисел относительно среднего значения. Вычисление дисперсии может проводиться как по генеральной совокупности, так и по выборочной.
Способ 1: расчет по генеральной совокупности
Для расчета данного показателя в Excel по генеральной совокупности применяется функция ДИСП.Г . Синтаксис этого выражения имеет следующий вид:
ДИСП.Г(Число1;Число2;…)
Всего может быть применено от 1 до 255 аргументов. В качестве аргументов могут выступать, как числовые значения, так и ссылки на ячейки, в которых они содержатся.
Посмотрим, как вычислить это значение для диапазона с числовыми данными.
Способ 2: расчет по выборке
В отличие от вычисления значения по генеральной совокупности, в расчете по выборке в знаменателе указывается не общее количество чисел, а на одно меньше. Это делается в целях коррекции погрешности. Эксель учитывает данный нюанс в специальной функции, которая предназначена для данного вида вычисления – ДИСП.В. Её синтаксис представлен следующей формулой:
ДИСП.В(Число1;Число2;…)
Количество аргументов, как и в предыдущей функции, тоже может колебаться от 1 до 255.
Как видим, программа Эксель способна в значительной мере облегчить расчет дисперсии. Эта статистическая величина может быть рассчитана приложением, как по генеральной совокупности, так и по выборке. При этом все действия пользователя фактически сводятся только к указанию диапазона обрабатываемых чисел, а основную работу Excel делает сам. Безусловно, это сэкономит значительное количество времени пользователей.
Нам приходится сталкиваться с расчётом таких значений, как дисперсия, среднеквадратичное отклонение и, разумеется, коэффициент вариации. Именно расчёту последнего стоит уделить особое внимание. Очень важно, чтобы каждый новичок, который только приступает к работе с табличным редактором, мог быстро подсчитать относительную границу разброса значений.
Что такое коэффициент вариации и для чего он нужен?
Итак, как мне кажется, нелишним будет провести небольшой теоретический экскурс и разобраться в природе коэффициента вариации. Этот показатель необходим для отражения диапазона данных относительно среднего значения. Иными словами, он показывает отношение стандартного отклонения к среднему значению. Коэффициент вариации принято измерять в процентном выражении и отображать с его помощью однородность временного ряда.
Иными словами, он показывает отношение стандартного отклонения к среднему значению. Коэффициент вариации принято измерять в процентном выражении и отображать с его помощью однородность временного ряда.
Коэффициент вариации станет незаменимым помощником в том случае, когда вам необходимо будет сделать прогноз по данным из заданной выборки. Этот индикатор выделит главные ряды значений, которые будут наиболее полезными для последующего прогнозирования, а также очистит выборку от малозначительных факторов. Так, если вы видите, что значение коэффициента равно 0%, то с уверенностью заявляйте о том, что ряд является однородным, а значит, все значения в нём равны один с другим. В случае, если коэффициент вариации принимает значение, превышающее отметку в 33%, то это говорит о том, что вы имеете дело с неоднородным рядом, в котором отдельные значения существенно отличаются от среднего показателя выборки.
Как найти среднее квадратичное отклонение?
Поскольку для расчёта показателя вариации в Excel нам необходимо использовать среднее квадратичное отклонение, то вполне уместно будет выяснить, как нам посчитать этот параметр.
Из школьного курса алгебры мы знаем, что среднее квадратичное отклонение — это извлечённый из дисперсии квадратный корень, то есть этот показатель определяет степень отклонения конкретного показателя общей выборки от её среднего значения. С его помощью мы можем измерить абсолютную меру колебания изучаемого признака и чётко её интерпретировать.
Рассчитываем коэффициент в Экселе
К сожалению, в Excel не заложена стандартная формула , которая бы позволила рассчитать показатель вариации автоматически. Но это не значит, что вам придётся производить расчёты в уме. Отсутствие шаблона в «Строке формул» никоим образом не умаляет способностей Excel, потому вы вполне сможете заставить программу выполнить необходимый вам расчёт, прописав соответствующую команду вручную.
Для того чтобы рассчитать показатель вариации в Excel, необходимо вспомнить школьный курс математики и разделить стандартное отклонение на среднее значение выборки. То есть на деле формула выглядит следующим образом — СТАНДОТКЛОН(заданный диапазон данных)/СРЗНАЧ(заданный диапазон данных). Ввести эту формулу необходимо в ту ячейку Excel, в которой вы хотите получить нужный вам расчёт.
Ввести эту формулу необходимо в ту ячейку Excel, в которой вы хотите получить нужный вам расчёт.
Не забывайте и о том, что поскольку коэффициент выражается в процентах, то ячейке с формулой нужно будет задать соответствующий формат. Сделать это можно следующим образом:
- Откройте вкладку «Главная».
- Найдите в ней категорию «Формат ячеек » и выберите необходимый параметр.
Как вариант, можно задать процентный формат ячейке при помощи клика по правой кнопке мыши на активированной клеточке таблицы. В появившемся контекстном меню, аналогично вышеуказанному алгоритму нужно выбрать категорию «Формат ячейки» и задать необходимое значение.
Выберите «Процентный», а при необходимости укажите число десятичных знаков
Возможно, кому-то вышеописанный алгоритм покажется сложным. На самом же деле расчёт коэффициента так же прост, как сложение двух натуральных чисел. Единожды выполнив эту задачу в Экселе, вы больше никогда не вернётесь к утомительным многосложным решениям в тетрадке.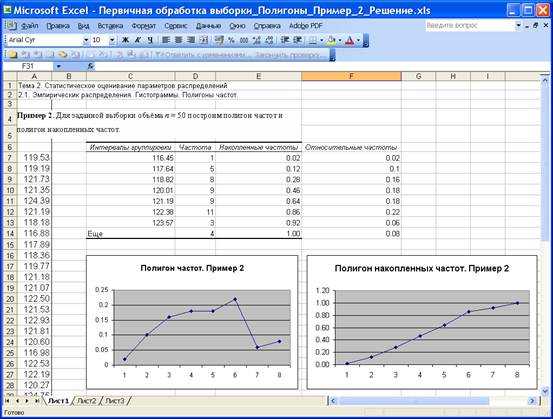
Всё ещё не можете сделать качественное сравнение степени разброса данных? Теряетесь в масштабах выборки? Тогда прямо сейчас принимайтесь за дело и осваивайте на практике весь теоретический материал, который был изложен выше! Пусть статистический анализ и разработка прогноза больше не вызывают у вас страха и негатива. Экономьте свои силы и время вместе с
Как провести XYZ анализ товарных запасов в Excel
Анализ оборачиваемости
Финансовые коэффициенты
Инвестиционный анализ
МСФО и консолидация
Управление запасами
Управление затратами
Внутренний контроль
Семинары
Управленческий учет
Об Excel программах
В целях оптимизации ассортимента компании проводится XYZ анализ товарных запасов. Методика применяется в совокупности с ABC-анализом и заключается в классификации товаров в зависимости от потребностей покупателей. На основании результатов расчетов прогнозируются закупки и продажи.
Как выполняется XYZ анализ ассортимента
Наряду с методом ABC XYZ анализ проводится для ранжирования ресурсов компании. Если речь идет о товарных запасах, первый бизнес анализ помогает классифицировать ресурсы по уровню (степени) их важности. При этом запасы делятся на следующие группы:
Если речь идет о товарных запасах, первый бизнес анализ помогает классифицировать ресурсы по уровню (степени) их важности. При этом запасы делятся на следующие группы:
- А – наиболее ценные виды товаров (около 20 %) приносят организации большую часть продаж (около 80 %).
- В – промежуточные товары (около 30 %) приносят около 15 % реализации.
- С – наименее ценные товарные позиции (около 50 %) приносят 5 % реализации.
XYZ анализ позволяет группировать ресурсы по степени их нужности организации, то есть в зависимости от интенсивности и стабильности их потребления.
В процессе расчетов образуется также три основные группы – X, Y и Z. Товары распределяются по возрастанию в зависимости от коэффициента вариации. Это относительный статистический показатель, который измеряется в % и используется для сравнения не связанных между собой данных. Позволяет построить финансовую модель с учетом унифицированного риска.
Общая формула расчета:
К вариации = Среднеквадратическое отклонение случайной величины / Среднее значение случайной величины.
Формула расчета для товарного ассортимента:
где:
где Хi — величина объема продаж по отдельному товару за i-й период;
х — среднее значение объема продаж по анализируемой позиции;
n — количество заданных периодов.
При проведении расчетов К вариации определяется по каждой из анализируемой позиции отдельно. Затем оцениваются полученные отклонения продаж от среднего значения. После ассортимент ранжируется по группам – X, Y и Z. Каждая из полученных групп классифицируется так:
-
X – такие ресурсы характеризуются наиболее стабильным спросом, высоким уровнем потребления, а значит, значительными продажами и достоверными результатами прогнозирования. Компании не грозят убытки даже при закупке значительных партий этих товаров.
 На их долю приходится до 10 % от общих объемов ресурсов.
На их долю приходится до 10 % от общих объемов ресурсов. - Y – это ресурсы, которые отличаются известными колебаниями в потреблении, но все равно остаются достаточно надежными для организации. В качестве причины колебания выступает, к примеру, сезонный спрос. Для точности прогнозов требуется углубленный анализ и контроль статистики продаж, оптимизация складских запасов. На долю данной группы приходится 11-25 % от общих объемов ресурсов.
- Z – ресурсы последней группы имеют самый волатильный спрос, отличаются нерегулярными продажами и сложным прогнозированием. Такие позиции рекомендуется выводить из ассортимента или работать с ними по предзаказу. Коэффициент вариации имеет значение от 25 %.
В процессе расчетов аналитику нужно помнить о том, что реальные значения К вариации могут отличаться от полученных. Поскольку сам по себе этот коэффициент является относительным, его могут искажать конкретные условия продаж, влияющие на потребность. К примеру, это сезонность спроса, проведение различных акций, отнесение к дефицитным позициям, попадание в тренд и т.д.
К примеру, это сезонность спроса, проведение различных акций, отнесение к дефицитным позициям, попадание в тренд и т.д.
Затем, на основании исходных данных, определяют наиболее популярные среди покупателей товары, наименее популярные и средние. Для этого по каждому наименованию рассчитывается К вариации. Номенклатура классифицируется по 3 основным группам:
- X – приносят максимальную прибыль магазину, пользуются стабильно высоким спросом у покупателей.
- Y – отличаются умеренным спросом, приносят регулярную прибыль. Продажи подвержены сезонным колебаниям.
-
Z – характеризуются небольшим спросом, приносят незначительную прибыль. Продажи можно совсем убрать или сократить.
Пример проведения XYZ анализа в Excel
Прежде чем переходить к расчетам, определите анализируемые товарную номенклатуру и временной интервал. Методику можно применить ко всей продукции, к основному ассортименту или к отдельным группам ресурсов. Периодом для расчетов рекомендуется назначить длительный интервал времени для повышения точности результатов. По итогам данные распределяются по группам в виде таблицы и графиков.
Периодом для расчетов рекомендуется назначить длительный интервал времени для повышения точности результатов. По итогам данные распределяются по группам в виде таблицы и графиков.
Расчеты коэффициента вариации не нужно выполнять вручную. Рекомендуется использовать для вычислений табличные возможности автоматизированных сервисов, к примеру, Excel. Рассмотрим как построить финансовую модель в Excel.
Программы, представленные на нашем сайте позволяют автоматически провести XYZ анализ. Для анализа все данные за выбранный временный интервал импортируются в Excel-программу из 1С, путем выгрузки стандартного отчета “Анализ счета» в разрезе анализируемых позиций.
На основании этих сведений программа определяет коэффициенты вариации, ранжирует номенклатуру по XYZ-методу. Визуализация ассортимента с помощью графиков наглядно показывает, какие товары являются лидерами продаж, а какие относятся к аутсайдерам.
Последовательное внедрение в бизнес-процессы управленческих решений сообразно расчетам помогает менеджерам ориентироваться в закупках при разработке товарного ассортимента:
-
Товары группы X – те, которые максимально привлекают клиентов.
 Всегда должны быть в наличии (выделены желтым цветом на рисунке). Спрос на такие товары стабильный, он не имеет сезонных колебаний и относительно постоянный.
Всегда должны быть в наличии (выделены желтым цветом на рисунке). Спрос на такие товары стабильный, он не имеет сезонных колебаний и относительно постоянный. - Товары группы Y – имеют стабильный спрос, который существенно подвержен сезонным колебаниям.
- Товары группы Z – отличаются случайным спросом. Компания ничего не потеряет, если откажется от их реализации. В крайнем случае можно работать с этими товарами по предоплате.
Аналитическая Excel-таблица учитывает все нюансы расчетов, которые сложно упомнить при ручных вычислениях. Прежде всего, это сезонность спроса. Модель позволяет при необходимости исключить из расчетов исходные данные по выбранным месяцам колебания продаж – при помощи ввода специального коэффициента продажи каждого месяца корректируются на сезонный коэффициент. В итоге получаются более точные результаты, что помогает определить реальный прогноз. Информация по сезонам обрабатывается отдельно. Дополнительно программа проводит анализ оборачиваемости запасов, дебиторских и кредиторских обязательств, затрат, финансового цикла и т. д.
д.
К списку записей
5
Похожие статьи
Управление размером буфера товарных запасов на основе коэффициента оборачиваемости
Поддержание оптимального для организации уровня запасов обеспечивает высокую рентабельность бизнеса. Управление буфером запасов помогает избежать перебоев с закупками и упущенных продаж, а также появления неликвидных запасов на складах. Для этих целей используются принципы теории ограничений, которые могут применяться в торговых, производственных, дистрибуционных компаниях, а также в ритейле.
Управление запасами по теории ограничений (TOC) в Power BI и Excel
Инновационная Excel модель, которая рассчитывает нужное количество товара, автоматизирует рутинные функции управления запасами, предоставляет необходимую аналитику, а также инструменты для управления ассортиментом. Работает на основе выгрузок стандартных отчетов из 1С:Предприятие
Анализ движения запасов и системы управления запасами в Excel
Современную торговлю трудно представить без налаженных инструментов автоматического заказа товаров. Говоря о товарах, подразумеваются не только изделия для перепродажи, но и другие ценности – материалы, сырье, полуфабрикаты и т.д. Наличие адаптированной к потребностям деятельности системы управления запасами не является редкостью в зарубежных компаниях. Однако многие российские предприятия даже не знают, что это такое.
Говоря о товарах, подразумеваются не только изделия для перепродажи, но и другие ценности – материалы, сырье, полуфабрикаты и т.д. Наличие адаптированной к потребностям деятельности системы управления запасами не является редкостью в зарубежных компаниях. Однако многие российские предприятия даже не знают, что это такое.
ABC-анализ дебиторской задолженности и продаж
АВС-анализ – это классический метод ранжирования дебиторской задолженности (или других активов компании) по заданным факторам. Наиболее часто в качестве расчетных критериев используются возраст или объем задолженности. Методика может применяться при управлении оборачиваемостью любыми ресурсами, включая валовую прибыль или валовые продажи.
Графики отклонение от среднего в excel. Дисперсия, ее виды, среднеквадратическое отклонение. Как найти среднее арифметическое чисел
Понятие процент отклонения подразумевает разницу между двумя числовыми значениями в процентах. Приведем конкретный пример: допустим одного дня с оптового склада было продано 120 штук планшетов, а на следующий день – 150 штук. Разница в объемах продаж – очевидна, на 30 штук больше продано планшетов в следующий день. При вычитании от 150-ти числа 120 получаем отклонение, которое равно числу +30. Возникает вопрос: чем же является процентное отклонение?
Приведем конкретный пример: допустим одного дня с оптового склада было продано 120 штук планшетов, а на следующий день – 150 штук. Разница в объемах продаж – очевидна, на 30 штук больше продано планшетов в следующий день. При вычитании от 150-ти числа 120 получаем отклонение, которое равно числу +30. Возникает вопрос: чем же является процентное отклонение?
Как посчитать отклонение в процентах в Excel
Процент отклонения вычисляется через вычитание старого значения от нового значения, а далее деление результата на старое значение. Результат вычисления этой формулы в Excel должен отображаться в процентном формате ячейки. В данном примере формула вычисления выглядит следующим образом (150-120)/120=25%. Формулу легко проверить 120+25%=150.
Обратите внимание! Если мы старое и новое число поменяем местами, то у нас получиться уже формула для вычисления наценки .
Ниже на рисунке представлен пример, как выше описанное вычисление представить в виде формулы Excel. Формула в ячейке D2 вычисляет процент отклонения между значениями продаж для текущего и прошлого года: =(C2-B2)/B2
Важно обратит внимание в данной формуле на наличие скобок. По умолчанию в Excel операция деления всегда имеет высший приоритет по отношению к операции вычитания. Поэтому если мы не поставим скобки, тогда сначала будет разделено значение, а потом из него вычитается другое значение. Такое вычисление (без наличия скобок) будет ошибочным. Закрытие первой части вычислений в формуле скобками автоматически повышает приоритет операции вычитания выше по отношению к операции деления.
По умолчанию в Excel операция деления всегда имеет высший приоритет по отношению к операции вычитания. Поэтому если мы не поставим скобки, тогда сначала будет разделено значение, а потом из него вычитается другое значение. Такое вычисление (без наличия скобок) будет ошибочным. Закрытие первой части вычислений в формуле скобками автоматически повышает приоритет операции вычитания выше по отношению к операции деления.
Правильно со скобками введите формулу в ячейку D2, а далее просто скопируйте ее в остальные пустые ячейки диапазона D2:D5. Чтобы скопировать формулу самым быстрым способом, достаточно подвести курсор мышки к маркеру курсора клавиатуры (к нижнему правому углу) так, чтобы курсор мышки изменился со стрелочки на черный крестик. После чего просто сделайте двойной щелчок левой кнопкой мышки и Excel сам автоматически заполнит пустые ячейки формулой при этом сам определит диапазон D2:D5, который нужно заполнить до ячейки D5 и не более. Это очень удобный лайфхак в Excel.
Альтернативная формула для вычисления процента отклонения в Excel
В альтернативной формуле, вычисляющей относительное отклонение значений продаж с текущего года сразу делиться на значения продаж прошлого года, а только потом от результата отнимается единица: =C2/B2-1.
Как видно на рисунке результат вычисления альтернативной формулы такой же, как и в предыдущей, а значит правильный. Но альтернативную формулу легче записать, хот и возможно для кого-то сложнее прочитать так чтобы понять принцип ее действия. Или сложнее понять, какое значение выдает в результате вычисления данная формула если он не подписан.
Единственный недостаток данной альтернативной формулы – это отсутствие возможности рассчитать процентное отклонение при отрицательных числах в числителе или в заменителе. Даже если мы будем использовать в формуле функцию ABS, то формула будет возвращать ошибочный результат при отрицательном числе в заменителе.
Так как в Excel по умолчанию приоритет операции деления выше операции вычитания в данной формуле нет необходимости применять скобки.
Нам приходится сталкиваться с расчётом таких значений, как дисперсия, среднеквадратичное отклонение и, разумеется, коэффициент вариации. Именно расчёту последнего стоит уделить особое внимание. Очень важно, чтобы каждый новичок, который только приступает к работе с табличным редактором, мог быстро подсчитать относительную границу разброса значений.
Очень важно, чтобы каждый новичок, который только приступает к работе с табличным редактором, мог быстро подсчитать относительную границу разброса значений.
Что такое коэффициент вариации и для чего он нужен?
Итак, как мне кажется, нелишним будет провести небольшой теоретический экскурс и разобраться в природе коэффициента вариации. Этот показатель необходим для отражения диапазона данных относительно среднего значения. Иными словами, он показывает отношение стандартного отклонения к среднему значению. Коэффициент вариации принято измерять в процентном выражении и отображать с его помощью однородность временного ряда.
Коэффициент вариации станет незаменимым помощником в том случае, когда вам необходимо будет сделать прогноз по данным из заданной выборки. Этот индикатор выделит главные ряды значений, которые будут наиболее полезными для последующего прогнозирования, а также очистит выборку от малозначительных факторов. Так, если вы видите, что значение коэффициента равно 0%, то с уверенностью заявляйте о том, что ряд является однородным, а значит, все значения в нём равны один с другим. В случае, если коэффициент вариации принимает значение, превышающее отметку в 33%, то это говорит о том, что вы имеете дело с неоднородным рядом, в котором отдельные значения существенно отличаются от среднего показателя выборки.
В случае, если коэффициент вариации принимает значение, превышающее отметку в 33%, то это говорит о том, что вы имеете дело с неоднородным рядом, в котором отдельные значения существенно отличаются от среднего показателя выборки.
Как найти среднее квадратичное отклонение?
Поскольку для расчёта показателя вариации в Excel нам необходимо использовать среднее квадратичное отклонение, то вполне уместно будет выяснить, как нам посчитать этот параметр.
Из школьного курса алгебры мы знаем, что среднее квадратичное отклонение — это извлечённый из дисперсии квадратный корень, то есть этот показатель определяет степень отклонения конкретного показателя общей выборки от её среднего значения. С его помощью мы можем измерить абсолютную меру колебания изучаемого признака и чётко её интерпретировать.
Рассчитываем коэффициент в Экселе
К сожалению, в Excel не заложена стандартная формула , которая бы позволила рассчитать показатель вариации автоматически. Но это не значит, что вам придётся производить расчёты в уме. Отсутствие шаблона в «Строке формул» никоим образом не умаляет способностей Excel, потому вы вполне сможете заставить программу выполнить необходимый вам расчёт, прописав соответствующую команду вручную.
Отсутствие шаблона в «Строке формул» никоим образом не умаляет способностей Excel, потому вы вполне сможете заставить программу выполнить необходимый вам расчёт, прописав соответствующую команду вручную.
Для того чтобы рассчитать показатель вариации в Excel, необходимо вспомнить школьный курс математики и разделить стандартное отклонение на среднее значение выборки. То есть на деле формула выглядит следующим образом — СТАНДОТКЛОН(заданный диапазон данных)/СРЗНАЧ(заданный диапазон данных). Ввести эту формулу необходимо в ту ячейку Excel, в которой вы хотите получить нужный вам расчёт.
Не забывайте и о том, что поскольку коэффициент выражается в процентах, то ячейке с формулой нужно будет задать соответствующий формат. Сделать это можно следующим образом:
- Откройте вкладку «Главная».
- Найдите в ней категорию «Формат ячеек » и выберите необходимый параметр.
Как вариант, можно задать процентный формат ячейке при помощи клика по правой кнопке мыши на активированной клеточке таблицы. В появившемся контекстном меню, аналогично вышеуказанному алгоритму нужно выбрать категорию «Формат ячейки» и задать необходимое значение.
В появившемся контекстном меню, аналогично вышеуказанному алгоритму нужно выбрать категорию «Формат ячейки» и задать необходимое значение.
Выберите «Процентный», а при необходимости укажите число десятичных знаков
Возможно, кому-то вышеописанный алгоритм покажется сложным. На самом же деле расчёт коэффициента так же прост, как сложение двух натуральных чисел. Единожды выполнив эту задачу в Экселе, вы больше никогда не вернётесь к утомительным многосложным решениям в тетрадке.
Всё ещё не можете сделать качественное сравнение степени разброса данных? Теряетесь в масштабах выборки? Тогда прямо сейчас принимайтесь за дело и осваивайте на практике весь теоретический материал, который был изложен выше! Пусть статистический анализ и разработка прогноза больше не вызывают у вас страха и негатива. Экономьте свои силы и время вместе с
В данной статье я расскажу о том, как найти среднеквадратическое отклонение . Этот материал крайне важен для полноценного понимания математики, поэтому репетитор по математике должен посвятить его изучению отдельный урок или даже несколько. В этой статье вы найдёте ссылку на подробный и понятный видеоурок, в котором рассказано о том, что такое среднеквадратическое отклонение и как его найти.
В этой статье вы найдёте ссылку на подробный и понятный видеоурок, в котором рассказано о том, что такое среднеквадратическое отклонение и как его найти.
Среднеквадратическое отклонение дает возможность оценить разброс значений, полученных в результате измерения какого-то параметра. Обозначается символом (греческая буква «сигма»).
Формула для расчета довольно проста. Чтобы найти среднеквадратическое отклонение, нужно взять квадратный корень из дисперсии. Так что теперь вы должны спросить: “А что же такое дисперсия?”
Что такое дисперсия
Определение дисперсии звучит так. Дисперсия — это среднее арифметическое от квадратов отклонений значений от среднего.
Чтобы найти дисперсию последовательно проведите следующие вычисления:
- Определите среднее (простое среднее арифметическое ряда значений).
- Затем от каждого из значений отнимите среднее и возведите полученную разность в квадрат (получили квадрат разности ).
- Следующим шагом будет вычисление среднего арифметического полученных квадратов разностей (Почему именно квадратов вы сможете узнать ниже).

Рассмотрим на примере. Допустим, вы с друзьями решили измерить рост ваших собак (в миллиметрах). В результате измерений вы получили следующие данные измерений роста (в холке): 600 мм, 470 мм, 170 мм, 430 мм и 300 мм.
Вычислим среднее значение, дисперсию и среднеквадратическое отклонение.
Сперва найдём среднее значение . Как вы уже знаете, для этого нужно сложить все измеренные значения и поделить на количество измерений. Ход вычислений:
Среднее мм.
Итак, среднее (среднеарифметическое) составляет 394 мм.
Теперь нужно определить отклонение роста каждой из собак от среднего :
Наконец, чтобы вычислить дисперсию , каждую из полученных разностей возводим в квадрат, а затем находим среднее арифметическое от полученных результатов:
Дисперсия мм 2 .
Таким образом, дисперсия составляет 21704 мм 2 .
Как найти среднеквадратическое отклонение
Так как же теперь вычислить среднеквадратическое отклонение, зная дисперсию? Как мы помним, взять из нее квадратный корень. То есть среднеквадратическое отклонение равно:
То есть среднеквадратическое отклонение равно:
Мм (округлено до ближайшего целого значения в мм).
Применив данный метод, мы выяснили, что некоторые собаки (например, ротвейлеры) – очень большие собаки. Но есть и очень маленькие собаки (например, таксы, только говорить им этого не стоит).
Самое интересное, что среднеквадратическое отклонение несет в себе полезную информацию. Теперь мы можем показать, какие из полученных результатов измерения роста находятся в пределах интервала, который мы получим, если отложим от среднего (в обе стороны от него) среднеквадратическое отклонение.
То есть с помощью среднеквадратического отклонения мы получаем “стандартный” метод, который позволяет узнать, какое из значений является нормальным (среднестатистическим), а какое экстраординарно большим или, наоборот, малым.
Что такое стандартное отклонение
Но… все будет немного иначе, если мы будем анализировать выборку данных. В нашем примере мы рассматривали генеральную совокупность. То есть наши 5 собак были единственными в мире собаками, которые нас интересовали.
То есть наши 5 собак были единственными в мире собаками, которые нас интересовали.
Но если данные являются выборкой (значениями, которые выбрали из большой генеральной совокупности), тогда вычисления нужно вести иначе.
Если есть значений, то:
Все остальные расчеты производятся аналогично, в том числе и определение среднего.
Например, если наших пять собак – только выборка из генеральной совокупности собак (всех собак на планете), мы должны делить на 4, а не на 5, а именно:
Дисперсия выборки = мм 2 .
При этом стандартное отклонение по выборке равно мм (округлено до ближайшего целого значения).
Можно сказать, что мы произвели некоторую “коррекцию” в случае, когда наши значения являются всего лишь небольшой выборкой.
Примечание. Почему именно квадраты разностей?
Но почему при вычислении дисперсии мы берём именно квадраты разностей? Допустим при измерении какого-то параметра, вы получили следующий набор значений: 4; 4; -4; -4. Если мы просто сложим абсолютные отклонения от среднего (разности) между собой … отрицательные значения взаимно уничтожатся с положительными:
Если мы просто сложим абсолютные отклонения от среднего (разности) между собой … отрицательные значения взаимно уничтожатся с положительными:
.
Получается, этот вариант бесполезен. Тогда, может, стоит попробовать абсолютные значения отклонений (то есть модули этих значений)?
На первый взгляд получается неплохо (полученная величина, кстати, называется средним абсолютным отклонением), но не во всех случаях. Попробуем другой пример. Пусть в результате измерения получился следующий набор значений: 7; 1; -6; -2. Тогда среднее абсолютное отклонение равно:
Вот это да! Снова получили результат 4, хотя разности имеют гораздо больший разброс.
А теперь посмотрим, что получится, если возвести разности в квадрат (и взять потом квадратный корень из их суммы).
Для первого примера получится:
.
Для второго примера получится:
Теперь – совсем другое дело! Среднеквадратическое отклонение получается тем большим, чем больший разброс имеют разности … к чему мы и стремились.
Фактически в данном методе использована та же идея, что и при вычислении расстояния между точками, только примененная иным способом.
И с математической точки зрения использование квадратов и квадратных корней дает больше пользы, чем мы могли бы получить на основании абсолютных значений отклонений, благодаря чему среднеквадратическое отклонение применимо и для других математических задач.
О том, как найти среднеквадратическое отклонение, вам рассказал , Сергей Валерьевич
Среди множества показателей, которые применяются в статистике, нужно выделить расчет дисперсии. Следует отметить, что выполнение вручную данного вычисления – довольно утомительное занятие. К счастью, в приложении Excel имеются функции, позволяющие автоматизировать процедуру расчета. Выясним алгоритм работы с этими инструментами.
Дисперсия – это показатель вариации, который представляет собой средний квадрат отклонений от математического ожидания. Таким образом, он выражает разброс чисел относительно среднего значения. Вычисление дисперсии может проводиться как по генеральной совокупности, так и по выборочной.
Вычисление дисперсии может проводиться как по генеральной совокупности, так и по выборочной.
Способ 1: расчет по генеральной совокупности
Для расчета данного показателя в Excel по генеральной совокупности применяется функция ДИСП.Г . Синтаксис этого выражения имеет следующий вид:
ДИСП.Г(Число1;Число2;…)
Всего может быть применено от 1 до 255 аргументов. В качестве аргументов могут выступать, как числовые значения, так и ссылки на ячейки, в которых они содержатся.
Посмотрим, как вычислить это значение для диапазона с числовыми данными.
Способ 2: расчет по выборке
В отличие от вычисления значения по генеральной совокупности, в расчете по выборке в знаменателе указывается не общее количество чисел, а на одно меньше. Это делается в целях коррекции погрешности. Эксель учитывает данный нюанс в специальной функции, которая предназначена для данного вида вычисления – ДИСП.В. Её синтаксис представлен следующей формулой:
ДИСП. В(Число1;Число2;…)
В(Число1;Число2;…)
Количество аргументов, как и в предыдущей функции, тоже может колебаться от 1 до 255.
Как видим, программа Эксель способна в значительной мере облегчить расчет дисперсии. Эта статистическая величина может быть рассчитана приложением, как по генеральной совокупности, так и по выборке. При этом все действия пользователя фактически сводятся только к указанию диапазона обрабатываемых чисел, а основную работу Excel делает сам. Безусловно, это сэкономит значительное количество времени пользователей.
Функция стандартное отклонение это уже из разряда высшей математики относящейся к статистики. В Excel существует несколько вариантов использования Функции стандартного отклонения это:
- Функция СТАНДОТКЛОНП.
- Функция СТАНДОТКЛОН.
- Функция СТАНДОТКЛОНПА
Данные функции в статистике продаж нам понадобятся для выявления стабильности продаж (анализ XYZ). Эти данные можно использовать как для ценообразования, так и для формирования (корректирования) ассортиментной матрицы и для других полезных анализов продаж, о которых я обязательно расскажу в следующих статьях.
Предисловие
Давайте посмотрим на формулы сначала математическим языком, а после (ниже по тексту) подробно разберем формулу в Excel и как получившийся результат применяется в анализе статистических данных продаж.
Итак, Стандартное отклонение — это оценка среднеквадратического отклонения случайной величины x относительно её математического ожидания на основе несмещённой оценки её дисперсии)))) Не пугайтесь не понятных слов, потерпите и Вы все поймете!
Описание формулы: Среднеквадратическое отклонение измеряется в единицах измерения самой случайной величины и используется при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами. Определяется как квадратный корень из дисперсии случайной величины
Теперь стандартное отклонение — оценка среднеквадратического отклонения случайной величины x относительно её математического ожидания на основе несмещённой оценки её дисперсии:
Дисперсия;
— i -й элемент выборки;
Объём выборки;
Среднее арифметическое выборки:
Следует отметить, что обе оценки являются смещёнными. В общем случае несмещённую оценку построить невозможно. Однако оценка на основе оценки несмещённой дисперсии является состоятельной.
В общем случае несмещённую оценку построить невозможно. Однако оценка на основе оценки несмещённой дисперсии является состоятельной.
Правило трёх сигм () — практически все значения нормально распределённой случайной величины лежат в интервале . Более строго — приблизительно с 0,9973 вероятностью значение нормально распределённой случайной величины лежит в указанном интервале (при условии, что величина истинная, а не полученная в результате обработки выборки). Мы же будем использовать округленный интервал 0,1
Если же истинная величина неизвестна, то следует пользоваться не , а s . Таким образом, правило трёх сигм преобразуется в правило трёх s . Именно это правило поможет нам определить стабильность продаж, но об этом чуть позже…
Теперь Функция стандартного отклонения в Excel
Надеюсь я не слишком Вас загрузил математикой? Возможно кому то данная информация потребуется для реферата или еще каких-нибудь целей. Теперь разжуем как эти формулы работают в Excel. ..
..
Для определения стабильности продаж нам не потребуется вникать во все варианты функций стандартного отклонения. Мы будем пользоваться всего одной:
Функция СТАНДОТКЛОНП
СТАНДОТКЛОНП (число1 ;число2 ;… )
Число1, число2,.. — от 1 до 30 числовых аргументов, соответствующих генеральной совокупности.
Теперь разберем на примере:
Давайте создадим книгу и импровизированную таблицу. Данный пример в Excel Вы скачаете в конце статьи.
Продолжение следует!!!
И снова здравствуйте. Ну что!? Выдалась свободная минутка. Давайте продолжим?
И так стабильность продаж при помощи Функции СТАНДОТКЛОНП
Для наглядности возьмем несколько импровизированных товаров:
В аналитике, будь то прогноз, исследование или еще что то, что связано с статистикой всегда необходимо брать три периода. Это может быть неделя, месяц, квартал или год. Можно и даже лучше всего брать как можно больше периодов, но не менее трех.
Я специально показал утрированные продажи, где не вооруженным глазом видно, что продается стабильно, а что нет. Так проще будет понять как работают формулы.
И так у нас есть продажи, теперь нам нужно рассчитать средние значения продаж по периодам.
Формула среднего значения СРЗНАЧ(данные периода) в моем случае формула выглядит вот так =СРЗНАЧ(C6:E6)
Протягиваем формулу по всем товарам. Это можно сделать взявшись за правый угол выделенной ячейки и протянуть до конца списка. Или поставить курсор на столбец с товаром и нажать следующие комбинации клавиш:
Ctrl + Вниз курсор переместиться в коней списка.
Ctrl + Вправо, курсор переместиться в правую часть таблицы. Еще раз вправо и мы попадем на столбец с формулой.
Теперь зажимаем
Ctrl + Shift и нажимаем вверх. Так мы выделим область протягивания формулы.
И комбинация клавиш Ctrl + D протянет функцию там где нам надо.
Запомните эти комбинации, они реально увеличивают Вашу скорость работы в Excel, особенно когда Вы работаете с большими массивами.
Следующий этап, сама функция стандартного откланения, как я уже говорил мы будем пользоваться всего одной СТАНДОТКЛОНП
Прописываем функцию и в значениях функции ставим значения продаж каждого периода. Если у Вас продажи в таблице друг за другом можно использовать диапазон, как у меня в формуле =СТАНДОТКЛОНП(C6:E6) или через точку с запятой перечисляем нужные ячейки =СТАНДОТКЛОНП(C6;D6;E6)
Вот все расчеты и готовы. Но как понять, что продается стабильно, а что нет? Просто проставим условность XYZ где,
Х — это стабильно
Y — с не большими отклонениями
Z — не стабильно
Для этого используем интервалы погрешности. если колебания происходят в пределах 10% будем считать что продажи стабильны.
Если в пределах от 10 до 25 процентов — это будет Y.
И если значения вариации превышает 25% — это не стабильность.
Что бы правильно задать буквы каждому товару, воспользуемся формулой ЕСЛИ подробнее про . В моей таблице данная функция будет выглядеть так:
ЕСЛИ(H6
Соответственно все формулы протягиваем по всем наименованиям.
Постараюсь сразу ответить на вопрос, Почему интервалы 10% и 25%?
На самом деле интервалы могут быть иными, все зависит от конкретной задачи. Я специально показал Вам утрированные значения продаж, где разница видна на «глаз». Очевидно, что товар 1 продается не стабильно, но динамика показывает увеличение продаж. Такой товар оставляем в покое…
А вот товар 2, тут уже дистабилизация на лицо. И наши расчеты показывают Z, что говорит нам о не стабильности продаж. Товар 3 и Товар 5 показывают стабильные показатели, обратите внимание, Вариация в пределах 10%.
Т.е. Товар 5 с показателями 45, 46 и 45 показывает вариацию 1%, что является стабильным числовым рядом.
А вот Товар 2 с показателями 10, 50 и 5 показывают вариацию в 93%, что является НЕ стабильным числовым рядом.
После всех расчетов, можно поставить фильтр и отфильтровать стабильность, таким образом если Ваша таблица составляет несколько тысяч наименований вы с легкостью выделите которые не стабильны в продажах или же на оборот, какие стабильны.
В моей таблице не получилось «Y», я думаю для наглядности числового ряда, его нужно добавить. Пририсую Товар 6…
Вот видите, числовой ряд 40, 50 и 30 показывает 20% вариации. Вроде большой погрешности нет, но все же разброс существенный…
И так под итожим:
10,50,5 — Z не стабильность. Вариация более 25%
40,50,30 — Y на этот товар можно обратить внимание, и улучшить его продажи. Вариация меньше 25%, но больше 10%
45,46,45 — X это стабильность, с этим товаром пока ничего делать не надо. Вариация меньше 10%
На этом все! Надеюсь я все понятно изложил, если нет спрашивайте что не понятно. И буду благодарен Вам за каждый комментарий будь то похвала или критика. Так я буду знать, что Вы меня читаете и Вам, что очень ВАЖНО, интересно. И соответственно будут появляться новые уроки.
Формула коэффициента вариации | Расчет с помощью шаблона Excel
Формула коэффициента вариации (содержание)
- Формула
- Примеры
В статистике коэффициент вариации, также называемый CV, является инструментом, который помогает нам определить, как точки данных в наборе данных распределяются вокруг среднего значения. По сути, сначала наносятся все точки данных, а затем используется коэффициент вариации для измерения дисперсии этих точек друг от друга и от среднего значения. Таким образом, это помогает нам понять данные, а также увидеть шаблон, который они формируют. Он рассчитывается как отношение стандартного отклонения набора данных к среднему значению. Чем выше коэффициент вариации, тем выше уровень разброса данных вокруг среднего значения. Точно так же, чем меньше значение коэффициента вариации, тем меньше дисперсия и тем точнее будут результаты. Даже если среднее значение двух рядов данных значительно отличается, коэффициент вариации очень полезен для сравнения степени вариации одного ряда данных с другим.
По сути, сначала наносятся все точки данных, а затем используется коэффициент вариации для измерения дисперсии этих точек друг от друга и от среднего значения. Таким образом, это помогает нам понять данные, а также увидеть шаблон, который они формируют. Он рассчитывается как отношение стандартного отклонения набора данных к среднему значению. Чем выше коэффициент вариации, тем выше уровень разброса данных вокруг среднего значения. Точно так же, чем меньше значение коэффициента вариации, тем меньше дисперсия и тем точнее будут результаты. Даже если среднее значение двух рядов данных значительно отличается, коэффициент вариации очень полезен для сравнения степени вариации одного ряда данных с другим.
Формула для коэффициента вариации:
Коэффициент вариации = стандартное отклонение / среднее значение
Шаги для расчета коэффициента вариации:
Шаг 1: Вычислите среднее значение набора данных. Среднее значение — это среднее значение всех значений, которое можно рассчитать, взяв сумму всех значений, а затем разделив ее на количество точек данных.
Шаг 2: Затем вычислите стандартное отклонение набора данных. Это немного трудоемкий процесс. Стандартное отклонение можно рассчитать как: √ [Σ(X i – X m ) 2 / (n – 1)] . X i — i-я точка данных, а X m — среднее значение набора данных. Кроме того, мы также можем найти стандартное отклонение в Excel, используя функцию STDEV.S().
Шаг 3: Разделите стандартное отклонение на среднее значение, чтобы получить коэффициент вариации.
Примеры формулы коэффициента вариации (с шаблоном Excel)Давайте рассмотрим пример, чтобы лучше понять расчет коэффициента вариации.
Вы можете скачать этот шаблон Excel формулы коэффициента вариации здесь — Формула коэффициента вариации Шаблон Excel
Формула коэффициента вариации — пример № 1
Допустим, у нас есть два набора данных, A и B, и каждый содержит 20 случайных точки данных. Рассчитайте коэффициент вариации для набора данных X и Y.
Рассчитайте коэффициент вариации для набора данных X и Y.
Решение:
Среднее значение рассчитывается как:
- Среднее значение набора данных A = 61,2
- Среднее значение набора данных B = 51,8
Теперь нам нужно рассчитать разницу между точками данных и средним значением.
Аналогичным образом рассчитайте все значения набора данных A.
Аналогично рассчитайте все значения набора данных B.
Рассчитайте квадрат разности для наборов данных A и B
Стандартное отклонение рассчитывается по приведенной ниже формуле
Стандартное отклонение = √ [Σ (X i – X m ) 2 / (n – 1)]
Коэффициент вариации рассчитывается по приведенной ниже формуле 0 0 0 0 9 0 9 0 вариации = стандартное отклонение / среднее значение
- Коэффициент вариации A = 22,982 / 61,2 = 0,38
- Коэффициент вариации B = 30,574 / 51,8 = 0,59
Итак, если вы видите здесь, B имеет более высокий коэффициент вариации, чем A, что означает, что точки данных B более разбросаны, чем A.
Формула коэффициента вариации – Пример №2
Допустим, вы очень не склонны к риску и хотите инвестировать деньги в фондовый рынок. Поскольку ваш аппетит к риску низок, вы хотите инвестировать в безопасные акции, которые имеют более низкое стандартное отклонение и коэффициент вариации. Вы выбрали 3 акции на основе их фундаментальной и технической информации и хотите выбрать 2 акции. Вы также собрали информацию об их исторической доходности за последние 15 лет.
Решение:
Среднее значение рассчитывается как:
Стандартное отклонение рассчитывается с использованием формулы Excel
Коэффициент вариации рассчитывается с использованием формулы, приведенной ниже
Коэффициент. / Среднее
- Коэффициент вариации ABC = 7,98% / 14% = 0,57
- Коэффициент вариации XYZ = 6,28 % / 90,1% = 0,69
- Коэффициент вариации QWE = 6,92% / 8,9% = 0,77
На основании этой информации вы выберете акции ABC и XYZ для инвестирования, так как они имеют самый низкий коэффициент вариации.
Пояснение
Поскольку коэффициент вариации является мерой риска, он помогает измерять волатильность цен на акции и другие финансовые инструменты. Это также помогает инвесторам и аналитикам сравнивать риски, связанные с различными потенциальными инвестициями.
Коэффициент вариации подобен стандартному отклонению, но стандартное отклонение двух переменных не может быть полезно для сравнения. Но использование стандартного отклонения и среднего значения делает относительное сравнение более содержательным. Существует также ограничение коэффициента вариации. Предположим, что среднее значение набора данных равно нулю. В этом случае этот инструмент станет неэффективным. Мало того, если у нас есть набор данных, который имеет много положительных и отрицательных значений, коэффициент вариации становится очень проблематичным. Таким образом, это только более полезно, когда наборы данных имеют одинаковый знак плюс-минус.
Актуальность и использование формулы коэффициента вариации
Коэффициент вариации имеет значение во многих других областях, помимо статистики. Например, в области финансов коэффициент вариации является мерой риска. Он похож на стандартное отклонение, поскольку оно также используется в качестве меры риска, но разница в том, что коэффициент вариации является лучшим индикатором относительного риска. Например, предположим, что ожидаемая доходность A составляет 15 %, а ожидаемая доходность B — 10 %, а стандартное отклонение A — 10 %, а стандартное отклонение B — 5 %. Чтобы выбрать лучшую инвестицию, можно использовать коэффициент вариации. Таким образом, коэффициент вариации А равен 10/15 = 0,666, а коэффициент вариации В равен 5/10 = 0,5. Таким образом, B — лучшая инвестиция, чем A.
Например, в области финансов коэффициент вариации является мерой риска. Он похож на стандартное отклонение, поскольку оно также используется в качестве меры риска, но разница в том, что коэффициент вариации является лучшим индикатором относительного риска. Например, предположим, что ожидаемая доходность A составляет 15 %, а ожидаемая доходность B — 10 %, а стандартное отклонение A — 10 %, а стандартное отклонение B — 5 %. Чтобы выбрать лучшую инвестицию, можно использовать коэффициент вариации. Таким образом, коэффициент вариации А равен 10/15 = 0,666, а коэффициент вариации В равен 5/10 = 0,5. Таким образом, B — лучшая инвестиция, чем A.
Рекомендуемые статьи
Это руководство по формуле коэффициента вариации. Здесь мы обсудим, как рассчитать коэффициент вариации, используя формулу, а также практические примеры и загружаемый шаблон Excel. Вы также можете прочитать следующие статьи, чтобы узнать больше:
- Что такое формула скорректированного R в квадрате?
- Примеры формулы определения коэффициента
- Как рассчитать коэффициент корреляции с помощью формулы?
- Формула ковариации с шаблоном Excel
Как рассчитать коэффициент дисперсии в Excel (3 метода)
В Excel пользователи вычисляют различные статистические свойства для демонстрации разброса данных. По этой причине пользователи пытаются рассчитать коэффициент дисперсии в Excel. Вычислить коэффициент дисперсии ( CV ) легко, используя Excel STDEV.P или STDEV. S со встроенными функциями, а также типичные Формулы статистики .
По этой причине пользователи пытаются рассчитать коэффициент дисперсии в Excel. Вычислить коэффициент дисперсии ( CV ) легко, используя Excel STDEV.P или STDEV. S со встроенными функциями, а также типичные Формулы статистики .
Допустим, у нас есть набор данных, рассматриваемый как Население ( Набор ) или Выборка , и мы хотим вычислить Коэффициент дисперсии ( CV ).
В этой статье мы демонстрируем типичную формулу Статистика , а также функции СТАНДОТКЛОН.П и СТАНДОТКЛОН.С для расчета коэффициента дисперсии в Excel.
Скачать книгу Excel
Что такое коэффициент дисперсии?
3 простых способа рассчитать коэффициент дисперсии в Excel
Метод 1: использование формулы статистики для расчета коэффициента дисперсии в Excel
Метод 2: вычисление коэффициента дисперсии (CV) с использованием функций STDEV. P и AVERAGE.
P и AVERAGE.
Метод 3: использование функций STDEV.S и AVERAGE для расчета коэффициента дисперсии
Вывод
Статьи по Теме
Загрузить книгу ExcelЧто такое коэффициент дисперсии?
Как правило, коэффициент дисперсии ( CV ) определяется как отношение между стандартным отклонением ( σ ) и средним или средним значением ( μ ). Он отображает степень изменчивости по сравнению со средним значением или средним значением совокупности (набор) или выборки . Итак, есть 2 различных формул для Коэффициент дисперсии ( CV ). Они:
🔺 Коэффициент дисперсии ( CV ) для населения или Набор ,
🔺 Коэффициент дисперсии ( CV ) для Образец ,
⏩ Здесь стандартное отклонение для населения ,
⏩ Стандартное отклонение для Образец ,
3 простых способа расчета коэффициента дисперсии в Excel
Если пользователи используют формулу статистики для расчета Коэффициента дисперсии ( CV ), им сначала необходимо найти стандартное отклонение для населения ( σ ) или выборка ( S) и Среднее или Среднее ( μ ). Кроме того, пользователи могут использовать STDEV.P и STDEV.S для расчета населения и Выборка вариантов расчета стандартного отклонения . Следуйте приведенному ниже разделу для подробного расчета.
Кроме того, пользователи могут использовать STDEV.P и STDEV.S для расчета населения и Выборка вариантов расчета стандартного отклонения . Следуйте приведенному ниже разделу для подробного расчета.
Способ 1. Использование формулы статистики для расчета коэффициента дисперсии в Excel
Перед расчетом коэффициента дисперсии ( CV ) пользователям необходимо настроить данные для поиска компонентов формулы. Как мы упоминали ранее, Статистическая формула для Коэффициента дисперсии ( CV ) равна
Коэффициент дисперсии для населения ,
или
Коэффициент дисперсии для образца ,
🔄 Настройка данных
Пользователям необходимо вручную найти компоненты формулы Коэффициент дисперсии ( CV ), такие как 9Чтобы вычислить коэффициент Дисперсия ( CV ).
⏩ Расчетное среднее (мк)
Первым этапом вычисления Коэффициента дисперсии является вычисление Среднего данных. Используйте функцию СРЗНАЧ для расчета Среднее значение или Среднее значение данного набора данных. Используйте приведенную ниже формулу в любой ячейке (например, C14 ).
=СРЕДНЕЕ(C5:C13)
⏩ Нахождение отклонения (x i -μ)
После этого пользователи должны найти Отклонение от среднего ( x i -μ) . Это минус значение каждой записи ( x i ) до значения Mean ( μ) . Введите приведенную ниже формулу в поле 9.0005 Отклонение (т.е. Колонка D ) ячеек.
=C5-$C$14
⏩ Нахождение суммы квадратов отклонений ∑(xi-μ) 2
Теперь, Возведите в квадрат значения отклонения (xi-μ) 2 и поместите данные в соседние ячейки (т. е. Столбец E ). Затем суммируйте квадраты значений в ячейке E14 . Просто используйте функцию SUM в E14 ячейка, чтобы найти сумму квадратов отклонений.
е. Столбец E ). Затем суммируйте квадраты значений в ячейке E14 . Просто используйте функцию SUM в E14 ячейка, чтобы найти сумму квадратов отклонений.
=СУММ(Е5:Е13)
Функция СУММ предоставляет общее значение Column E .
⏩ Расчет стандартного отклонения (σ или S )
Стандартное отклонение для населения ( σ ) имеет свою собственную формулу как
Стандартное отклонение для населения ( набор ),
Таким образом, для расчета стандартного отклонения необходимо использовать формулу, применяемую в ячейке G6 .
➤ Вставьте приведенную ниже формулу в ячейку G6 , чтобы найти стандартное отклонение ( σ ).
=КОРЕНЬ(E14/СЧЕТ(C5:C13))
Функция SQRT возвращает значение квадратного корня и Функция COUNT возвращает общее количество записей.
➤ Нажмите или нажмите . Введите , чтобы применить формулу, и значение стандартного отклонения появится в ячейке G6 .
Опять же, используйте версию Sample формулы Standard Deviation , чтобы найти Standard Deviation . Формула,
Стандартное отклонение для Образец ,
➤ Введите следующую формулу в ячейку H6 для отображения стандартного отклонения .
=КОРЕНЬ(E14/(СЧЕТ(C5:C13)-1))
➤ Используйте клавишу Введите , чтобы применить формулу в ячейке H6 .
⏩ Расчет коэффициента дисперсии (CV)
После нахождения всех необходимых компонентов, таких как Стандартное отклонение и Среднее , разделите эти двухкомпонентные ( Стандартное отклонение/Среднее ) на предварительно отформатированную ячейку Процент .
➤ Выполните следующую формулу в ячейке G11 , чтобы найти коэффициент дисперсии для населения ( Set ).
=G6/C14
➤ Нажмите клавишу Enter , чтобы применить приведенную ниже формулу в ячейке h21 , чтобы найти Коэффициент дисперсии для выборки .
=H6/C14
🔺 Наконец, коэффициент дисперсии для обоих вариантов отображается в ячейках G11 и h21 , как вы можете видеть на скриншоте ниже.
Подробнее: Как выполнить анализ отклонений в Excel (с быстрыми шагами)
Аналогичные показания
- Как рассчитать объединенную дисперсию в Excel (с помощью простых шагов)
- Расчет дисперсии портфеля в Excel (3 интеллектуальных подхода)
- Как рассчитать процент отклонения в Excel (3 простых метода)
Метод 2: Расчет коэффициента дисперсии (CV) с использованием функций STDEV.P и AVERAGE
Excel предлагает несколько встроенных функций для выполнения различных статистических данных расчеты. Функция STDEV.P является одной из них. В качестве аргументов он принимает числа.
Функция STDEV.P является одной из них. В качестве аргументов он принимает числа.
Как мы упоминали ранее, коэффициент дисперсии ( CV ) является частным двух компонентов (т. е. стандартного отклонения ( σ ) и среднего ( μ )). Функция СТАНДОТКЛОН.P находит стандартное отклонение ( σ ) для населения , а функция СРЕДНЕЕ приводит к результату Среднее ( μ ) или Среднее .
Шаг 1: Используйте следующую формулу в ячейке E6 .
=СТАНДОТКЛОН.P(C5:C13)/СРЕДНИЙ(C5:C13)
Функция СТАНДОТКЛОН.P возвращает стандартное отклонение для совокупности, а функция СРЗНАЧ возвращает среднее или среднее значение.
Шаг 2: Нажмите клавишу Enter , чтобы применить формулу. Мгновенно Excel отображает Коэффициент дисперсии ( CV ) в предварительно отформатированной ячейке Процент .
Подробнее: Как рассчитать дисперсию в Excel (Краткое руководство)
Метод 3: Использование функций STDEV.S и AVERAGE для Расчет коэффициента дисперсии
В качестве альтернативы функции СТАНДОТКЛОН.P в Excel имеется СТАНДОТКЛОН.С для выборочных данных для расчета стандартного отклонения ( σ ). Подобно функции СТАНДОТКЛОН.P , функция СТАНДОТКЛОН.S принимает в качестве аргументов числа. Типичная формула коэффициента отклонения ( CV ) представляет собой отношение между стандартным отклонением ( σ ) и средним значением ( μ ).
Шаг 1: Используйте следующую формулу в ячейке E6 .
=СТАНДОТКЛОН.С(C5:C13)/СРЗНАЧ(C5:C13)
Шаг 2: Теперь используйте клавишу Enter для отображения коэффициента отклонения в ячейке E6 .
Подробнее: Как рассчитать дисперсию с помощью сводной таблицы в Excel (с помощью простых шагов)
Заключение
В этой статье мы демонстрируем типичный способ статистики вместе с функциями для расчета коэффициента дисперсии в Excel. Пользователи могут выбрать любой из методов расчета Коэффициент дисперсии как им заблагорассудится. Надеюсь, что эта статья прояснит ваше понимание коэффициента дисперсии и его расчета. Комментируйте, если у вас есть дополнительные вопросы или есть что добавить.
Связанные статьи
- Как рассчитать отклонение бюджета в Excel (с помощью быстрых шагов)
- Формула бюджетного и фактического отклонения в Excel (с примером)
- Расчет выборочной дисперсии в Excel (2 эффективных подхода)
- Как рассчитать процентное отклонение между двумя числами в Excel
Меры изменчивости | Real Statistics Using Excel
We consider a random variable x and a data set S = { x 1 , x 2 , …, x n } of size n , который содержит возможные значения x . Набор данных может представлять либо изучаемую популяцию, либо выборку, взятую из популяции. Среднее – это статистика, которая чаще всего используется для характеристики центра данных в С . Теперь мы рассмотрим следующие обычно используемые меры изменчивости данных вокруг среднего, а именно стандартное отклонение , дисперсию , квадратное отклонение и среднее абсолютное отклонение .
Кроме того, мы также исследуем три другие меры изменчивости, которые не связаны со средним значением, а именно среднее абсолютное отклонение , диапазон и межквартильный диапазон .
Из этих статистических данных чаще всего используются дисперсия и стандартное отклонение.
Функции Excel : Если R является диапазоном Excel, который содержит элементы данных в S , то функция Excel, которая вычисляет каждую из этих статистических данных, показана на рисунке 1. Функции, отмеченные звездочкой, являются дополнительными функциями, найденными в Real Пакет ресурсов статистики, хотя эквивалентные формулы в стандартном Excel описаны позже.
| Статистика | Excel 2007 | Excel 2010+ | Символ |
| Дисперсия населения | ВАРП(р) | ВАР. П(Р) П(Р) | о 2 |
| Выборочная дисперсия | ВАР(Р) | ВАР.С(Р) | с 2 |
| Стандартное отклонение населения | СТАНДАРТ(R) | СТАНДОТКЛОН.П(Р) | о |
| Стандартное отклонение выборки | СТАНДОТКЛОН(R) | СТАНДОТКЛОН.S(R) | с |
| Квадрат отклонения | DEVSQ(R) | DEVSQ(R) | нержавеющая сталь |
| Среднее абсолютное отклонение | АВЕДЕВ(Р) | АВЕДЕВ(Р) | ААД |
| Среднее абсолютное отклонение | СРЕДНЕЕ(Р) * | СРЕДНЕЕ(Р) * | БЕЗ |
| Диапазон | РНГ(R) * | РНГ(R) * | |
| Межквартильный диапазон | IQR(R, б ) * | IQR(R, б ) * | ИКР |
| Коэффициент вариации | СТАНДОТКЛОН(R)/СРЕДНИЙ(R) | СТАНДОТКЛОН.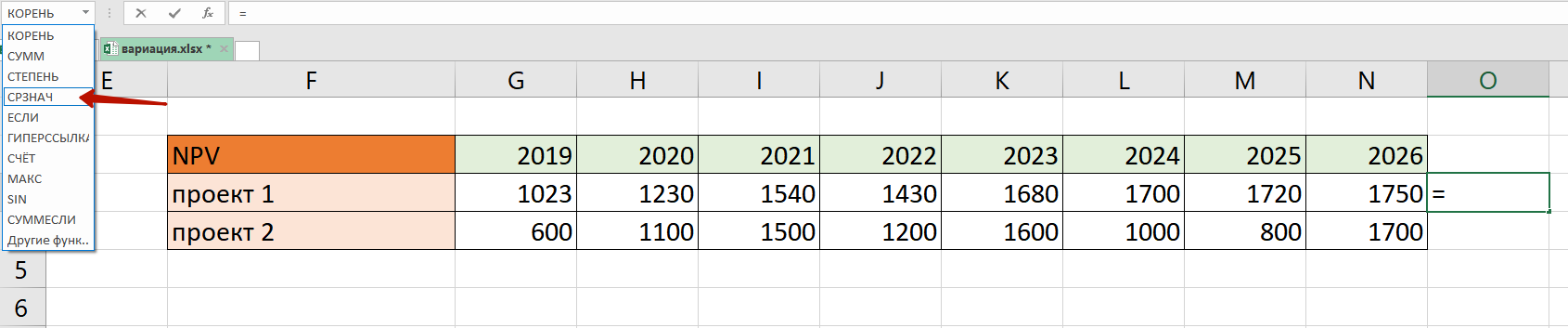 С(R)/СРЕДНИЙ(R) С(R)/СРЕДНИЙ(R) | В |
Рисунок 1 – Показатели изменчивости
Наблюдение : эти функции игнорируют любые пустые или нечисловые ячейки.
Дисперсия
Определение 1 : Дисперсия является мерой разброса данных вокруг среднего значения. Где S представляет собой популяцию дисперсии населения (символ σ 2 ) рассчитывается из среднего значения µ следующим образом:
, где s . (символ с 2 ) вычисляется из выборочного среднего x̄ следующим образом:
Причина, по которой выражение для дисперсии совокупности включает деление на n , в то время как дисперсия выборки включает деление на n – 1, объясняется в свойстве 3 Оценщиков, где для получения несмещенной оценки дисперсии населения требуется деление на n – 1.
Функция Excel : Выборочная дисперсия рассчитывается в Excel с использованием функции рабочего листа ВАР . Дисперсия населения рассчитывается в Excel с помощью функции VARP . В Excel 2010/2013 альтернативными формами этих функций являются VAR.S и VAR.P .
Пример 1 : если S = {2, 5, -1, 3, 4, 5, 0, 2} представляет совокупность, то дисперсия = 4,25.
Рассчитывается следующим образом. Во-первых, среднее значение = (2+5-1+3+4+5+0+2)/8 = 2,5, поэтому квадрат отклонения SS = (2–2,5) 2 + (5–2,5) 2 + (-1–2,5) 2 + (3–2,5) 2 + (4–2,5) 2 + (5–2,5) 6 7 + 900 –2,5) 2 + (2–2,5) 2 = 34. Таким образом, дисперсия = SS / n = 34/8 = 4,25
Если вместо S представляет выборку, то среднее по-прежнему 2,5, но дисперсия = SS / ( n– 1) = 34/7 = 4,86.
Их можно рассчитать в Excel по формулам VARP(B3;B10) и VAR(B3:B10), как показано на рисунке 2.
Рисунок 2 – Примеры показателей изменчивости
Наблюдение : когда данные представлены в виде таблиц частот, полезны следующие свойства. Нажмите здесь, чтобы просмотреть доказательства этих свойств.
Свойство 1 : если x̄ является средним значением образца S = { x 1 , x 2 ,…, x N 333333333 3 2 ,…, x N 33333333 3 2 . можно выразить через
Собственность 2 : если µ является средним значением популяции S = { x 1 , x 2 ,… x 2 ,… x 2 ,… x . дисперсия совокупности может быть выражена как
Определение 2 : Стандартное отклонение – это квадратный корень из дисперсии. Таким образом, стандартные отклонения населения и выборки рассчитываются соответственно следующим образом:
Таким образом, стандартные отклонения населения и выборки рассчитываются соответственно следующим образом:
Функция Excel : Стандартное отклонение выборки рассчитывается в Excel с использованием функции рабочего листа СТАНДОТКЛОН . Стандартное отклонение генеральной совокупности рассчитывается в Excel с помощью функции STDEVP . В Excel 2010/2013 альтернативными формами этих функций являются СТАНДОТКЛОН.S и СТАНДОТКЛОН.P .
Пример 2 : Если S = {2, 5, -1, 3, 4, 5, 0, 2} является совокупностью, то стандартное отклонение = квадратный корень из дисперсии совокупности = = 2,06
Если S является выборкой, то стандартное отклонение выборки = квадратный корень выборочной дисперсии = = 2,20
Это результаты формул СТАНДОТКЛОН(B3:B10) и СТАНДОТКЛОН(B3:B10), как показано на рисунке 2.
Функции реальной статистики : Ресурсный пакет реальной статистики предоставляет следующие функции массива:
VARCOL (R1) = диапазон строк, который содержит образцы стандартных отклонений каждого из столбцов в R1
STDEVCOL (R1) = диапазон строк, который содержит выборочные стандартные отклонения каждого из столбцов в R1
VARROW (R1) = диапазон столбцов, который содержит выборочные стандартные отклонения каждой из строк в R1
STDEVROW (R1) = диапазон столбцов, который содержит выборочные стандартные отклонения каждой из строк в R1
Пример 3 диапазон L4:N11 на рисунке 3.
Формула =VARCOL(J4:L11) дает первый результат (в диапазоне J15:L15), а формула =STDEVCOL(J4:L11) дает второй результат (в диапазоне J16:L16). Помните, что после ввода любой из этих формул вы должны нажать Ctrl-Shft-Enter .
Рисунок 3 — Дисперсия выборки и стандартное отклонение по столбцу
Свойство 3 : Если популяция { x 1 , x 2 ,…, x N 2 ,…, x N 2 , ,…, x N 2 , ,…, x N 20933} имеет среднее значение µ x и стандартное отклонение σ x и популяция {y 1 , Y 2 ,…, Y M 9933333,…, y M 333, y M 93333333333. has a a a a . and standard deviation σ y , then the variance of the combined population is
Thus if µ x = µ y the combined population variance would be
Свойство 4 : Если образец { x 1 , x 2 ,…, x N } имеет среднее значение x и стандартный Deviation S 333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333. Y 1 , Y 2 ,…, Y M } имеет среднее значение ȳ , а стандартное отклонение S Y , затем дискавация комбинированной выборки —
Y 1 , Y 2 ,…, Y M } имеет среднее значение ȳ , а стандартное отклонение S Y , затем дискавация комбинированной выборки —
Таким = ȳ , комбинированная выборочная дисперсия будет равна
Пример 4 : Найдите среднее значение и дисперсию выборки, полученной в результате объединения двух выборок {3, 4, 6, 7} и {6, 1, 5}.
Рисунок 4 – Расчет комбинированного среднего значения и стандартного отклонения
Данные двух выборок представлены в диапазоне B3:C7 на рисунке 4. Из них вычисляются среднее значение, дисперсия и стандартное отклонение для каждой двух образцов (диапазоны B12:B15 и C12:C15). Используя свойство 4, мы можем вычислить среднее значение и дисперсию комбинированной выборки (D13 и D14).
Если мы просто объединим две выборки, мы получим данные в диапазоне F3:F10, из которых мы можем вычислить среднее значение, дисперсию и стандартное отклонение обычным способом (диапазон D12:D18). Как мы видим, результаты совпадают.
Как мы видим, результаты совпадают.
Наблюдение : На практике вместо использования свойств 3 и 4 мы используем подход, показанный в следующем примере, тем более что его можно применять к более чем двум выборкам или совокупностям.
Пример 5 : Найдите среднее значение и дисперсию выборки, полученной в результате объединения трех выборок, показанных в диапазоне A3:D6 на рисунке 5.
Рисунок 5 – Расчет комбинированного среднего значения и дисперсии
У нас есть три выборки, общий объем выборки которых равен 58 (ячейка B7), рассчитанный с помощью =СУММ(B4:B6). Сумма элементов в каждом образце может быть рассчитана по среднему значению, как показано в диапазоне F4:F6. Например. сумма всех элементов данных в выборке 1 равна 276 (ячейка F4), рассчитанная по формуле =B4*C4. Таким образом, сумма всех элементов во всех трех образцах равна 786 (ячейка F7), рассчитанная по формуле =СУММ(F4:F6). Таким образом, среднее значение объединенной выборки составляет 13,5517 (ячейка C7), рассчитанное по формуле =F7/B7. 92)/(B7-1), основанный на свойстве 1. Таким образом, стандартное отклонение равно 12,6909.
92)/(B7-1), основанный на свойстве 1. Таким образом, стандартное отклонение равно 12,6909.
Квадратное отклонение
Определение 3 : Квадратное отклонение (символ SS для суммы квадратов ) наиболее часто используется в тестах ANO 90.0VA0 Он рассчитывается как
Функция Excel : Квадрат отклонения рассчитывается в Excel с использованием функции рабочего листа DEVSQ .
Пример 6 : Если S = {2, 5, -1, 3, 4, 5, 0, 2}, квадрат отклонения = 34. Это то же самое, что и результат формулы DEVSQ(B3 : B10) Как показано на рисунке 2.
Среднее абсолютное отклонение
Определение 4 : Среднее абсолютное отклонение ( AAD ) Набор данных S рассчитывается как
 Функция Excel
Функция Excel
Пример 7 : Если S = {2, 5, -1, 3, 4, 5, 0, 2}, среднее абсолютное отклонение = 1,75. Это то же самое, что и результат формулы AVEDEV(B3:B10), как показано на рисунке 2.
Медианное абсолютное отклонение
Определение 5 : Медианное абсолютное отклонение ( MAD ) набора данных S рассчитывается как
Медиана {| x i – | : x я в S }
где = медиана элементов данных в S .
Формула Excel : Если R представляет собой диапазон, содержащий элементы данных в S , то MAD S можно рассчитать в Excel по формуле массива:
=MEDIAN(ABS(R-MEDIAN(R )))
Несмотря на то, что значение представлено в одной ячейке, необходимо нажать Ctrl-Shft-Enter , чтобы получить значение массива, иначе результат будет неверным. Эта функция работает правильно только тогда, когда R не содержит пустой ячейки или ячейки с нечисловым значением.
Эта функция работает правильно только тогда, когда R не содержит пустой ячейки или ячейки с нечисловым значением.
В качестве альтернативы вы можете использовать функцию MAD (R), которая содержится в пакете ресурсов Real Statistics. Эта функция работает правильно, даже если R содержит пустые ячейки и/или ячейки с нечисловыми значениями. Вам не нужно нажимать Ctrl-Shft-Enter , чтобы использовать эту функцию.
Пример 8 : Если S = {2, 5, -1, 3, 4, 5, 0, 2}, среднее абсолютное отклонение = 2, поскольку S = {-1, 0, 2, 2, 3, 4, 5, 5} и, следовательно, медиана S = (2+3)/2 = 2,5. Таким образом, MAD = медиана {3,5, 2,5, 0,5, 0,5, 0,5, 1,5, 2,5, 2,5} = {0,5, 0,5, 0,5, 1,5, 2,5, 2,5, 2,5, 3,5}, то есть (1,5+2,5)/2 = 2.
Вы можете получить тот же результат, используя формулу =MAD(E3:E10), как показано на рисунке 2.
Наблюдение : на этот показатель меньше влияют крайние значения в хвостах, поскольку данные в хвостах меньшее влияние на расчет медианы, чем на среднее.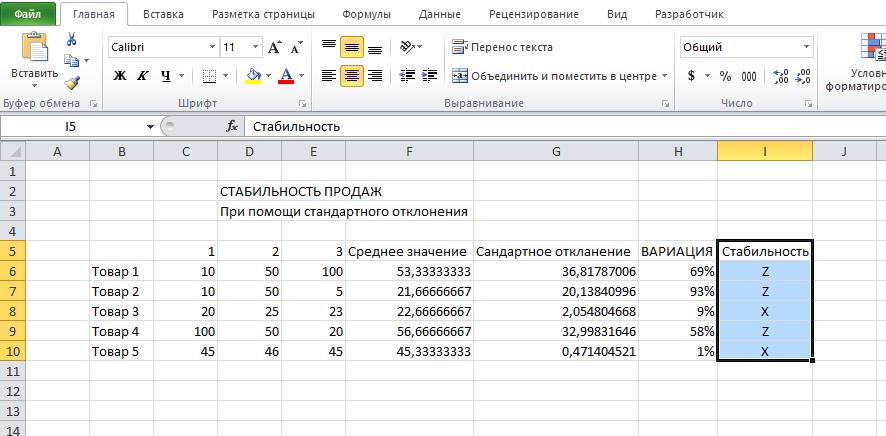
Диапазон
Определение 6 : Диапазон набора данных S является грубой мерой изменчивости и состоит просто из разницы между наибольшим и наименьшим значениями в S .
Формула Excel : Если R является диапазоном, который содержит элементы данных в S , то диапазон S можно рассчитать в Excel по формуле:
=MAX(R) – MIN(R)
В качестве альтернативы вы можете использовать функцию RNG (R), которая содержится в пакете ресурсов Real Statistics.
Пример 9 : Если S = {2, 5, -1, 3, 4, 5, 0, 2}, диапазон = 5 – (-1) = 6. Вы можете получить тот же результат, используя формула =RNG(E3:E10), как показано на рисунке 2.
Межквартильный диапазон
Определение 7 рассчитывается как 75% процентиль S минус 25% процентиль. IQR обеспечивает грубую аппроксимацию изменчивости вблизи центра данных в S.
Формула Excel : если R представляет собой диапазон, содержащий элементы данных в S , то IQR S можно рассчитать в Excel по формуле:
= КВАРТИЛЬ (R, 3) – QUARTILE(R, 1)
Начиная с Excel 2010 существует еще одна версия функции квартиля, которая называется QUARTILE.EXC. Таким образом, альтернативной версией IQR является
=QUARTILE.EXC(R, 3) – QUARTILE.EXC(R, 1)
Дополнительные сведения о функциях QUARTILE и QUARTILE.EXC см. в разделе Функции ранжирования в Excel. Кроме того, вы можете рассчитать межквартильный диапазон с помощью функции IQR (R, b ), который содержится в пакете ресурсов Real Statistics. Когда b = FALSE (по умолчанию), возвращается первая версия IQR, а когда b = TRUE, возвращается вторая версия.
Пример 10 : Если S = {2, 5, -1, 3, 4, 5, 0, 2}, то первая версия IQR = 4,25 – 1,5 = 2,75, а вторая версия IQR = 4,75 – 0,5 = 4,25. Вы можете получить тот же результат, используя формулы реальной статистики =IQR(B3:B10) и =IQR(B3:B10,TRUE), как показано на рис.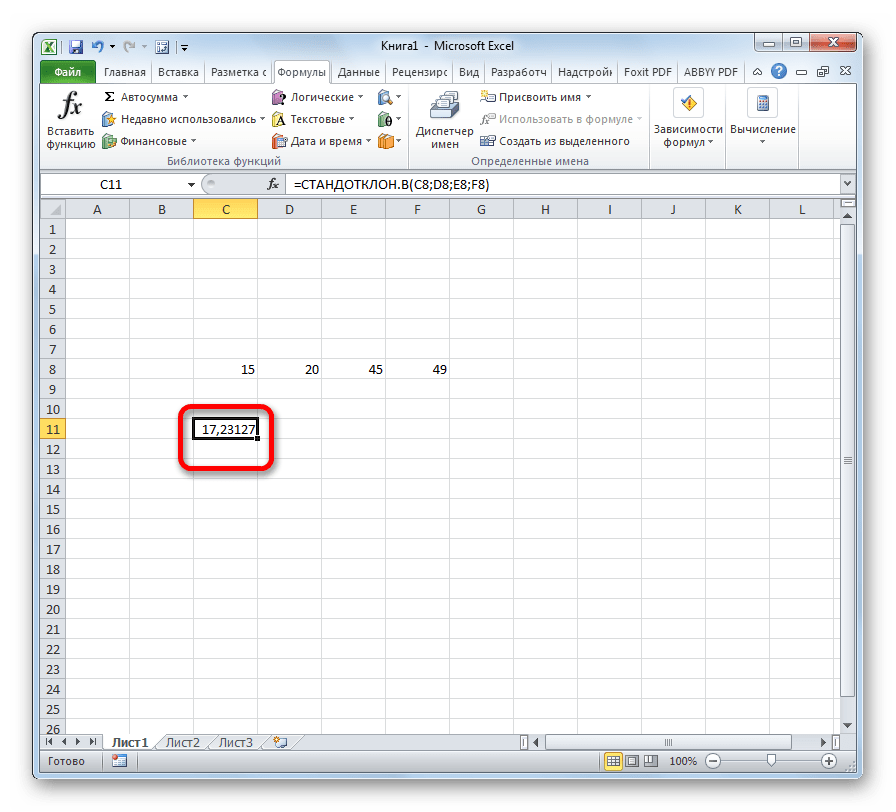 2.
2.
Наблюдение : Дисперсия, стандартное отклонение, среднее абсолютное отклонение и срединное абсолютное отклонение измеряют как изменчивость вблизи центра, так и изменчивость хвостов распределения, которое представляет данные. Среднее абсолютное отклонение и среднее абсолютное отклонение не придают чрезмерного веса хвостам. С другой стороны, диапазон использует только две крайние точки, а межквартильный диапазон использует только среднюю часть данных.
Коэффициент вариации
Определение 8 : Коэффициент вариации (он же коэффициент изменчивости ), V (OR CV ), из Data S. S. 9093 S. рассчитывается как
V = s/x̄
Поскольку s и x̄ имеют одинаковые единицы измерения, V не имеет единиц измерения. Эта статистика имеет смысл только для данных шкалы отношений. Чем выше значение V тем более дисперсия есть.
Очевидно, что коэффициент вариации определяется только тогда, когда среднее значение не равно нулю.
Формула Excel : если R представляет собой диапазон, содержащий элементы данных в S , то коэффициент вариации для S можно рассчитать в Excel по формуле:
=STDEV.S(R)/AVERAGE (R)
Версия популяции V равна σ/μ , что можно рассчитать в Excel по формуле
=STDEV.P(R)/AVERAGE(R)
Пример 11 : Если S = {2, 5, -1, 3, 4, 5, 0, 2} представляет выборку, то как видно из примера 1, коэффициент вариации равен
V = s/x̄ = 2,203892/2,5 = 88,16%
9%, а акция B имеет ожидаемую доходность 8% со стандартным отклонением 5%. Используйте коэффициент вариации, чтобы определить, какие инвестиции лучше.
Поскольку V A = 0,09/0,12 = 0,75 и V B = 0,05/08 = 0,625, акции B считаются лучшими инвестициями, поскольку их относительный риск (равный к его коэффициенту вариации) ниже.
Определение, формула, интерпретация, примеры и часто задаваемые вопросы
Коэффициент вариации — важная концепция, позволяющая прогнозировать переменные в наборах данных и за их пределами. Хотя он уходит своими корнями в математику и статистику, коэффициент вариации может применяться в различных контекстах, включая исследования населения и инвестиции на фондовом рынке.
Так как же работает коэффициент вариации в качестве статистической меры? Чтобы ответить на этот вопрос, давайте рассмотрим его различные части, включая определение, примеры расчетов и другие связанные понятия.
Что такое коэффициент вариации?Коэффициент вариации, также известный как относительное стандартное отклонение, представляет собой статистическую концепцию, учитывающую относительную изменчивость наборов данных. В частности, он указывает размер стандартного отклонения от его среднего значения.
В обзорных исследованиях коэффициент вариации позволяет сравнивать вариабельность внутри существенно разных групп; то есть результаты двух систематических исследований, которые не имеют одинаковых параметров классификации или мер ценности.
Например, если коэффициент вариации исследования А составляет 14 %, а коэффициент вариации исследования Б — 20 %, можно сказать, что исследование В имеет более высокую степень вариации по сравнению со своим средним значением.
Как рассчитать коэффициент вариации в опросеСтандартная формула для расчета коэффициента вариации выглядит следующим образом:
Коэффициент вариации (CV) = (стандартное отклонение/среднее значение) × 100.
В зависимости от контекста приложения вы можете внести небольшие изменения в эта формула. Например, если вы хотите рассчитать CV в финансовых исследованиях, вы можете переписать формулу следующим образом:
Коэффициент вариации = (Волатильность ÷ Ожидаемая доходность) × 100%
Давайте посмотрим, как применить эту формулу в опросных исследованиях.
Организация проводит исследования рынка в разных группах и представляет следующие результаты:
Читать: Корреляционные исследования: типы, примеры и методы
Целевая аудитория A
Отклонение: 10
Целевая аудитория B
Среднее значение: 50
Стандартное отклонение: 7,5
Чтобы выбрать более подходящий рынок для инвестиций, они могут сравнить коэффициент вариации обоих вариантов.
Коэффициент вариации (A) = (60÷10) × 100% = 600%
Коэффициент вариации (B) = (50÷7,5) × 100% = 667%
На основании этого результата организация принимает решение инвестировать в целевую аудиторию А, потому что она предлагает более низкий коэффициент вариации.
Варианты использования/промышленные применения коэффициента вариации Приложение 1Читать: 7 Типы шкал измерения данных в исследованиях
Финансовые аналитики используют коэффициенты вариации для оценки инвестиционных рисков для принятия более эффективных решений. При наличии нескольких вариантов инвестирования коэффициент вариации помогает сравнить оба варианта с точки зрения рисков и доходности и выбрать вариант с наибольшей рентабельностью инвестиций.
Исследуйте: Шаблоны финансовых форм
Предположим, что инвестиция А имеет стандартное отклонение 5 % и 10 % рентабельности инвестиций, а инвестиция Б имеет предполагаемую рентабельность инвестиций 15 % и стандартное отклонение 10 %.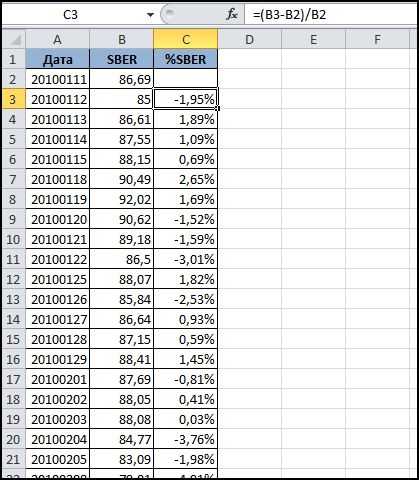 Применяя формулу COV, вы обнаружите, что инвестиции А имеют более низкие инвестиционные риски.
Применяя формулу COV, вы обнаружите, что инвестиции А имеют более низкие инвестиционные риски.
Коэффициент вариации также можно использовать для измерения жизнеспособности новых рынков до того, как организация запустит новый продукт, услугу или торговую точку. Вы можете сравнить прогнозируемые затраты на проникновение на рынок для двух территорий и выбрать вариант с меньшими вариациями.
Приложение 3Исследователи используют коэффициенты вариации для сравнения результатов систематических исследований различных групп населения. Например, вы можете использовать COV для измерения изменчивости расходов среди домохозяйств с высоким доходом и домохозяйств с низким доходом.
Решаемые примеры с участием COV Formula Пример 1Средний доход представлен со следующим инвестиционным вариантом:
Вариант A: Cryptocurrence
Возвращение на инвестиции: 25%
. : 15%
: 15%
Вариант B: Казначейские векселя
Возврат инвестиций: 5%
Волатильность: 0,75%
COV = (Волатильность ÷ ROI) × 5 100
COV 900 %) × 100 = 60%
COV (Вариант B) = (0,75% ÷ 5%) × 100 = 15%
Исходя из этого, вариант B представляет для инвесторов меньшую волатильность.
Пример 2После проведения систематического исследования лиц с высоким и низким доходом в сообществе исследователь получил следующие результаты: Среднее значение: 600 000 долларов
Лица с низким доходом
Среднее значение: 35 000 долл. США
Стандартное отклонение: 5 000 долл. США
Коэффициент вариации (для лиц с высоким доходом) = (100 000 долл. США ÷ 600 000 долл. США) × 100 = 16,6%
Коэффициент вариации (для лиц с низким доходом) 100 = 14,3%
Практическое ограничение формулы коэффициента вариации Коэффициент вариации измеряет изменчивость с использованием шкал отношений.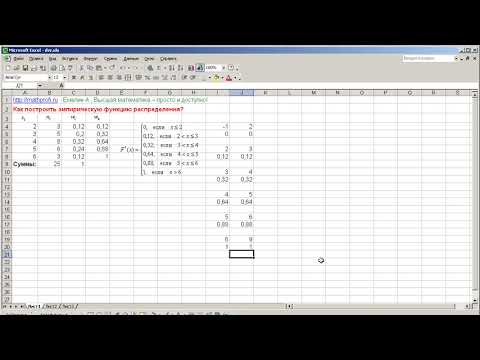 Это означает, что его нельзя использовать для построения доверительных интервалов для среднего значения, в отличие от стандартного отклонения.
Это означает, что его нельзя использовать для построения доверительных интервалов для среднего значения, в отличие от стандартного отклонения.
При более глубоком изучении коэффициента вариации вы столкнетесь с несколькими связанными понятиями, включая среднее значение, стандартное отклонение и дисперсию. Понимание этих связанных концепций поможет вам точно применять коэффициенты вариации к вашим наборам данных. Давайте обсудим некоторые из них в этом разделе.
ДисперсияДисперсия или изменчивость учитывают распределение числовых значений в рамках статистической функции. Исследователи полагаются на изменчивость, чтобы знать, как далеко точки данных находятся друг от друга и от центра распределения.
Дисперсия позволяет исследователям узнать, насколько однородны или неоднородны наборы данных, при интерпретации изменчивости отдельных значений. Вы можете измерить распределение в исследовательских данных, используя диапазон, дисперсию и стандартное отклонение.
Вы можете измерить распределение в исследовательских данных, используя диапазон, дисперсию и стандартное отклонение.
Статистики делят дисперсию на две части:
- Абсолютная мера дисперсии
- Относительная мера рассеивания
1. Абсолютная мера рассеивания
Абсолютные меры дисперсии используются для определения количества распределения в рамках одного набора наблюдений. По замыслу результаты абсолютных показателей дисперсии всегда находятся в тех же единицах измерения, что и исходные наборы данных. Например, если точки данных указаны в метрах, абсолютные меры также будут метрами.
В зависимости от цели вашего исследования и наборов числовых данных вы можете использовать один или несколько следующих типов абсолютных мер дисперсии:
- Диапазон
- Дисперсия и стандартное отклонение
- Квартили и квартильное отклонение
- Среднее и среднее отклонение
Плюсы использования абсолютных показателей дисперсии
- Их относительно просто понять и рассчитать.

- Абсолютные меры дисперсии ограничивают любые искажения, вызванные экстремальными оценками в наборах данных, особенно когда вы зависите от среднего отклонения.
Минусы использования абсолютных мер дисперсии
- Они могут привести к неуместным или непрактичным результатам.
- Процессы вычисления абсолютных показателей дисперсии могут быть сложными, особенно если вы имеете дело с большим набором данных.
2. Относительная мера дисперсии
С другой стороны, исследователи используют относительные меры дисперсии для сравнения распределения двух или более наборов данных. В отличие от абсолютных мер дисперсии, относительные меры не учитывают единицу исходного наблюдения. Применяя относительные меры к наборам данных, вы получите результат, похожий на отношение, который также считается коэффициентом.
Общие методы относительной дисперсии включают:
- Коэффициент диапазона
- Коэффициент вариации
- Коэффициент стандартного отклонения
- Коэффициент квартильного отклонения
- Коэффициент среднего отклонения
Плюсы использования методов относительной дисперсии
- Методы относительной дисперсии позволяют сравнивать два или более статистических ряда.

- Они помогают исследователям контролировать изменчивость явления.
Минусы использования методов относительной дисперсии
- Они могут привести к неправильным интерпретациям и обобщениям в наборах данных.
- Они могут давать неправильные результаты, так как существуют разные методы расчета дисперсии.
Среднее значение относится к среднему значению набора данных. Вы также можете думать об этом как о самой распространенной переменной в наборе наблюдений для исследования. Его можно использовать для линейных и простых наборов данных, а также для более сложных наблюдений.
Статистики называют среднее значением центральной тенденции, поскольку оно учитывает все значения в наборе данных, особенно экстремальные переменные. Это позволяет легко определить идеальную среднюю точку ваших исследовательских данных.
Хотя среднее арифметическое является наиболее распространенным типом этой меры центральной тенденции, существуют также средневзвешенное значение, среднее геометрическое (GM) и среднее гармоническое (HM).
Как рассчитать среднее значениеЧтение: Зависимые и независимые переменные: 11 ключевых отличий
Среднее = сумма всех переменных ÷ количество переменных в размере выборки
Давайте применим эту формулу к работе.
Предположим, что организация имеет 1500 переменных в сумме 15 переменных в размере исследовательской выборки. В этом случае среднее значение набора данных равно 100.
Плюсы использования среднего значения в статистике- Он обеспечивает объективное представление различных переменных в наборе данных.
- Ограничивает влияние экстремальных значений в больших выборках исследований.
- Он чувствителен к экстремальным значениям в небольшом наборе данных.
- Среднее — не самая подходящая мера центральной тенденции асимметричного распределения.

Стандартное отклонение несколько похоже на дисперсию и изменчивость. Однако в этом случае стандартное отклонение измеряет распределение значений в наборе данных относительно его среднего значения. Как только вы узнаете дисперсию или дисперсию для ваших данных, вы можете взять квадратный корень из этого значения, чтобы определить стандартное отклонение.
Высокое стандартное отклонение показывает, что отдельные переменные, как правило, далеки от среднего в типичных распределениях данных. Напротив, низкое стандартное отклонение указывает на то, что значения данных тесно сгруппированы вокруг среднего значения.
Как рассчитать стандартное отклонение в исследованияхШаг 1: Рассчитайте среднее арифметическое вашего набора данных.
Шаг 2: Вычтите среднее из каждой оценки, чтобы получить отклонения от среднего.
Шаг 3: Возведите в квадрат каждое отклонение от среднего значения. Это приведет к положительным числам.
Это приведет к положительным числам.
Шаг 4: Найдите сумму квадратов отклонений.
Шаг 5: Найдите дисперсию наборов данных.
Шаг 6: Возьмите квадратный корень из дисперсии, чтобы получить стандартное отклонение.
Основная формула стандартного отклонения выглядит следующим образом:
Где;
s = стандартное отклонение выборки
∑ = сумма…
X = каждое значение
x̅ = среднее значение выборки
n = количество значений в выборке
Плюсы использования стандартного отклонения в опросных исследованиях- Стандартное отклонение дает вам лучшее представление о изменчивости ваших данных, чем более простые меры вариации.
- При возведении в квадрат различий от среднего стандартное отклонение более точно отражает неравномерную дисперсию.
- Он подвержен экстремальным значениям в наборах данных.
- Стандартное отклонение не дает полного диапазона данных.

- Определение
Стандартное отклонение — это статистическая величина, учитывающая разброс набора данных относительно его среднего значения. При этом коэффициент вариации представляет собой отношение стандартного отклонения к его среднему значению.
- Назначение
Как стандартное отклонение, так и коэффициент вариации рассчитывают вариации в исходном наборе данных. Однако коэффициент вариации идет дальше, чтобы определить отношение изменчивости среднего значения набора данных.
- Когда использовать
Если вы хотите сравнить изменчивость измерений, выполненных в разных единицах, то коэффициент изменчивости является в этом случае ценным показателем. Однако расчет стандартного отклонения может быть полезен, если вы хотите определить погрешность или волатильность в ваших наборах данных.
- Преимущества коэффициента вариации
Одним из существенных преимуществ коэффициента вариации является то, что он не имеет единиц измерения, и его можно применять к любому данному количественному наблюдению. Это позволяет сравнивать степень вариации между двумя разными наборами данных.
- Преимущества стандартного отклонения
Стандартное отклонение дает четкое представление о распределении данных в наблюдении. Он также служит защитой от эффектов экстремальных значений или выбросов в количественных наблюдениях.
Коэффициент вариации по сравнению с дисперсией- Определение
Дисперсия — это мера изменчивости, которая показывает степень разброса в вашем наборе данных с использованием более крупных единиц измерения, таких как метры в квадрате. С другой стороны, коэффициент вариации измеряет относительное распределение точек данных вокруг среднего значения.
- Когда использовать
Используйте дисперсию или тесты дисперсии для оценки различий между популяциями или группами в вашем исследовании. Между тем, коэффициент вариации позволяет сравнивать степень изменчивости между разными наборами данных.
- Преимущества варианта
Вариантность помогает получить полезную информацию о наборе данных для принятия более эффективных решений. Дисперсия обрабатывает все числа в наборе одинаково, независимо от того, являются ли они положительными или отрицательными, что позволяет учитывать минимальную изменчивость в наборах данных.
- Преимущества коэффициента вариации над дисперсией
Коэффициент вариации помогает измерить степень согласованности и единообразия в распределении ваших наборов данных. В отличие от дисперсии, она не зависит от единицы измерения исходных данных, что позволяет сравнивать два разных распределения.
1. Есть ли единицы измерения COV?
Нет. Коэффициент вариации является безразмерной мерой относительной дисперсии. Отсутствие единиц позволяет использовать COV для сравнения изменчивости взаимоисключающих наборов данных.
2. Что такое плохой коэффициент вариации?
Если коэффициент вариации больше 1, это указывает на относительно высокую изменчивость наборов данных. С другой стороны, CV ниже 1 считается низкой дисперсией.
3. Что такое приемлемый коэффициент вариации?
Коэффициент вариации зависит от состава точек данных в вашем наблюдении. В целом допустим коэффициент вариации от 20 до 30, в то время как COV выше 30 неприемлем.
4. Может ли коэффициент вариации быть отрицательным?
Да. Если среднее значение ваших данных отрицательное, то и коэффициент вариации будет отрицательным. Однако это обычно означает, что коэффициент вариации вводит в заблуждение.
Однако это обычно означает, что коэффициент вариации вводит в заблуждение.
5. Какая формула используется для расчета коэффициента вариации?
Коэффициент вариации = (Стандартное отклонение ÷ Среднее) × 100% и стандартное отклонение. Хотя вам не всегда нужно применять коэффициент вариации к своим наборам данных, полезно знать, как он работает и как он влияет на исследования.
Создание опросов бесплатно
Функция RSQ
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Дополнительно… Меньше
В этой статье описаны синтаксис формулы и использование RSQ . функция в Microsoft Excel.
Описание
Возвращает квадрат коэффициента корреляции момента произведения Пирсона по точкам данных в known_y и known_x. Для получения дополнительной информации см. функцию PEARSON. Значение r-квадрата можно интерпретировать как долю дисперсии y, относящуюся к дисперсии x.
Для получения дополнительной информации см. функцию PEARSON. Значение r-квадрата можно интерпретировать как долю дисперсии y, относящуюся к дисперсии x.
Синтаксис
RSQ(известные_y,известные_x)
Синтаксис функции RSQ имеет следующие аргументы:
Замечания
Аргументы могут быть числами или именами, массивами или ссылками, содержащими числа.
Подсчитываются логические значения и текстовые представления чисел, которые вы вводите непосредственно в список аргументов.
Если аргумент массива или ссылки содержит текст, логические значения или пустые ячейки, эти значения игнорируются; однако включаются ячейки с нулевым значением.

Аргументы, которые являются значениями ошибок или текстом, который не может быть преобразован в числа, вызывают ошибки.
Если известные_y и известные_x пусты или имеют разное количество точек данных, RSQ возвращает значение ошибки #Н/Д.
Если известные_у и известные_х содержат только 1 точку данных, RSQ возвращает #DIV/0! значение ошибки.
Уравнение для коэффициента корреляции момента продукта Пирсона, r, имеет вид:
, где x и y — выборочные средние значения AVERAGE (известные_x) и AVERAGE (известные_y).

RSQ возвращает r2, который является квадратом этого коэффициента корреляции.
Пример
Скопируйте данные примера из следующей таблицы и вставьте их в ячейку A1 нового рабочего листа Excel. Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите клавишу ВВОД. При необходимости вы можете настроить ширину столбцов, чтобы увидеть все данные.
Данные | ||
Известен | Известно x | |
2 | 6 | |
3 | 5 | |
9 | 11 | |
1 | 7 | |
8 | 5 | |
7 | 4 | |
5 | 4 | |
Формула | Описание | Р результат |
=RSQ(A3:A9, B3:B9) | Квадрат коэффициента корреляции момента произведения Пирсона по точкам данных в A3:A9 и B3:B9. | 0,05795 |
Коэффициент вариации в таблицах Excel/Google
В этой статье речь пойдет о том, как рассчитать коэффициент вариации по формуле в электронной таблице Microsoft Excel или Google Sheets.
Что такое коэффициент вариации?
Коэффициент вариации представляет собой отношение стандартного отклонения исходных данных к среднему значению исходных данных. Коэффициент вариации не имеет шкалы, поэтому можно провести объективное сравнение. Фактически, коэффициент вариации можно рассматривать как абсолютную величину, отражающую степень разброса данных, точно так же, как экстремальное отклонение, стандартное отклонение и дисперсию. На размер его данных влияет не только степень дисперсии значений переменных, но и размер среднего значения переменных.
Расчет коэффициента вариации
Коэффициент вариации рассчитывается как:
C.V = (стандартное отклонение / среднее значение) × 100%
Если коэффициент вариации мал, степень вариации (отклонения) мала и риск небольшой; и наоборот, если коэффициент вариации велик, степень вариации (отклонения) велика и риск велик.
Примечание: На величину коэффициента вариации влияют статистика среднего значения и стандартного отклонения, поэтому при использовании коэффициента вариации для выражения степени вариации информации лучше указывать как среднее значение, так и стандартное отклонение.
Общая формула
Вы можете использовать следующую общую формулу в Excel или Google Sheets для расчета коэффициента вариации следующим образом.
=STEDDV.P(A1:A5)/СРЗНАЧ(A1:A5)
где A1:A5 — выборочные данные для расчета, и данные должны находиться в одной строке.
Объяснение формулы
Давайте объясним, как работает приведенная выше общая формула. Для того, чтобы рассчитать коэффициент вариации в таблицах Excel или google, вам нужно использовать Функция СТАНДОТКЛОН. П в формуле в сочетании с функцией СРЗНАЧ . В примере из этой статьи вам нужно ввести следующую формулу в ячейку h4.
П в формуле в сочетании с функцией СРЗНАЧ . В примере из этой статьи вам нужно ввести следующую формулу в ячейку h4.
=СТАНДОТКЛОН.П(A3:E3)/СРЗНАЧ(A3:E3)
Вам необходимо рассчитать стандартное отклонение, используя формулу СТАНДОТКЛОН.П , введя следующую формулу в ячейку G3.
=STDEV.P(A3:E3)
Затем перетащите обработчик заполнения в ячейку G4 и примените приведенную выше формулу. Вы увидите, что разница между значениями стандартного отклонения в G3 и G4 очень мала. Итак, чтобы различать степень их вариации, нужно рассчитать коэффициент вариации, что можно сделать, введя в ячейку h4 следующую формулу.
=G3/СРЗНАЧ(A3:E3)
Эта формула сначала вычисляет среднее значение диапазона A3:E3 , а затем делит среднее значение на стандартное отклонение значение в G3 , так что коэффициент вариации можно вычислить. Затем вам нужно будет перетащить обработчик заполнения из ячейки h4 в ячейку h5, чтобы применить приведенную выше формулу.
Из значений в h4,h5 видно, что разница по-прежнему значительна.
Вопросы и ответы
1. Что такое CV Instatistics Excel?
Коэффициент вариации, также известный как «коэффициент стандартного отклонения », является еще одним статистическим показателем, который измеряет степень вариации наблюдений в наборе данных. При сравнении степени вариации двух или более данных, если единицы измерения совпадают со средним значением, стандартное отклонение можно использовать непосредственно для сравнения. Если единицы измерения и/или среднее значение различаются, степень вариации нельзя сравнивать с использованием стандартного отклонения, а скорее отношением стандартного отклонения к среднему (относительному значению).
Отношение стандартного отклонения к среднему значению называется коэффициентом вариации или C.V. Коэффициент вариации устраняет влияние различных единиц и/или средств на сравнение степени вариации двух или более данных.
2. Как рассчитать коэффициент вариации?
Формула для расчета коэффициента вариации: Коэффициент вариации = (стандартное отклонение/среднее) × 100%.
3. Зачем нужно рассчитывать коэффициент вариации?
Когда вам нужно сравнить два набора данных, если масштабы измерения двух наборов данных слишком разные или существуют различия в масштабах данных, их нецелесообразно сравнивать напрямую со стандартным отклонением, тогда вам придется исключить влияние шкалы измерения, и это может сделать коэффициент вариации, он представляет собой отношение стандартного отклонения исходных данных к среднему значению исходных данных.
4. В чем разница между коэффициентом вариации и стандартным отклонением?
Как стандартное отклонение, так и коэффициент вариации являются общими статистическими показателями, используемыми для описания разброса данных.
Стандартное отклонение: Это абсолютный показатель дисперсии каждого наблюдения, основанный на среднем арифметическом. Стандартное отклонение нельзя использовать для сравнения дисперсии двух наборов данных, когда общее среднее значение отличается или когда разные единицы измерения.
Стандартное отклонение нельзя использовать для сравнения дисперсии двух наборов данных, когда общее среднее значение отличается или когда разные единицы измерения.
Коэффициент вариации: Отношение стандартного отклонения к среднему значению называется коэффициентом вариации и обозначается как C.V. Коэффициент вариации устраняет влияние различных единиц и/или средств на сравнение степени вариации двух или более данных.
5. Что такое коэффициент вариации и есть ли у вас пример?
Какая из двух пород взрослых свиноматок имеет большую степень вариации веса, когда средний вес взрослых свиноматок в племенной ферме составляет 200 кг при стандартном отклонении 10 кг, а средний вес взрослых свиноматок в категории B составляет 206 кг со стандартным отклонением 8 кг.
Хотя наблюдаемые значения в этом случае имеют одинаковый вес на единицу, их средние значения не одинаковы, и коэффициент вариации можно использовать только для сравнения степени их вариации.

 А в ячейке теперь отобразится результат из взятых данных выше.
А в ячейке теперь отобразится результат из взятых данных выше. На их долю приходится до 10 % от общих объемов ресурсов.
На их долю приходится до 10 % от общих объемов ресурсов. Всегда должны быть в наличии (выделены желтым цветом на рисунке). Спрос на такие товары стабильный, он не имеет сезонных колебаний и относительно постоянный.
Всегда должны быть в наличии (выделены желтым цветом на рисунке). Спрос на такие товары стабильный, он не имеет сезонных колебаний и относительно постоянный.






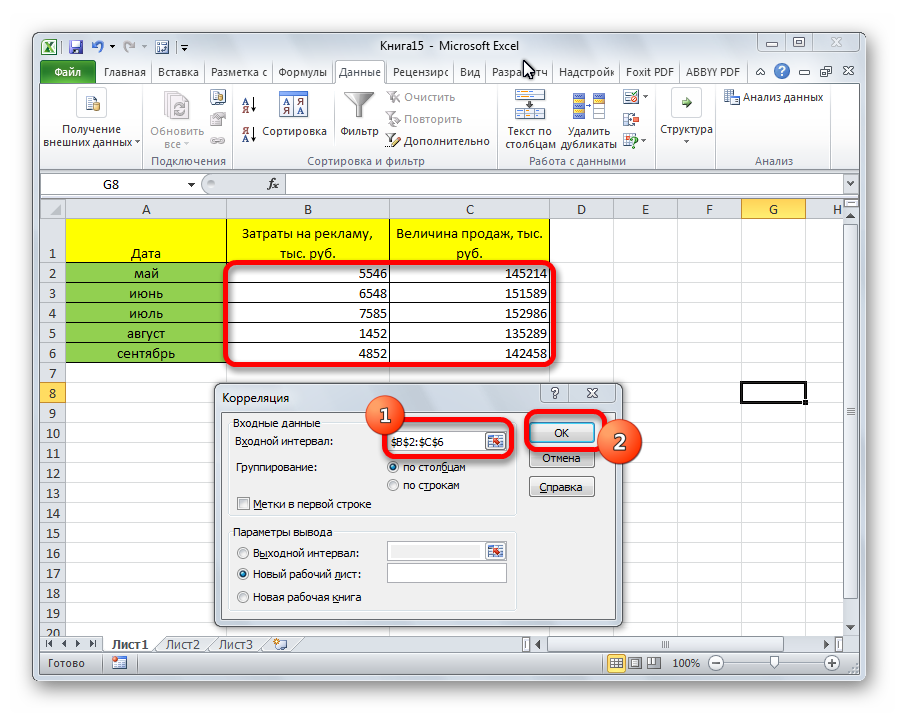 V = (стандартное отклонение / среднее значение) × 100%
V = (стандартное отклонение / среднее значение) × 100%