Расчет показателей вариации
Тарифный разряд, x | Число рабочих, f | |d|f | d2f | |
2 | 4 | -1,8 | 7,2 | 12,96 |
3 | 5 | -0,8 | 4,0 | 3,20 |
9 | +0,2 | 1,8 | 0,36 | |
5 | 4 | +1,2 | 4,8 | 5,76 |
6 | 2 | +2,2 | 4,4 | 9,68 |
Итого | 24 | 22,2 | 31,96 |
Следовательно,
индивидуальные значения отличаются в
среднем от средней арифметической на
1,15 разряда, или на 30,3%.
Среднее квадратическое отклонение превышает среднее линейное отклонение в соответствии со свойствами мажорантности средних.
Значение коэффициента вариации (30,3%) свидетельствует о том, что совокупность достаточно однородна.
Как видно на рис. 3.1, распределение рабочих по тарифному разряду несимметрично, поэтому определяется показатель асимметрии:
Следовательно, асимметрия левосторонняя, незначительная.
2. Имеются следующие данные о возрастном составе рабочих цеха (лет): 18; 38; 28; 29; 26; 38; 34; 22; 28; 30; 22; 23; 35; 33; 27; 24; 30; 32; 28; 25; 29; 26; 31; 24; 29; 27; 32; 25; 29; 29.
Для анализа распределения рабочих цеха по возрасту требуется:
1) построить интервальный ряд распределения;
2) дать графическое изображение ряда;
3) исчислить
показатели центра распределения,
показатели вариации и формы распределения.
Сформулировать вывод.
Решение
1. Величина интервала группировки определяется по формуле
где т принимаем равным 7.
Интервальный ряд распределения
Группы рабочих по возрасту (лет), х | Число рабочих, f | Накопленная частота, S |
18-21 | 1 | 1 |
21 –24 | 3 | 4 |
24-27 | 6 | 10 |
27-30 | 10 | 20 |
30-33 | 5 | 25 |
33-36 | 3 | 28 |
36-39 | 2 | 30 |
Итого 30 | 30 | — |
2.
Графически
интервальный вариационный ряд может
быть представлен в виде гистограммы,
полигона, кумуляты.
Гистограмма строится в прямоугольной системе координат. По оси абсцисс откладывают интервалы значений вариационного признака, причем число интервалов целесообразно увеличить на два (по одному в начале и в конце имеющегося ряда) для удобства преобразования гистограммы в полигон частот. На отрезках (интервалах) строятся прямоугольники, высота которых соответствует частоте.
Для преобразования гистограммы в полигон частот середины верхних сторон прямоугольников соединяют отрезками прямой, и две крайние точки прямоугольников замыкаются по оси абсцисс на середине интервалов, в которых частоты равны нулю. На рис. 2 представлено графическое изображение построенного интервального вариационного ряда в виде гистограммы и полигона частот.
Как видно из
графика, треугольники, относящиеся к
площади гистограммы и к площади полигона,
попарно равны между собой, и, следовательно,
площадь гистограммы и площадь полигона
данного вариационного ряда также
совпадают.
На основе построенной гистограммы графически можно определить значение моды. Для этого правую вершину модального прямоугольника соединяют прямой с правым верхним углом предыдущего прямоугольника, а левую вершину модального прямоугольника соединяют с левым верхним углом последующего прямоугольника. Абсцисса точки пересечения этих прямых и будет модой распределения. Мо = 28,3 года. На рис. 2 эти прямые линии, соединяющие вершины прямоугольников, и перпендикуляр из точки их пересечения показаны пунктирной линией.
На рис. 3 представлена кумулятивная кривая (кумулята).
Кумулята
может быть использована для графического
определения медианы. Для этого последнюю
ординату кумуляты делят пополам. Через
полученную точку проводят прямую,
параллельную оси х, до пересечения ее
с кумулятой. Из точки пересечения
опускается перпендикуляр до оси абсцисс.
Абсцисса точки пересечения является
медианой. Линии, определяющие медиану,
на рис. 3 показаны пунктирными линиями.
Рис. 2. Гистограмма и полигон распределения рабочих цеха по возрасту
Рис. 3. Кумулята распределения рабочих цеха по возрасту
3. Расчет показателей центра распределения:
где х’ — среднее значение признака в интервале (центр интервала).
Для интервального вариационного ряда порядок расчета структурных средних следующий: сначала находят интервал, содержащий моду или медиану, а затем рассчитывают соответствующие значения названных показателей.
Модальным в данном распределении является интервал 27 — 30 лет, так как наибольшее число рабочих (f= 10) находится в этом интервале. Значение моды определяется по формуле
Значение моды, полученное по формуле, соответствует значению, полученному на графике.
Место медианы – года
Медианным
является также интервал 27 — 30 лет, так
как в этом интервале находятся номера
15 и 16 ряда.
Для расчета показателей вариации составляется вспомогательная таблица (табл. 2.).
Следовательно, вариация возраста у рабочих данного цеха не является значительной, что подтверждает достаточную однородность совокупности.
Таблица для расчета показателей вариации
Группы рабочих по возрасту, лет | Центр интервала, лет (x’) | f | x’f | |d|f | d2 | d2f | |
18-21 | 19,5 | 1 | 19,5 | -9,2 | 9,2 | 84,64 | 84,64 |
21-24 | 22,5 | 3 | 67,5 | -6,2 | 18,6 | 38,44 | 115,32 |
24-27 | 25,5 | 6 | 153,0 | -3,2 | 19,2 | 10,24 | 61,44 |
27-30 | 28,5 | 10 | 285,0 | -0,2 | 20,0 | 0,04 | 0,40 |
30-33 | 31,5 | 5 | 157,5 | 2,8 | 14,0 | 7,84 | 39,20 |
33-36 | 34,5 | 3 | 103,5 | 5,8 | 17,4 | 33,64 | 100,92 |
36-39 | 37,5 | 2 | 75,0 | 8,8 | 17,6 | 77,44 | 154,88 |
Итого | — | 30 | 861,0 | — | 116,0 | — | 556,80 |
Как видно на рис.
2, распределение рабочих по возрасту
несимметрично, поэтому определяется
показатель асимметрии:
Следовательно, асимметрия правосторонняя, незначительная. При правосторонней асимметрии между показателями центра распределения существует соотношение
Mo < Me < .
Для данного распределения это соотношение выполняется, т. е. 28,33 < 28,65 < 28,70. При левосторонней асимметрии (AS со знаком минус) соотношение между показателями центра распределения будет иметь вид:
Mo > Me > .
Для имеющегося распределения, учитывая незначительную асимметрию, целесообразно определить показатель эксцесса (островершинности):
где 4 — центральный момент четвертого порядка;
Отрицательное значение эксцесса свидетельствует о плосковершинности распределения.
3.
Имеются следующие
данные о времени простоя автомобиля
под разгрузкой:
№ пункта разгрузки | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Число грузчиков | 3 | 4 | 4 | 3 | 3 | 4 | 4 | 4 | 3 | 4 |
Время про- стоя, мин | 12 | 10 | 8 | 15 | 19 | 12 | 8 | 10 | 18 | 8 |
Проверить закон
сложения дисперсий.
Показатели коэффициент вариации — Энциклопедия по экономике
Следующий показатель — коэффициент вариации, который характеризует величину риска на единицу ожидаемого результата и рассчитывается по формуле [c.289]Данный коэффициент показывает степень отклонения полученных значений. Он является относительной величиной, поэтому на его размер не оказывают влияния абсолютные значения изучаемого показателя. Коэффициент вариации может изменяться от 0 до 100%. Чем больше коэффициент, тем сильнее колеблемость и, следовательно, выше риск. Установлена следующая качественная оценка различных значений коэффициентов вариации [c.274]
Показатели и методы изучения колеблемости цен. Направления изучения вариации цен и их особенности. Проблемы расчета коэффициента вариации региональных цен. Показатели и методы исследования цикличности и сезонности цен.
Вариация цен при наличии и изменении тенденции.
[c.145]
Для общей характеристики структуры процесса, явления используют показатели размаха отклонений (максимального уровня от минимального), среднеквадратичного отклонения и коэффициента вариации. Простейшим показателем вариации служит размах колебаний А — разность максимальных и минимальных значений рассматриваемых показателей [c.20]
Проведя детализацию показателей суточной производительности во времени, можно оценить стабильность работы установки, рассчитав показатель размаха А, среднеквадратичное отклонение а и коэффициент вариации v [c.46]
Предварительное исследование полученной выборки (дисперсионный анализ, определение закона распределения выборки и т. д.) позволяет в определенных пределах оценить значимость факторов по таким показателям, как размах варьирования, дисперсия и коэффициент вариации. Эти показатели характеризуют степень рассеивания наблюдаемых величин и свойства эмпирического наблюдения, что в определенной мере дополняет полученные ранее сведения о-характере влияния отобранных факторов.
[c.16]
Высокая колеблемость наблюдается и по некоторым факторам. Так, коэффициент вариации V в % составляет для показателей [c.26]
Прямые показатели — коэффициент ритмичности, коэффициент вариации, удельный вес производства продукции за /-и период (декаду, месяц, квартал) в годовом объеме производства. [c.112]
Однородность информации оценивается в зависимости от относительного ее распределения около среднего уровня. Критериями служат среднеквадратическое отклонение и коэффициент вариации, определяемые по каждому факторному и результативному показателю. [c.75]
Таким образом, в приложении к финансовым операциям речь идет об оценке вариабельности ожидаемого дохода (доходности), а в качестве критериев оценки можно использовать такие статистические коэффициенты, как размах вариации, дисперсия, среднее квадратическое отклонение, называемое иногда стандартным, и коэффициент вариации. Дадим краткую характеристику этим показателям, имея ввиду, что в случае необходимости читатель может найти более подробную
[c.
83]
Все вышеприведенные показатели обладают одним общим недостатком — это абсолютные показатели, значение которых существенно зависит от абсолютных значений исходного признака ряда. Поэтому большее применение имеет коэффициент вариации, рассчитываемый по формуле [c.84]
Для оценки выполнения плана по ритмичности используются прямые и косвенные показатели. Прямые показатели — коэффициент ритмичности, коэффициент вариации, коэффициент аритмичности, удельный вес производства продукции за каждую декаду (сутки) к месячному выпуску, удельный вес произведенной продукции за каждый месяц к квартальному выпуску, удельный вес выпущенной продукции за каждый квартал к годовому объему производства, удельный вес продукции, выпущенной в первую декаду отчетного месяца, к третьей декаде предыдущего месяца. [c.458]
Некоторое представление о колеблемости уровней процентных ставок в рассматриваемом периоде дает показатель размаха вариации. Однако эта абсолютная величина отражает колеблемость процентных ставок в пределах экстремальных значений признака.
Более точными измерителями колеблемости являются дисперсия, среднее квадратическое отклонение и коэффициент вариации.
[c.606]
Как видно из таблицы результатов расчета показателей вариации, колеблемость процентных ставок в 1996 г. сравнительно невысокая. Коэффициенты вариации отдельных видов процентных ставок изменяются в пределах от 13,32 до 28,51%. [c.606]
С целью окончательного выбора формы тренда сопоставляют показатели вариации (дисперсию, среднее квадратическое отклонение и коэффициент вариации) эмпирических данных от- [c.613]
Значения показателей вариации, которые рассчитывают для уточнения формы тренда процентных ставок, могут оказаться достаточно высокими (например, коэффициент вариации составляет 35% и более), что свидетельствует о широкой амплитуде колебаний уровней фактических данных относительно выравненных. Это позволяет предположить, что динамика показателя складывалась под воздействием различных факторов, в том числе циклических, сезонных и случайных.
[c.614]
При изучении изменчивости валютных курсов используют известный статистический инструментарий, исчисляя размах колебаний валютных курсов (R), дисперсию (52), стандартное (среднее) квадратическое отклонение ( ), коэффициент вариации (V). Можно исчислить показатели вариации по различным валютам во времени, а также по какой-либо одной валюте исходя из котировок на различных валютных площадках и секторах рынка. Первый показатель позволит выделить наиболее надежную валюту, второй — наиболее устойчивый валютный рынок. [c.657]
Теоретическая статистика разрабатывает и изучает содержание, форму, методы расчета этих показателей в общем виде что такое средняя арифметическая величина, коэффициент вариации, уравнение тренда ряда динамики. Если же любой из этих показателей рассчитан для определенного объекта, признака, периода времени, то он становится уже конкретным показателем, например в главе 9 Статистическое изучение динамики показатели сезонных колебаний импорта КНР за 1992-1995 гг.
— это уже конкретные статистические показатели экономики Китая.
[c.46]
Рассмотренные направления проверки статистических гипотез охватывают лишь важнейшие из них. Процедура испытания статистических гипотез применяется для определения того, случайно или нет полученное значение коэффициента корреляции, коэффициента вариации и т. д., случайны или нет различия в значениях показателей (медиан, коэффициентов корреляции, регрессии и т.д.) в разных [c.217]
Оба квадрата корреляционных отношений соответствуют по содержанию ранее рассмотренному коэффициенту детерминации (8.1) и (8.2) и интерпретируются как показатели доли вариации результативного признака, объясняемой за счет вариации группировочно-го, факторного признака (и, конечно, связанных с ним прочих факторов). В данном примере связь является тесной. Различие в том, что в эмпирическом корреляционном отношении связь признаков не абстрагирована от случайных влияний прочих факторов на вариацию у, не связанных с вариацией х.
[c.255]
На основе качественного содержания понятия колеблемости строится и система ее показателей. Показателями силы колебаний уровней являются амплитуда отклонений уровней отдельных периодов или моментов от тренда (по модулю), среднее абсолютное отклонение уровней от тренда (по модулю), среднее квадратическое откло нение уровней от тренда. Относительные меры колеблемости относительное линейное отклонение от тренда и коэффициент колеблемости — аналог коэффициента вариации. [c.341]
Для оценки ритмичности поставок используются показатели среднеквадратичное отклонение фактического объема поставки по дням (декадам, месяцам) от среднего объема поставки коэффициент неравномерности поставок и коэффициент вариации [c.239]
Коэффициент вариации — величина относительная, поэтому на его размер не оказывают влияния абсолютные значения изучаемого показателя. С помощью коэффициента вариации можно сравнивать даже колеблемость признаков, вы- [c.41]
Коэффициент вариации показывает, что если отклонение расчетных показателей от фактических незначительно, то модель пригодна для планирования (прогнозирования) прибыли.
[c.323]
Для оценки ритмичности поставок используются следующие показатели коэффициент ритмичности число аритмичности среднее квадратичное отклонение коэффициент неравномерности поставок коэффициент вариации. [c.357]
Т Определение. Коэффициент вариации — это особый показатель вариации, получаемый путем соотношения среднеквадратического отклонения и арифметической средней и выражаемый в процентах. А [c.46]
Следует отметить, что в отличие от других значений, представленных в данном разделе, коэффициент вариации не является овеществленной мерой разброса. Например, при рассмотрении заработной платы большинство показателей выражены в используемой денежной единице, скажем, в фунтах стерлингов. В противоположность этому коэффициент вариации не зависит от используемой единицы измерения. [c.46]
Так как коэффициент вариации для предложения В превышает аналогичный показатель для предложения А, мы можем сказать, что предложение В имеет более высокую степень риска.
Можно поставить вопрос о целесообразности использования коэффициента вариации, ведь в нашем примере большая величина стандартного отклонения для предложения В уже свидетельствует о том, что оно более рискованное. Но сравнивать стандартное отклонение мы можем потому, что математические ожидания вероятностных распределений в нашем примере для обоих предложений были одинаковыми. А если бы они были разными В таком случае нам и нужен критерий относительной дисперсии, которым является коэффициент вариации. Математическое ожидание, стандартное отклонение и коэффициент вариации будут часто упоминаться в дальнейшем в этой главе.
[c.390]
В рассматриваемом примере коэффициент вариации составляет для проекта А = 7.03/30 = 0,24, для проекта В— 14,1/30 = 0,47. Чем выше коэффициент вариации, тем больше размер риска на единицу результата. Следовательно, проект б, имеющий более высокий коэффициент вариации, является более рисковым. В нашем примере решения о степени рисковости проектов можно было принять, не прибегая к расчету коэффициента вариации, а используя только показатели дисперсии или стандартного отклонения, так как математическое ожидание вероятностного распределения у обоих проектов одинаковое.
Если же показатели математического ожидания вероятностного распределения различаются, то вывод об уровне риска проектов сделать на основе только показателей дисперсии и стандартного отклонения не представляется возможным. Проиллюстрируем это на примере двух проектов Си D (табл. 24.2). Рассматриваются также три сценария событий оптимистический (вероятность совершения которого составляет 75%), средний (50%) и пессимистический (25%).
[c.353]
В практике использования этого алгоритма размер возможных финансовых потерь выражается обычно абсолютной суммой, а вероятность возникновения инвестиционного риска — одним из коэффициентов измерения этой вероятности (коэффициентом вариации, бета-коэффициентом и др.) Соответственно уровень инвестиционного риска при его расчете по данному алгоритму будет выражен абсолютным показателем, что существенно снижает базу его сравнения при рассмотрении альтернативных вариантов. [c.150]
Общая структура процесса, явления характеризуется такими показателями, как максимальный и минимальный уровни, сред-неквадратическое отклонение и коэффициент вариации.
Простейшим показателем вариации служит разность максимальных и минимальных значений рассматриваемых показателей (А). Однако этот показатель зависит от крайних значений и плохо характеризует изменения всех показателей в целом. Более полно степень колеблемости отражают среднеквадратическое отклонение а) и коэффициент вариации (V). Последний определяется отношением среднеквадратического отклонения к среднеарифметической величине и отражает стабильность, устойчивость процесса.
[c.141]
Ввиду ограниченности количества данных при работе с двумя сопоставимыми отклоняющими компоновками необходимо установить точность и надежность средних значений показателей работы долот в обоих вариантах, а также выяснить, случайно или не случайно различие между ними. С этой целью полученные показатели работы долот в обоих вариантах бурения были обработаны методами математической статистики, описанной в главе IV. В результате этого данные, содержащие грубые ошибки, исключались из рассмотрения и не вошли в табл.
43. При этом было установлено, что средняя проходка на трехшарошечное долото Б-269С при бурении с кривыми переводниками с углом смещения осей резьб 2 и 2,5° составляет соответственно 30,7 и 24,4 м исправленное среднемвадратичбское отклонение 10,0 и 7,26 м коэффициент вариации 32,6 и 27,5% точность 2,70 и 1,67 м при вероятности 0,80.
[c.184]
Уровень колеблемости показателей по НГДУ определяют с помощью среднеквадратичного отклонения, дисперсии и коэффициента вариации. Так, степень колеблемости уровня производительности труда по выборочной совокупности НГДУ по отношению к среднему показателю можно оценить с помощью среднеквадратичного отклонения в абсолютных единицах а и коэффициента вариации V в процентах по формулам [c.86]
Показатели Среднее значение Среднее квадрати-ческое отклонение Коэффициент вариации [c.26]
Данные, приведенные в табл. 15, показывают, что факторы, характеризующие уровень затрат подсистемы, имеют значительную колеблемость, которая обусловлена главным образом факторами природно-геологичес-кого характера.
Вместе с этим некоторые факторы с высокой колеблемостью зависят от производственной деятельности коллектива и поэтому в большей степени, чем природные факторы, поддаются регулированию. k ним относятся такие показатели, как давление закачки на устье скважин (коэффициент вариации составляет 21,1%), удельный вес сточных вод в общем объеме закачки (коэффициент вариации равен 83 %). Высокая колеблемость этих факторов свидетельствует о больших возможностях снижения затрат на этом участке процесса добычи нефти. 38
[c.38]
Показатели Среднее значение Среднее квадратичес-кое отклоне- Коэффициент вариации Коэффициент частной Г-критерий [c.40]
Показатель Среднее значение Среднеквадра-тическое отклонение Дисперсия Коэффициент вариации [c.83]
Для сравнения НГДУ лучшим показателем является коэффициент вариации (четвертая строка, табл. 27). Особенно отличается НГДУ по средним дебитам на отработанный скважино-месяц (в среднем 66,4%), временем эксплуатации (54%), фондоемкостью на одну
[c.
91]
Для сравнения НГДУ лучшим показателем является коэффициент вариации (четвертая строка, табл. 31). Особенно отличается НГДУ по средним процентам обводненности нефти (в среднем 43,61%), времени эксплуатации (53,08%), фондоемкости на одну скважину (29,72%). Как следствие большой вариации факторов, наблюдается заметная вариация и уровня себестоимости добычи нефти и газа (18,4%). Силу связи между вариациями себестоимости добычи нефти и газа и факторов вскрывают частные коэффициенты корреляции. Наиболее сильно коррелируют с себестоимостью добычи нефти и газа обводненность нефти (0,52), средний дебит (0,38), время (0,14), а наиболее слабо — фондоемкость на одну скважину эксплуатационного фонда (0,1). [c.96]
Во-вторых, основными показателями оценки риска на рынке капитала являются дисперсия и среднее квадратическое отклонение. Распространенность и пригодность в сравнительном анализе этих статистик в данном случае объясняется тем обстоятельством, что базисным показателем при расчетах является доходность, т.
е. относительный показатель, сопоставимый как в динамике, так и по различным видам активов. Поэтому независимо от анализируемых активов соответствующие им показатели доходности и дисперсии однопорядковы и нет острой необходимости применять в оценке коэффициент вариации.
[c.85]
Критерием однородности информации служит среднеквадра-тическое отклонение и коэффициент вариации, которые рассчитываются по каждому факторному и результативному показателю. [c.141]
Минимальный размах колебаний, дисперсии, среднего квадрати-ческого отклонения и коэффициента вариации имеет депозитные ставки, а максимальный — ставки по кредитам. Это свидетельствует о том, что наиболее стабильными в анализируемом периоде являлись депозитные ставки, так как они имели наименьшую изменчивость в течение года. Наименьшая устойчивость в 1996 г. была присуща ставкам по кредитам, так как именно этим процентным ставкам соответствуют самые высокие уровни показателей вариации. [c.607]
Коэффициент вариации КЙ представляет собой процентное отношение сред-неквадратического отклонения к среднеарифметическому значению отчетного показателя (например, прибыли)
[c.
322]
При расчете относительных показателей вариации базой для сравнения служит средняя арифметическая. Эти показатели вычисляются как отношение размаха среднелинейного отклонения или средне-квадратического отклонения к средней арифметической. Чаще всего они выражаются в процентах или относительных величинах и определяют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 0,3, или 30% (для распределений, близких к нормальному). Различают следующие относительные показатели вариации (У) [c.66]
Необходимость расчета показателей вариации — Мегаобучалка
Средняя представляет собой обобщающую статистическую характеристику, в которой получает количественное выражение типичный уровень признака, которым обладают члены изучаемой совокупности. Но одной средней нельзя отобразить все характерные черты статистического распределения. Возможны случаи совпадения средних арифметических при разном характере распределения.
Показатели вариации используются для характеристики и упорядочения статистических совокупностей.
Абсолютные показатели вариации
Для измерения размера вариации используются следующие абсолютные показатели: размах, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение.
Размах
Величина его целиком зависит от случайности распределения крайних членов ряда, и значение подавляющего большинства членов ряда не учитывается, в то время как вариация связана с каждым значением члена ряда.
Такие показатели, которые представляют собой средние, полученные из отклонений индивидуальных значений признака от их средней величины, лишены этого недостатка.
Между индивидуальными отклонениями от средней и колеблемостью конкретного признака существует прямая зависимость. Чем сильнее колеблемость, тем больше абсолютные размеры отклонений от средней.
Дисперсия
Среднее линейное отклонение
Среднее квадратическое отклонение
Дисперсию можно подсчитать и по следующей формуле:
По этой формуле ленче считать дисперсию, когда имеешь дело с дискретным рядом распределения.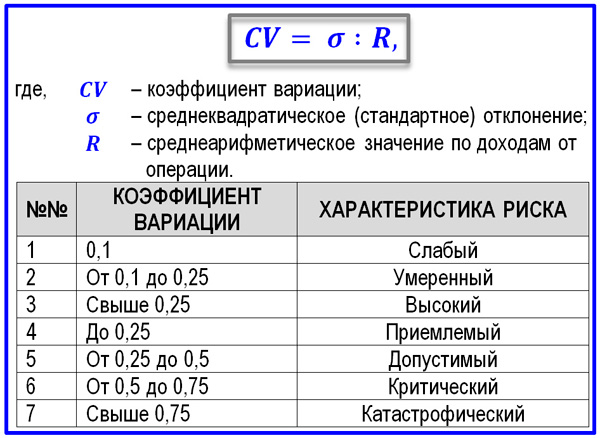
| Годовой удой от одной коровы | Середина интервала | Число коров | |||||
| до 2-х | 1,5 | 40 | 6 | -1,3 | 5,2 | 1,69 | 6,76 |
| 2-3 | 2,5 | 20 | 5 | -0,3 | 0,6 | 0,09 | 0,18 |
| 3-4 | 3,5 | 20 | 7 | +0,7 | 1,4 | 0,49 | ,98 |
| 4-5 | 4,5 | 10 | 4,5 | +1,7 | 1,7 | 2,89 | 2,89 |
| 5 и более | 5,5 | 10 | 5,5 | +2,7 | 2,7 | 7,29 | 7,29 |
| Сумма | 28 | 11,6 | 18,1 |
Относительные показатели вариации
Коэффициент осцилляции –
Коэффициент относительного линейного отклонения –
Коэффициент вариации–
Дисперсия альтернативного признака
Альтернативный признак – это такой признак, которым одни члены обладают, а другие – нет.
доля единиц, не обладающих признаком
доля единиц, обладающих признаком
Виды дисперсий и правила их сложения
Межгрупповая дисперсия
Между отдельными видами дисперсий существует взаимосвязь, которую можно записать в виде правила сложения дисперсий:
Пример: Распределение сотрудников КБ по производительности труда
Расчет общей дисперсии
| x | f | xf | x2 | x2f |
| 10 | 50 | 50 | 100 | 500 |
| 11 | 150 | 165 | 121 | 1815 |
| 13 | 50 | 65 | 169 | 845 |
| 15 | 50 | 75 | 225 | 1125 |
| 18 | 70 | 126 | 324 | 2268 |
| 20 | 30 | 60 | 400 | 1200 |
| 40 | 541 | 7753 |
2.
Расчет дисперсии по первой группе
| x | f | xf | x2 | x2f |
| 10 | 50 | 50 | 100 | 500 |
| 11 | 150 | 165 | 121 | 1815 |
| 13 | 50 | 65 | 169 | 845 |
| 25 | 280 | 3160 |
3. Расчетдисперсии по второй группе
| x | f | xf | x2 | x2f |
| 15 | 50 | 75 | 225 | 1125 |
| 18 | 70 | 126 | 324 | 2268 |
| 20 | 30 | 60 | 400 | 1200 |
| 15 | 261 | 4593 |
4.
Расчет межгрупповой дисперсии
| 11,2 | 25 | -2,325 | 5,405 | 135,140 |
| 17,4 | 15 | 3,875 | 15,015 | 225,234 |
| 40 | 360,375 |
5. Расчет средней из индивидуальных дисперсий
Эмпирическое корреляционное отношение (ЭКО)
На основании правила сложения дисперсий вычисляется эмпирическое корреляционное отношение (ЭКО), которое равно квадратному корню из отношения межгрупповой дисперсии к общей:
Такой порядок вычисления обусловлен разложением общей вариации на вариацию, зависящую от фактора, положенного в основу группировки (в нашем примере – повышение и неповышение квалификации), которая численно равна межгрупповой дисперсии, и общую вариацию.
Межгрупповая дисперсия составляет часть общей дисперсии и складывается под влиянием только одного группировочного фактора. Именно поэтому подкоренное выражение показывает долю вариации за счет группировочного признака.
ЭКО изменяется в переделах от нуля до единицы. Чем ближе его значение к единице, тем большая доля вариации падает на группировочный признак.
В нашем случае
Некоторые математические свойства дисперсий
(1) При вычитании из всех значений признака некоторой постоянной величины дисперсия не изменится.
(2) При сокращении всех значений на постоянный множитель дисперсия уменьшится в раз.
(3) Средний квадрат отклонений значений признака от постоянной произвольной величины больше дисперсии признака на квадрат разности между средней арифметической и постоянной величиной .
На основании свойств дисперсии ее можно подсчитать способом отсчета от условного нуля и способом моментов.
| Интервал | ||||||||
| 90-100 | 95 | 2 | 190 | -30 | -3 | -6 | 9 | 18 |
| 100-110 | 105 | 6 | 630 | -20 | -2 | -12 | 4 | 24 |
| 110-120 | 115 | 8 | 920 | -10 | -1 | -8 | 1 | 8 |
| 120-130 | 125 | 18 | 2 250 | 0 | 0 | 0 | 0 | 0 |
| 130-140 | 135 | 5 | 675 | 10 | 1 | 5 | 1 | 5 |
| 140-150 | 145 | 4 | 580 | 20 | 2 | 8 | 4 | 16 |
| 150-160 | 155 | 3 | 465 | 30 | 3 | 9 | 9 | 27 |
| 160-170 | 165 | 2 | 330 | 40 | 4 | 8 | 16 | 32 |
| 170-180 | 175 | 2 | 350 | 50 | 5 | 10 | 25 | 50 |
| 50 | 6 390 | 14 | 180 |
Экономические индексы
Понятие индексов
В статистике под индексом понимается относительная величина (показатель), выражающая изменение сложного экономического явления во времени, в пространстве или по сравнению с планом. В связи с этим различают динамические, территориальные индексы, а также индексы выполнения плана.
Многие общественные явления состоят из непосредственно несопоставимых явлений, поэтому основной вопрос – это вопрос сопоставимости сравниваемых явлений.
К какому бы экономическому явлению ни относились индексы, чтобы рассчитать их, необходимо сравнивать различные уровни, которые относятся либо к различным периодам времени, либо к плановому заданию, либо к различным территориям. В связи с этим различают базисный период (период, к которому относится величина, подвергаемая сравнению) и отчетный период (период, к которому относится сравниваемая величина). При исчислении важно правильно выбрать период, принимаемый за базу сравнения.
Индексы могут относиться либо к отдельным элементам сложного экономического явления, либо ко всему явлению в целом.
Онлайн калькулятор показателей вариации
Следующий онлайн калькулятор способен сделать расчет показателей вариации, а именно расчет дисперсии, размаха вариации, среднего отклонения и не только.
Вариацией называют различие значений по какому-нибудь признаку в середине совокупности, которая в данный момент есть объектом изучения.
Приведем пример, представьте класс учеников — они и есть объект изучения, все они учат английский язык. Берем статистику за весь год (табель) и смотрим. Кто-то знает предмет на 5, кто-то на 4, а еще некоторые на 3. Так вот вариация и есть различие в оценках, приведенная к количеству человек, то есть 10 школьников знают на 5, 8 знают на 4, и например 5 знают на 3. В данном случае количество человек с определенной оценкой в классе называется частотой и встречаемостью вариации.
The field is not filled.
‘%1’ is not a valid e-mail address.
Please fill in this field.
The field must contain at least% 1 characters.
The value must not be longer than% 1 characters.
Field value does not coincide with the field ‘%1’
An invalid character. Valid characters:’%1′.
Expected number.
It is expected a positive number.
Expected integer.
It is expected a positive integer.
The value should be in the range of [%1 .. %2]
The ‘% 1’ is already present in the set of valid characters.
The field must be less than 1%.
The first character must be a letter of the Latin alphabet.
Su
Mo
Tu
We
Th
Fr
Sa
January
February
March
April
May
June
July
August
September
October
November
December
century
B.C.
%1 century
An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3
Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).
%3.%2.%1%4
%3.%2.%1%4 %6:%7
s.sh.
u.sh.
v.d.
z.d.
yes
no
Wrong file format. Only the following formats: %1
Please leave your phone number and / or email.
minutes
minutes
minute
minutes
minutes
minutes
minutes
minutes
minutes
minutes
minutes
minutes
minutes
hour
hours
hours
hours
hours
hours
hours
hours
hours
hours
hours
days
day
day
day
day
days
days
days
days
days
days
days
month
month
month
month
months
months
months
months
months
months
months
year
of the year
of the year
of the year
years
years
years
years
years
years
years
ago
%1 minutes ago
%1 minutes ago
%1 minutesу ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 hour ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 days ago
%1 day ago
%1 day ago
%1 day ago
%1 day ago
%1 days ago
%1 days ago
%1 days ago
%1 days ago
%1 days ago
%1 days ago
%1 days ago
%1 month ago
%1 month ago
%1 month ago
%1 month ago
%1 months ago
%1 months ago
%1 months ago
%1 months ago
%1 months ago
%1 months ago
%1 months ago
%1 year ago
%1 of the year ago
%1 of the year ago
%1 of the year ago
%1 years ago
%1 years ago
%1 years ago
%1 years ago
%1 years ago
%1 years ago
%1 years ago
Показатели вариацииСреднее арифметическое:
Размах вариации:
Среднее линейное отклонение:
Среднее квадратическое отклонение:
Коэффициент осцилляции (проценты):
Относительное линейное отклонение (проценты):
Коэффициент вариации (проценты):
Калькулятор стандартного отклонения сгруппированных данныхРешенный пример проблемы
Этот решенный ниже пример задачи для стандартного отклонения частотного распределения может помочь пользователям понять, как значения используются для тренировки такого расчета на основе приведенных выше математических формул.
Пример задачи:
В классе учеников 9 учеников набрали от 50 до 60, 7 учеников набрали от 61 до 70, 9 учеников получили от 71 до 85, 12 учеников получили от 86 до 95 и 8 учеников получили от 96 до 100 по предмету математика.Оценить стандартное отклонение?
Решение:
Ввод:
| Диапазон | Частота |
| 50-60 | 9 |
| 61-70 | 7 |
| 71-85 | 9 |
| 86-95 | 12 |
| 96-100 | 8 |
шаг 1: найти среднюю точку M для каждой группы
(50 + 60) / 2 = 55
(61 + 70) / 2 = 65.5
(71 + 85) / 2 = 78
(86 + 95) / 2 = 90,5
(96 + 100) / 2 = 98
Средние баллы составляют 55, 65,5, 78, 90,5 и 98 для группы студентов От 50 до 60, от 61 до 70, от 71 до 85, от 86 до 95 и от 96 до 100 соответственно.
шаг 2: вычислить количество выборок n
n = 9 + 7 + 9 + 12 + 8
n = 45
шаг 3: найти среднее значение сгруппированных данных μ
μ = (55 x 9 + 65,5 x 7 + 78 x 9 + 90,5 x 12 + 98 x 8) / n
= 3525,5 / 45
μ = 78.3444
шаг 4: найти дисперсию σ 2
= (((9 x 552) + (7 x 65,52) + (9 x 782) + (12 x 90,52) + (8 x 982)) — (45 x 78,3444 2 )) / (45 — 1)
= (287127,75 — 276203,025) / 44
σ 2 = 248,2820
шаг 5: найти стандартное отклонение для сгруппированных данных
Возьмите квадрат корень дисперсии
σ = 15,7569
Стандартное отклонение, сгруппированное по функции , используется в различных приложениях для статистического анализа данных.Когда дело доходит до онлайн, этот сгруппированный калькулятор стандартного отклонения вместе с формулой, пошаговым расчетом и решенным примером задачи позволяет пользователям понимать, тренировать, выполнять и проверять такие вычисления.
Калькулятор отклонения| Определение и формула
Пример расчета
Давайте посчитаем дисперсию оценок восьми студентов в викторине: 5, 5, 5, 7, 8, 8, 9, 9 . Выполните следующие шаги:
1. Рассчитайте среднее значение
Чтобы вычислить среднее значение (x), разделите сумму всех чисел на количество точек данных:
x̄ = (5 + 5 + 5 + 7 + 8 + 8 + 9 + 9) / 8
х = 7
2.Вычислите разницу от среднего значения и квадраты разностей от среднего
Теперь, когда мы знаем, что среднее значение равно 7 , мы вычислим разницу от среднего по формуле:
x i - x̄
Первая точка имеет значение 5 , поэтому разница от среднего составляет 5-7 = -2 .
Квадрат разницы (или «квадратичное отклонение») от среднего — это просто квадрат предыдущего шага:
(x i - x̄) 2
, поэтому квадрат отклонения будет:
(5-7) 2 = (-2) 2 = 4
Мы показываем рассчитанные квадраты отклонений от среднего для всех результатов викторины в таблице ниже.Столбец «Отклонение от среднего» — это результат минус 7, а столбец «Квадратное отклонение» — это квадрат предыдущего столбца.
| Гол | Отклонение от среднего | Квадратное отклонение |
|---|---|---|
| 5 | -2 | 4 |
| 5 | -2 | 4 |
| 5 | -2 | 4 |
| 7 | 0 | 0 |
| 8 | 1 | 1 |
| 8 | 1 | 1 |
| 9 | 2 | 4 |
| 9 | 2 | 4 |
3.Вычислить дисперсию и стандартное отклонение
Затем мы используем квадраты отклонений от среднего, найденного на шаге 2 в уравнении дисперсии:
σ 2 = ∑ (x i - x̄) 2 / N
σ 2 = (4 + 4 + 4 + 0 + 1 + 1 + 4 + 4) / 8
σ 2 = 2,75
Дисперсия результатов теста составила 2,75 .
Обратите внимание, что если бы мы использовали выборочные данные для оценки дисперсии генеральной совокупности, мы бы вместо этого использовали уравнение выборочной дисперсии:
с 2 = ∑ (x i - x̄) 2 / (N - 1)
Теперь, когда вы знаете, как найти дисперсию, попробуйте вычислить ее самостоятельно, а затем проверьте свой ответ с помощью нашего калькулятора!
Коэффициент вариации Пример вопроса | CFA, уровень I
Коэффициент вариации CV — это мера разброса, которая описывает степень изменчивости данных относительно их среднего значения.Он не имеет единиц , и поэтому мы можем использовать его в качестве альтернативы стандартному отклонению для сравнения изменчивости наборов данных с разными средними значениями.
Формула коэффициента вариации
$$ \ text {CV} = \ cfrac {S} {\ text x̄} $$
Где S — стандартное отклонение выборки
А x — среднее значение выборки.
Примечание. Формулу можно заменить на σ / μ при работе с генеральной совокупностью.
Порядок расчета коэффициента вариации:
- Вычислить среднее значение данных.
- Рассчитайте стандартное отклонение выборки набора данных, S.
- Найдите отношение S к среднему, x̄.
Пример: расчет коэффициента вариации
Рассчитайте относительную изменчивость для выборок 40, 46, 34, 35 и 45 популяции.
Решение
Шаг 1: Рассчитайте среднее значение.
$$ \ text {Среднее} = \ cfrac {(40 + 46 + 34 + 35 + 45)} {5} = \ cfrac {200} {5} = 40 $$
Шаг 2: Рассчитайте стандартное отклонение выборки.2 }} {4} \\ & = \ cfrac {122} {4} \\ & = 30,5 \\ \ end {align *} $$
Примечание. Поскольку это стандартное отклонение выборки, а не стандартное отклонение генеральной совокупности, мы используем n — 1 в качестве знаменателя.
Следовательно,
$$ S = \ sqrt {30.5} = 5.52268 $$
Шаг 3 : Рассчитайте коэффициент.
$$ \ text {Ratio} = \ cfrac {5.52268} {40} = 0.13806 \ text {или} 13.81 \% $$
(Кандидаты могут использовать эти ссылки, чтобы обновить свою память при вычислении среднего и стандартного отклонения)
Интерпретация коэффициента вариации
В финансах коэффициент вариации используется для измерения риска на единицу прибыли .Например, предположим, что средняя месячная доходность казначейских векселей составляет 0,5% со стандартным отклонением 0,58%. Предположим, у нас есть еще одна инвестиция, скажем, Y со средней месячной доходностью 1,5% и стандартным отклонением 6%. Затем
$$ \ text {CV} _ {\ text T- \ text {Bill}} = \ cfrac {0.58} {0.5} = 1.16 $$
$$ \ text {CV} _ \ text {Y} = \ cfrac {6} {1.5} = 4 $$
Интерпретация: Разброс на единицу ежемесячной доходности казначейских векселей меньше, чем у Y. Следовательно, вложение Y более рискованно, чем вложение в казначейские векселя.
Вопрос
Если средняя ожидаемая доходность ценной бумаги составляет 10%, а стандартное отклонение — 5%, коэффициент вариации составляет , ближайший к:
А. 0,5
Б. 2
К. 0,005
Решение
$$ \ text {CV} = \ cfrac {S} {\ text x̄} = \ cfrac {0.05} {0.10} = 0.5 $$
Где S — стандартное отклонение выборки
А x — среднее значение выборки.
Чтение 7 LOS 7i
Рассчитайте и интерпретируйте коэффициент вариации.
.