Сегмент круга это: Онлайн калькулятор: Сегмент круга

Круг: сектор, сегмент. Площадь круга, сектора и сегмента

Круг — это часть плоскости, ограниченная окружностью. Центр данной окружности называется центром круга, а расстояние от центра до любой точки окружности — радиусом круга:

O  — центр круга,  OA  — радиус круга.

Площадь круга

Площадь круга равна произведению числа  π  на квадрат радиуса. Формула нахождения площади круга:

S = πr²,

где  S  — площадь круга, а  r  — радиус круга.

Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:

D = 2r,   значит   r =	D	.
	2

Следовательно, формула нахождения площади круга через диаметр будет выглядеть так:

S  =  π(	D	)2  =  π	D2	=  π	D2	.
	2		22		4

Сектор круга. Площадь сектора

Сектор — это часть круга, ограниченная двумя радиусами и дугой. Два радиуса разделяют круг на два сектора:

Чтобы найти площадь сектора, дуга которого содержит  n°,  надо площадь круга разделить на  360  и полученный результат умножить на  n.

Формула площади сектора:

S =	πr2	· n =	πr2n	,
	360		360

где  S  — площадь сектора. Выражение

можно представить в виде произведения

πr2n	= n ·	πr	·	r	,
360		180		2

где	nπr	— это длина дуги сектора.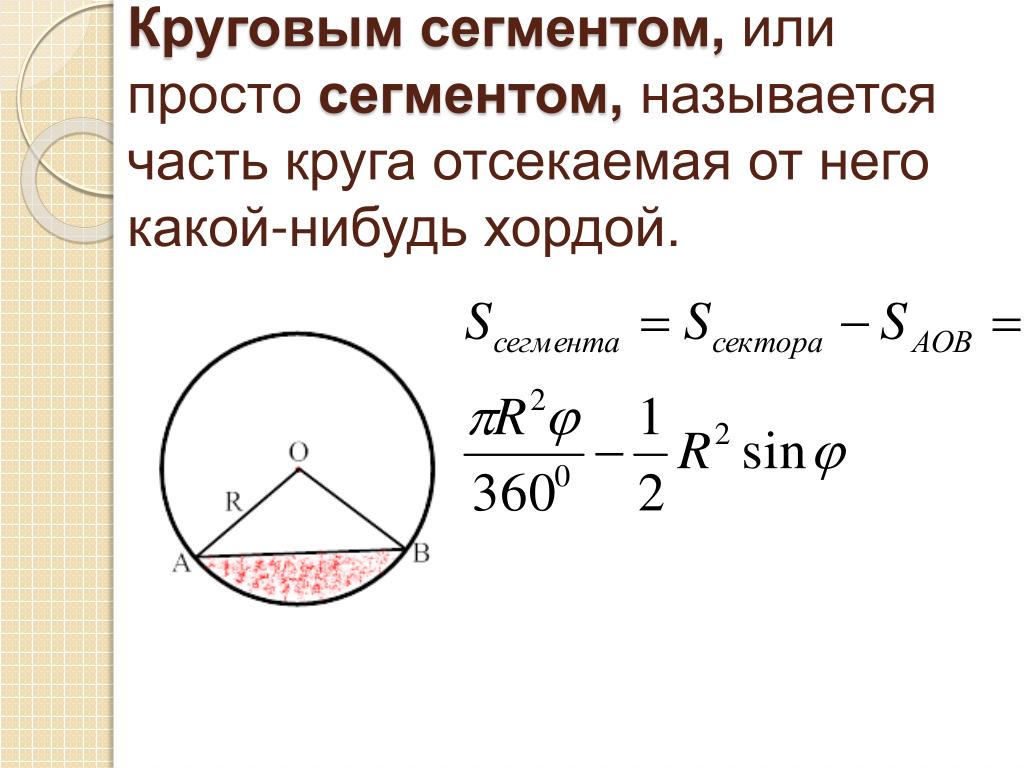
	180

Следовательно, площадь сектора равна длине дуги сектора, умноженной на половину радиуса:

где  S  — это площадь сектора,  s  — длина дуги данного сектора,  r  — радиус круга.

Сегмент. Площадь сегмента

Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой. Любая хорда делит круг на два сегмента:

Площадь сегмента равна половине радиуса, умноженной на разность между дугой сегмента и половиной хорды двойной дуги.

Площадь сегмента  AMB  будет вычисляться по формуле:

где  S  — это площадь сегмента,  r  — радиус круга,  s  — длина дуги  AB,  а  BC  — длина половины хорды двойной дуги.

формулы через радиус и угол сектора

В данной публикации мы рассмотрим определение сегмента круга и формулы, с помощью которых можно вычислить его площадь (через радиус и центральный угол кругового сектора). Также разберем примеры решения задач для демонстрации практического применения формул.

Определение сегмента круга

Сегмент круга – это часть круга, которая ограничена дугой окружности и ее хордой.

Хорда – это часть прямой (секущей), которая пересекает круг. Концы хорды соединяются с центром круга, в результате чего образуется равнобедренный треугольник, боковые стороны которого являются радиусом окружности. Если к этом треугольнику добавить сегмент, получится сектор.

На рисунке выше:

• сегмент круга закрашен зеленым цветом;
• отрезок AB – это хорда;
• часть окружности между точками AB – дуга окружности;
• R – радиус круга;
• α – угол сектора.

Формулы нахождения площади кругового сегмента

Через радиус и центральный угол в градусах

α° – угол в градусах.

Примечание: в расчетах используется значение π, приблизительное равное числу 3,14.

Через радиус и угол сектора в радианах

α_рад – угол в радианах.

Примеры задачи

Задание 1
Найдите площадь сегмента круга, если его радиус равен 8 см, а центральный угол сектора, стягивающего сегмент, составляет 45 градусов.

Решение
Воспользуемся первой формулой, подставив в нее известные значения:

Задание 2
Площадь кругового сегмента составляет 24 см², а центральный угол сектора круга, частью которого является сегмент, равняется 1 радиану. Найдите радиус круга.

Решение
В данном случае мы можем получить радиус из формулы, в которой задействован угол в радианах:

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

Основные определения и свойства

Фигура	Рисунок	Определения и свойства
Окружность		Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности
Дуга		Часть окружности, расположенная между двумя точками окружности
Круг		Конечная часть плоскости, ограниченная окружностью
Сектор		Часть круга, ограниченная двумя радиусами
Сегмент		Часть круга, ограниченная хордой
Правильный многоугольник		Выпуклый многоугольник, у которого все стороны равны и все углы равны
		Около любого правильного многоугольника можно описать окружность

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Дуга

Часть окружности, расположенная между двумя точками окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Сектор

Часть круга, ограниченная двумя радиусами

Сегмент

Часть круга, ограниченная хордой

Правильный многоугольник

Выпуклый многоугольник, у которого все стороны равны и все углы равны Около любого правильного многоугольника можно описать окружность

      Определение 1. Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.

      Определение 2. Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.

      Замечание 1. Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.

      Определение 3. Числом π (пи) называют число, равное площади круга радиуса 1.

      Замечание 2. Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:

      Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.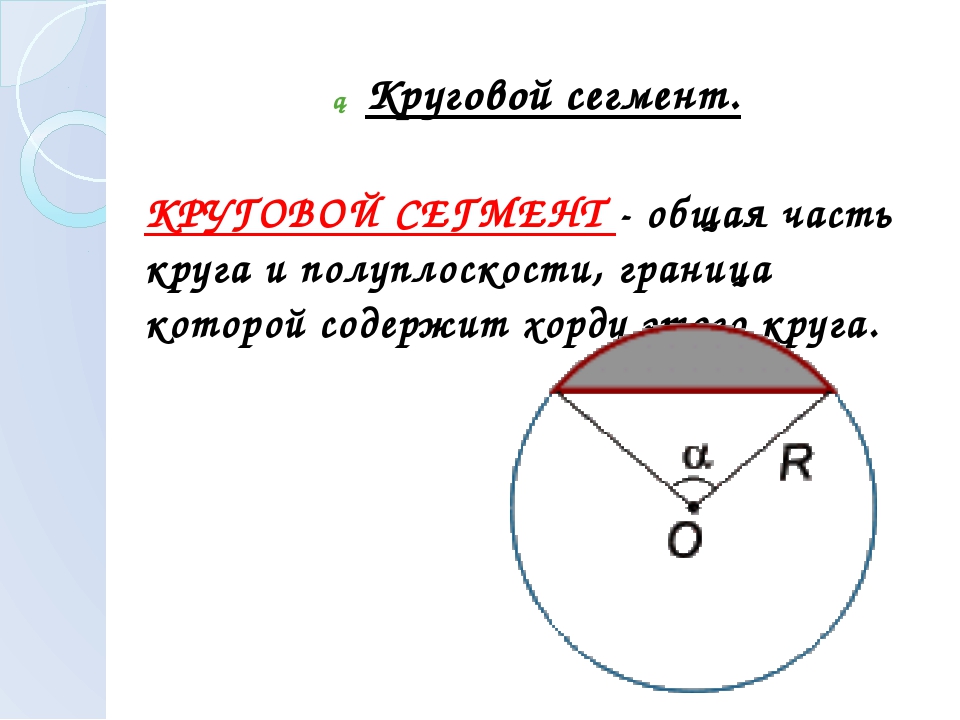

Формулы для площади круга и его частей

Формулы для длины окружности и её дуг

Площадь круга

      Рассмотрим две окружности с общим центром (концентрические окружности) и радиусами радиусами 1 и R, в каждую из которых вписан правильный   n – угольник (рис. 1).

      Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1.

Рис.1

      Площадь правильного n – угольника, вписанного в окружность радиуса R, равна

      Площадь правильного n – угольника, вписанного в окружность радиуса 1, равна

      Следовательно,

      Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1, стремится к π, то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R, стремится к числу   πR².

      Таким образом, площадь круга радиуса R, обозначаемая S, равна

S = πR².

Длина окружности

      Рассмотрим правильный   n – угольник   B₁B₂…B_n , вписанный в окружность радиуса радиуса R, и опустим из центраO окружности перпендикуляры на все стороны многоугольника (рис. 2).

Рис.2

      Поскольку площадь n – угольника   B₁B₂…B_n   равна

то, обозначая длину окружности радиуса R буквой C, мы, в соответствии с определением 2, при увеличении n получаем равенство:

откуда вытекает формула для длины окружности радиуса R:

C = 2πR.

      Следствие. Длина окружности радиуса 1 равна   2π.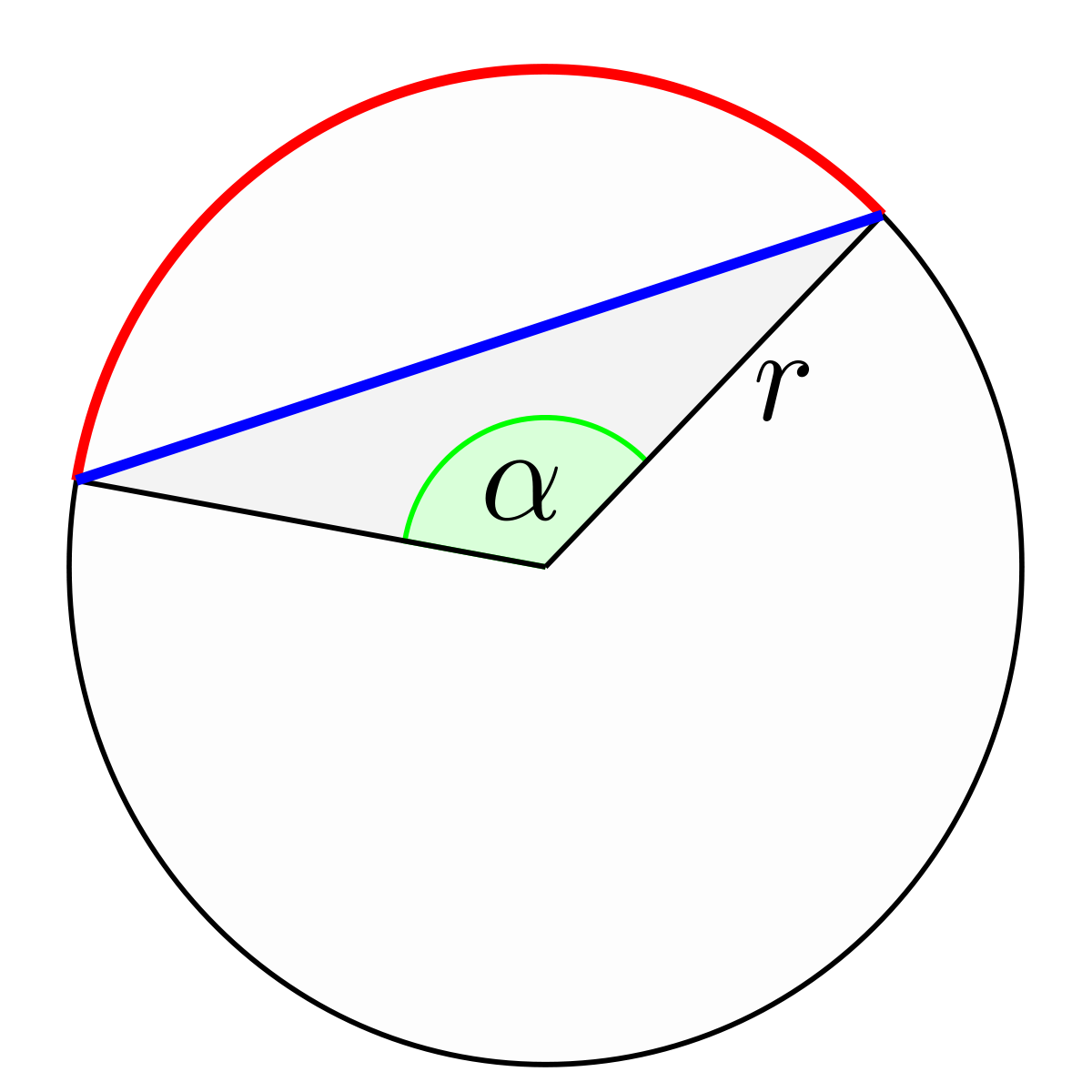

Длина дуги

      Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.

Рис.3

      В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

      В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сектора

      Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.

Рис.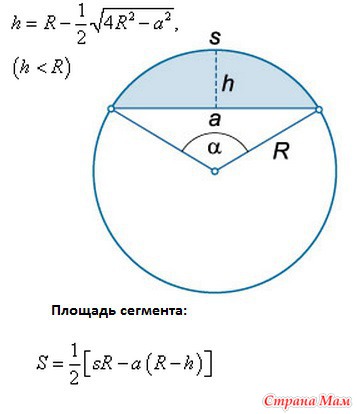 4

      В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

      В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сегмента

      Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.

Рис.5

      Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем

      Следовательно,

      В случае, когда величина α выражена в в радианах, получаем

      Следовательно,

      На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.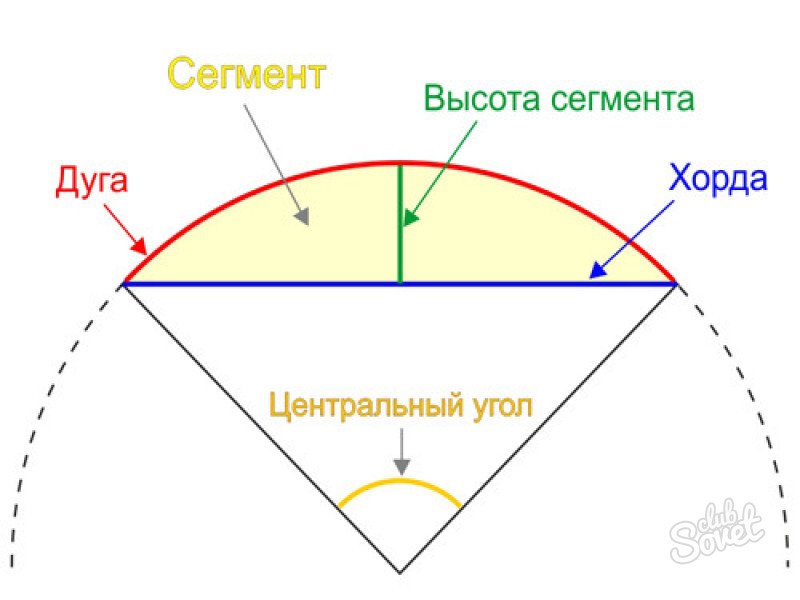

Программа вычисления параметров сегмента круга

30.06.2012 // Владимир Трунов   

Программа Segment предназначена для вычисления геометрических параметров сегмента круга. В расчетах участвуют пять величин:

• диаметр круга,
• длина дуги,
• длина хорды,
• центральный угол,
• высота сегмента,

любые две из которых задаются, а оставшиеся вычисляются.

Дополнительно вычисляются значения:

• длины окружности,
• площади круга,
• площади сегмента,
• площади сектора,

соответствующие заданным величинам.

Теоретическая сторона вычислений описана в статье Геометрия круга.

Программа очень пригодится людям, проектирующим что-нибудь круглое. Например, ювелирам для разработки эскизов колец, браслетов и прочей ерунды.

Segment рассчитана на выполнение под Windows (XP, 7, 8, 10) и не требует специальной установки. Нужно просто извлечь из архива два файла и поместить их в одну папку.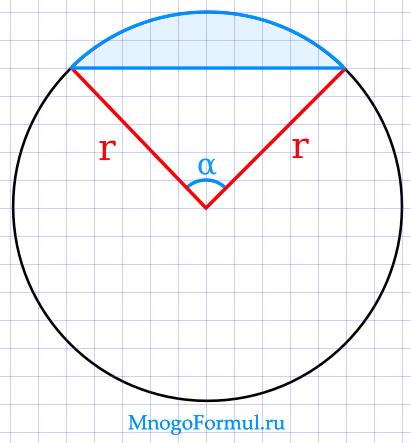

• Segment.exe — выполняемый файл;
• SegmentHelp.chm — файл справки, который открывается не только из программы, но и отдельно, так что вы можете изучить его еще до запуска программы.

Для удаления программы — просто удалить эти файлы.

Программа распространяется бесплатно и не содержит рекламы.

Примечание 1. Если у программы возникнут проблемы с системой безопасности Windows, то обратитесь к статье Как скачать программу.

Примечание 2. Если при запуске программы вы получаете сообщение, содержащее название .NET Framework, то обратитесь к статье Что такое .NET Framework.

Примечание 3. Если вы скачали программу, то настоятельно советую вам подписаться на рассылку «Новости сайта tvlad.ru» (форма в правой колонке). Здесь нет никакого подвоха, поскольку для вас в этом — никакого урона, а для меня — никакой прибыли. Просто это единственный способ для вас оперативно узнать о выходе новых версий программы, которую вы скачали.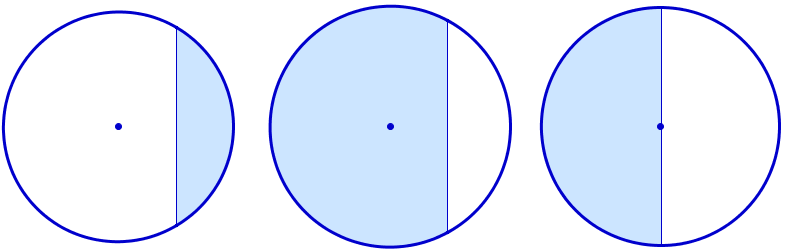

Окружность, круг, сегмент, сектор. Формулы и свойства

Определение. Окружность — это совокупность всех точек на плоскости, которые находятся на одинаковом расстоянии от заданной точки О, которая называется центром окружности.

Определение. Единичная окружность — окружность, радиус которой равна единице.

Определение. Круг — часть плоскости, ограничена окружностью.

Определение. Радиус окружности R — расстояние от центра окружности О до любой точки окружности.

Определение. Диаметр окружности D — отрезок, который соединяет две точки окружности и проходит через ее центр.

Основные свойства окружности

1. Диаметр окружности равен двум радиусам.

D = 2r

2. Кратчайшее расстояние от центра окружности к секущей (хорде) всегда меньше радиуса.

3. Через три точки, которые не лежат на одной прямым, можно провести только одну окружность.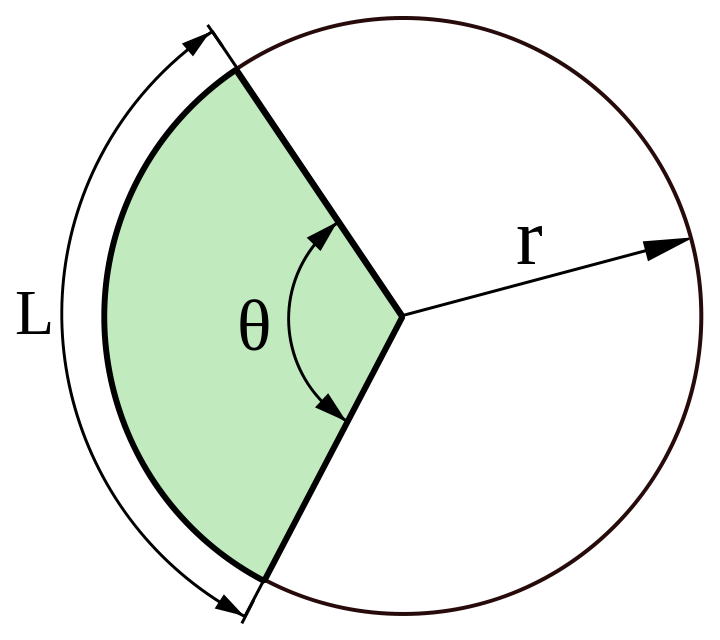

4. Среди всех замкнутых кривых с одинаковой длиной, окружность имеет наибольшую площадь.

5. Если две окружности соприкасаются в одной точке, то эта точка лежит на прямой, что проходит через центры этих окружностей.

Формулы длины окружности и площади круга

Формулы длины окружности

1. Формула длины окружности через диаметр:

L = πD

2. Формула длины окружности через радиус:

L = 2πr

Формулы площади круга

1. Формула площади круга через радиус:

S = πr²

2. Формула площади круга через диаметр:

S = πD²4

Уравнение окружности

1. Уравнение окружности с радиусом r и центром в начале декартовой системы координат:

r² = x² + y²

2. Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:

r² = (x — a)² + (y — b)²

3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:

{	x = a + r cos t
	y = b + r sin t

Касательная окружности и ее свойства

Определение.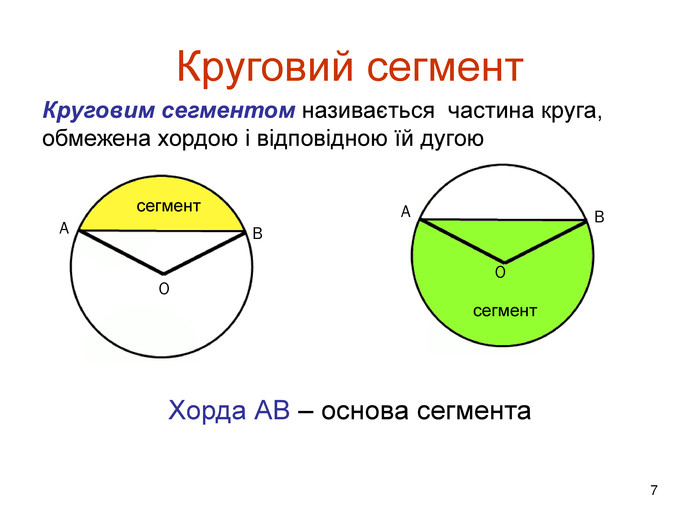

Касательная окружности — прямая, которая касается окружности только в одной точке.

Основные свойства касательных к окружности

1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.

2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.

3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:

AB = AC

Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:

∠ОAС = ∠OAB

Секущая окружности и ее свойства

Определение. Секущая окружности — прямая, которая проходит через две точки окружности.

Основные свойства секущих

1. Если с точки вне окружности (Q) выходят две секущие, которые пересекают окружность в двух точках A и B для одной секущей и C и D для другой секущей, то произведения отрезков двух секущих равны между собою:

AQ ∙ BQ = CQ ∙ DQ

2.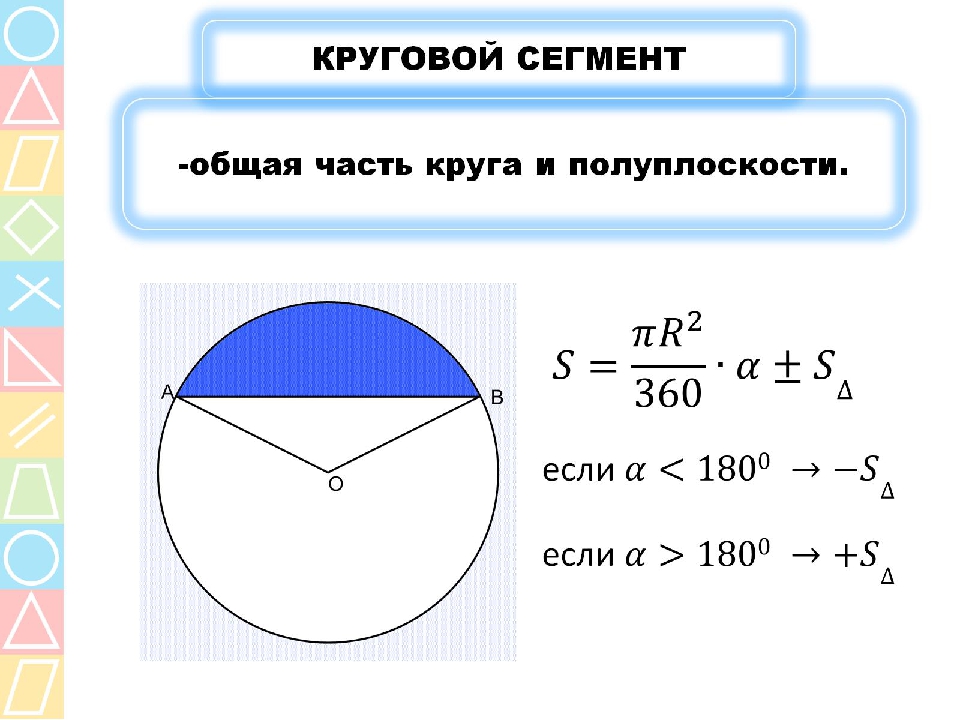 Если из точки Q вне окружности выходит секущая прямая, что пересекает окружность в двух точках A и B, и касательная с точкой соприкосновения C, то произведение отрезков секущей равна квадрату длины отрезка касательной:

AQ ∙ BQ = CQ²

Хорда окружности ее длина и свойства

Определение. Хорда окружности — отрезок, который соединяет две точки окружности.

Длина хорды

1. Длина хорды через центральный угол и радиус:

AB = 2r sin α2

2. Длина хорды через вписанный угол и радиус:

AB = 2r sin α

Основные свойства хорд

1. Две одинаковые хорды стягивают две одинаковые дуги:

если хорды AB = CD, то

дуги ◡ AB = ◡ CD

2. Если хорды параллельные, то дуги между ними будут одинаковые:

если хорды AB ∣∣ CD, то

◡ AD = ◡ BC

3. Если радиус окружности перпендикулярен к хорде, то он разделяет хорду пополам в точке их пересечения:

если OD ┴ AB, то

AC = BC

4. Если две хорды AB и CD пересекаются в точке Q, то произведение отрезков, что образовались при пересечении, одной хорды равны произведению отрезков другой хорды:

AQ ∙ BQ = DQ ∙ QC

5.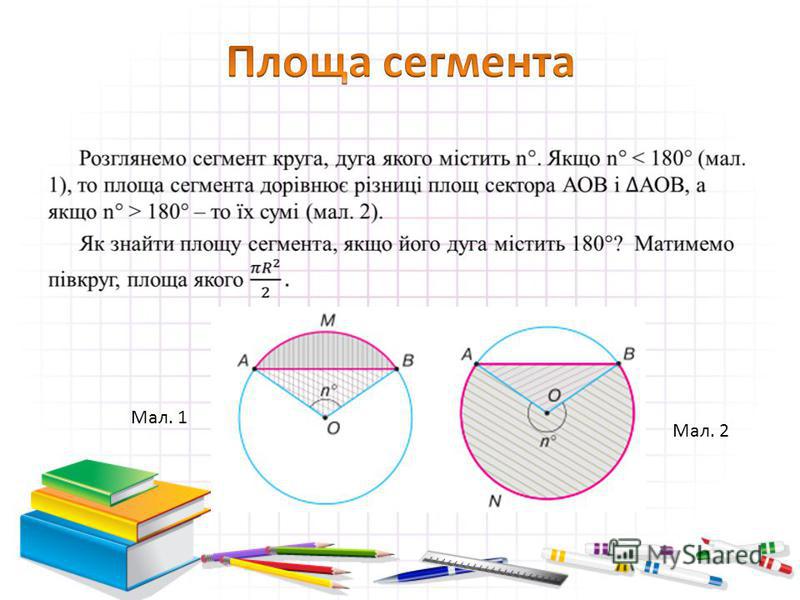 Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.

если хорды AB = CD, то

ON = OK

6. Чем больше хорда тем ближе она к центру.

если CD > AB, то

ON < OK

Центральный угол, вписанный угол и их свойства

Определение. Центральный угол окружности — угол, вершиной которого есть центр окружности.

Определение. Угол вписанный в окружность — угол, вершина которого лежит на окружности, а стороны угла пересекают окружность.

Основные свойства углов

1. Все вписанные углы, которые опираются на одну дугу — равны. 2. Вписанний угол, который опирается на диаметр будет прямым (90°). 3. Вписанный угол равен половине центрального угла, что опирается на ту же дугу

β = α2

4. Если два вписанных угла опираются на одну хорду и находятся по различные стороны от нее, то сумма этих углов равна 180°.

α + β = 180°

Определение. Дуга окружности (◡) — часть окружности, которая соединяет две точки на окружности.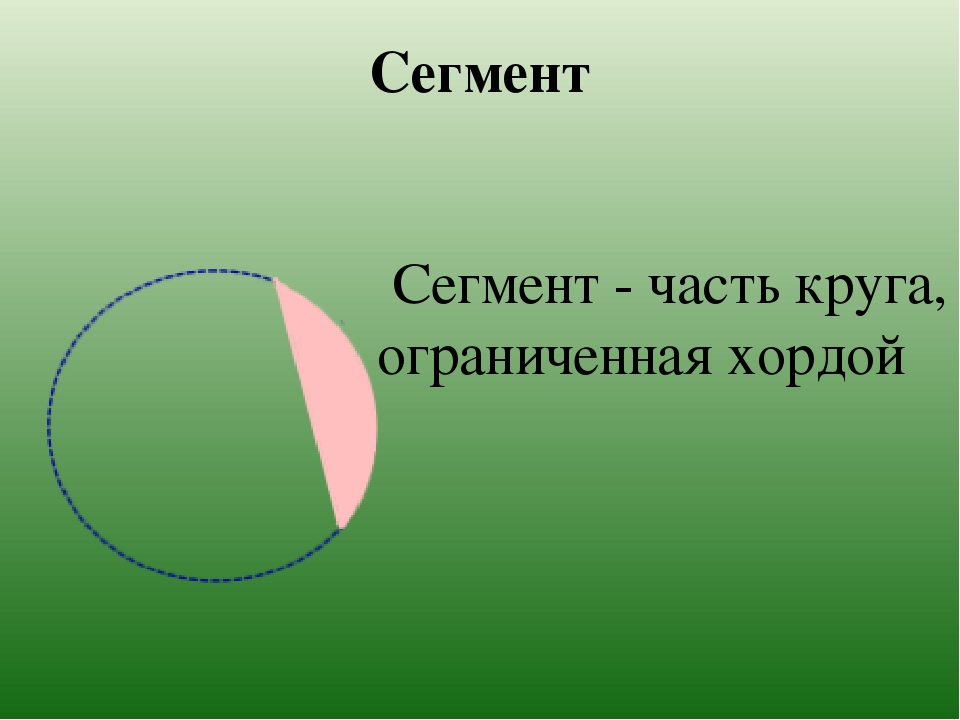

Определение. Градусная мера дуги — угол между двумя радиусами, которые ограничивают эту дугу. Градусная мера дуги всегда равна градусной мере центрального угла, который ограничивает эту дугу своими сторонами.

Формула длины дуги через центральный угол (в градусах):

l = πr180°∙ α

Определение. Полуокружность — дуга в которой концы соединены диаметром окружности.

Определение. Полукруг (◓) — часть круга, которая ограничена полуокружностью и диаметром.

Определение. Сектор (◔) — часть круга, которая ограничена двумя радиусами и дугой между этими радиусами.

Формула. Формула площади сектор через центральный угол (в градусах)

S = πr²360°∙ α

Определение. Сегмент — часть круга, которая ограничена дугой и хордой, что соединяет ее концы.

Определение. Концентрические окружности — окружности с различными радиусами, которые имеют общий центр.

Определение. Кольцо — часть плоскости ограниченная двумя концентрическими окружностями.

Сфера, шар, сегмент и сектор. Формулы и свойства

Определение.

Сфера (поверхность шара) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).

Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение.

Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).

Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение. Радиус сферы (шара) (R) — это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).

Определение. Диаметр сферы (шара) (D) — это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.

Формула. Объём шара: Формула. Площадь поверхности сферы через радиус или диаметр:

S = 4πR² = πD²

Уравнение сферы

1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат:

x² + y² + z² = R²

2. Уравнение сферы с радиусом R и центром в точке с координатами (x₀, y₀, z₀) в декартовой системе координат:

(x — x₀)² + (y — y₀)² + (z — z₀)² = R²

3. Параметрическое уравнение сферы с центром в точке (x₀, y₀, z₀):
x = x₀ + R · sin θ · cos φy = y₀ + R · sin θ · sin φz = z₀ + R · cos θ
где θ ϵ [0,π], φ ϵ [0,2π].

Определение. Диаметрально противоположными точками называются любые две точки на поверхности шара (сфере), которые соединены диаметром.

Основные свойства сферы и шара

1. Все точки сферы одинаково удалены от центра.

2. Любое сечение сферы плоскостью является окружностью.

3. Любое сечение шара плоскостью есть кругом.

4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.

5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара.

6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара.

7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.

8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются, а в плоскости пересечения образуется круг.

Секущая, хорда, секущая плоскость сферы и их свойства

Определение. Секущая сферы — это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.

Определение. Хорда сферы (шара) — это отрезок, соединяющий две точки сферы (поверхности шара).

Определение. Секущая плоскость — это плоскость, которая пересекает сферу.

Определение. Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или шара, сеченме образует соответственно большую окружность и большой круг. Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).

Любая хорда, проходящая через центр сферы (шара) является диаметром.

Хорда является отрезком секущей прямой.

Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:

d < R

Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:

m < R

Местом сечения секущей плоскости на сфере всегда будет малая окружность, а на шаре местом сечения будет малый круг. Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r такого круга можно найти по формуле:

r = √R² — m²,

где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.

Определение. Полусфера (полушар) — это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.

Касательная, касательная плоскость к сфере и их свойства

Определение.Касательная к сфере — это прямая, которая касается сферы только в одной точке.

Определение.Касательная плоскость к сфере — это плоскость, которая соприкасается со сферой только в одной точке.

Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения

Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.

Определение. Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента. Формула. Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:

S = 2πRh

Формула. Объём сегмента сферы с высотой h через радиус сферы R: Определение. Срез шара — это часть шара, которая образуется в результате его сечения двумя параллельными плоскостями и находится между ними. Определение. Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r. Формула. Площадь поверхности сектора S с высотой O₁H (h) через радиус шара OH (R):

S = πR(2h + √2hR — h²)

Формула. Объём сектора V с высотой O₁H (h) через радиус шара OH (R):

Определение. Касательными сферами (шарами) называются любые две сферы (шара), которые имеют одну общую точку соприкосновения. Если расстояние между центрами больше суммы радиусов, то фигуры не касаются и не пересекаются.

Определение. Концентрическими сферами называются любые две сферы, которые имеют общий центр и радиусы различной длины.

Сектор круга и сегмент

Ломтики

Есть два основных «кусочка» круга:

• Кусочек «пиццы» называется Сектор .
• И сегмент , который отсечен от круга «хордой» (линия между двумя точками на окружности).

Попробуйте!

Общие сектора

Квадрант и Полукруг — это два особых типа сектора:

Полукруг — это
полукруг .

Четверть круга — это
, а Квадрант .

Площадь сектора

Вы можете рассчитать площадь сектора, сравнив его угол с углом полного круга.

Примечание: мы используем радианы для углов.

Это рассуждение:

Круг имеет угол 2π и площадь: πr ²

Сектор имеет угол θ вместо 2π, поэтому его площадь составляет: θ 2π × πr ²

Что можно упростить до: θ 2 × r ²

Площадь сектора = θ 2 × r ² (когда θ в радианах)

Площадь сектора = θ × π 360 × r ² (когда θ в градусах)

Площадь сегмента

Площадь сегмента — это площадь сектора за вычетом треугольника (здесь показан голубым).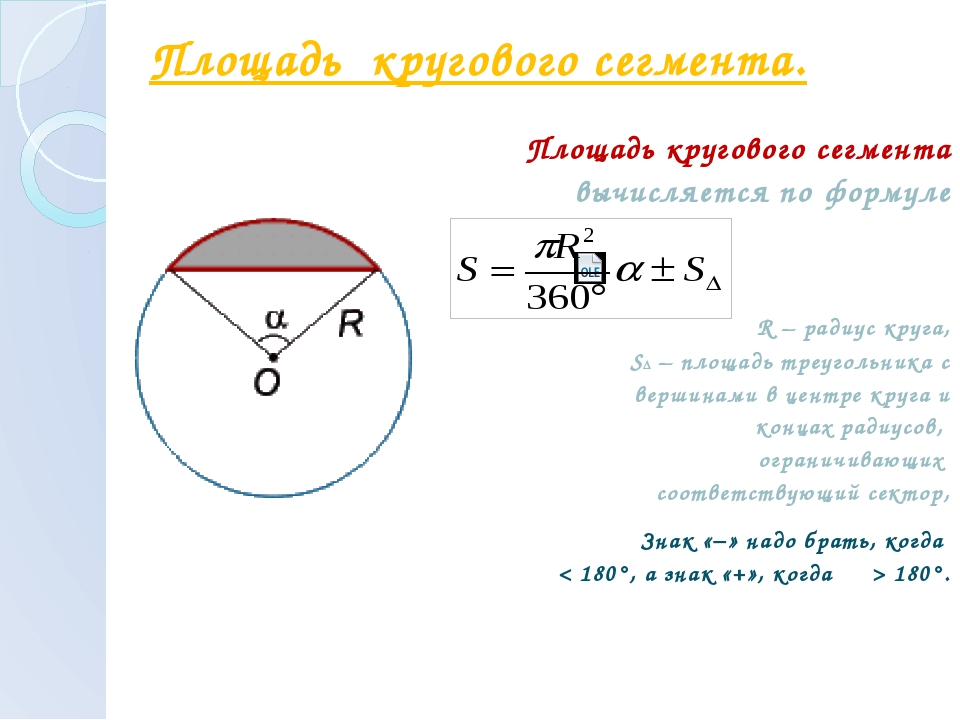

Есть длинная причина, но результатом является небольшая модификация формулы Сектора:

Площадь сегмента = θ — грех (θ) 2 × r ² (когда θ в радианах)

Площадь сегмента = ( θ × π 360 — sin (θ) 2 ) × r ² (когда θ в градусах)

Длина дуги

Длина дуги (сектора или сегмента ) составляет:

L = θ × r (когда θ в радианах)

L = θ × π 180 × r (когда θ в градусах)

Круг, диск, сегмент, сектор.Формулы, характеристики и свойства круга

Определение. Окружность — это совокупность всех точек на плоскости, которые равноудалены от данной точки О , называемой центром окружности .

Определение. Единичная окружность — это окружность, радиус которой равен единице.

Определение. Диск является частью плоскости, ограниченной окружностью.

Определение. Радиус окружности R — это расстояние от центра окружности О до любой точки окружности.

Определение. Диаметр окружности D — это отрезок, соединяющий две точки на окружности и проходящий через его центр.

Свойства круга

1. Диаметр круга равен двум радиусам.

D = 2r

2. Кратчайшее расстояние от центрального круга до секущей (хорды) всегда меньше радиуса.

3. Три точки, расположенные не на прямой, могут удерживать только один круг.

4. Среди всех замкнутых кривых равной длины круг имеет наибольшую площадь.

5. Если два круга соприкасаются в одной точке, эта точка размещается на линии, проходящей через центры кругов.

Площадь и длина окружности

Длина окружности

1. Формула длины окружности через диаметр:

С = πD

2. Формула длины окружности через радиус:

С = 2πr

Формула площади круга

1. Формула площади круга через радиус:

А = πr ²

2.Формула площади круга через диаметр:

А = πD ² 4

Уравнение окружности

1. Уравнение окружности с радиусом r и центром в начале декартовой координаты:

r ² = x ² + y ²

2. Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:

r ² = (x — a) ² + (y — b) ²

3. Параметрические уравнения окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:

{	x = a + r cos t
	y = b + r sin t

Касательная окружности и ее свойства

Определение. Касательная — это копланарная прямая линия, которая касается окружности в одной точке.

Касательные свойства

1. Касательная всегда перпендикулярна радиусу окружности, нарисованной в точке контакта.

2. Кратчайшее расстояние от центра окружности до касательной — это радиус окружности.

3. Если две касательные от точек касания B и C на одной и той же окружности не параллельны, они пересекаются в точке A, а точка соприкосновения между сегментом и точкой пересечения касательной является одним и тем же сегментом на другой касательной:

AB = AC

Кроме того, если вы проведете линию через центр O и точку пересечения A этих касательных, углы между этой линией и касательными будут равны:

∠ОAС = ∠OAB

Секущая круга и ее свойства

Определение. Секущая окружности — прямая линия, соединяющая две точки окружности.

Свойства секущей окружности

1. Если точка за пределами окружности (Q) имеет две секущие, пересекающие окружность в двух точках A и B для первой секущей и C и D для другой секущей, произведения двух пересекающихся сегментов равны:

AQ ∙ BQ = CQ ∙ DQ

2. Если точка выходит из секущей Q окружности, пересекая окружность в двух точках A и B и касательную точку контакта C, то произведение сегментирует секущую длину, равную квадрату касательной:

AQ ∙ BQ = CQ ²

Хорда круга и ее свойства

Определение. Хорда окружности — отрезок, соединяющий две точки окружности. Хорда — это отрезок касательной.

Длина пояса

1. Формула длины хорды через радиус и центральный угол:

AB = 2r sin α2

2. Формула длины хорды через радиус и вписанный угол:

AB = 2r sin α

Свойства аккорда

1. Две равные хорды стягивают две одинаковые дуги:

если аккорды AB = CD, то

дуги ◡ AB = ◡ CD

2.Если хорды параллельны, дуги между ними будут одинаковыми:

если аккорды AB ∣∣ CD, то

◡ нашей эры = ◡ BC

3. Если радиус окружности перпендикулярен хорде, он делит хорду пополам в точке пересечения:

, если OD ┴ AB, то

AC =

BC 4. Если две хорды AB и DE пересекаются в точке Q, то произведенные отрезки, образованные на пересечении, одна хорда является произведением разных хордовых отрезков:

AQ ∙ BQ = DQ ∙ QC

5. Хорды ​​одинаковой длины равноудалены от центра окружности.

если аккорды AB = CD, то

ВКЛ = ОК

6. Чем больше хорда, тем ближе она к центру.

если CD> AB, то

ВКЛ <ОК

Центральный угол и вписанный угол окружности и его свойства

Определение. Центральный угол окружности — это угол, вершина которого является центром окружности.

Определение. Вписанный угол — это угол внутри круга, вершина которого лежит на окружности.

Угловые свойства

1. Все вписанные углы, основанные на одной дуге, равны (один конец хорды). 2. Вписанный угол будет прямым (90 °), если он основан на диаметре круга. 3. Любой вписанный угол всегда равен половине центрального угла, основанного на той же дуге.

β = α2

4. Если два вписанных угла основаны на хорде и расположены по обе стороны от нее, сумма углов составляет 180 °.

α + β = 180 °

Определение. Дуга окружности (◡) — часть окружности, соединяющая две точки на окружности.

Определение. Угол выступа дуги — это угол между двумя радиусами, которые ограничивают эту дугу. Угловая дуга выступа всегда равна центральному углу между радиусами, ограничивающим конечные точки этой дуги.

Формула длины дуги через центральные углы (в градусах) и радиус:

l = πr180 ° ∙ α

Определение. Полукруг — это дуга, концы которой соединены диаметром окружности.

Определение. Semidisc (◓) — это часть диска, ограниченная полукругом и диаметром.

Определение. Сектор (◔) является частью диска, который ограничен двумя радиусами и дугой между ними.

Формула. Формула площади сектора через радиус и центральные углы (в градусах)

A = πr ² 360 ° ∙ α

Определение. Сегмент является частью диска, который ограничен дугой и хордой, соединяющей концы этой дуги.

Определение. Концентрическая окружность — окружность разных радиусов с общим центром.

Определение. Кольцо — это часть плоскости, ограниченная двумя концентрическими окружностями.

Теоремы о круге — Математика GCSE Revision

Теоремы

В этом разделе объясняется теорема окружности, включая касательные, сектора, углы и доказательства.

В видео ниже показаны правила, которые нужно помнить при построении теорем о кругах.

Равнобедренный треугольник

Два радиуса и хорда образуют равнобедренный треугольник.

Биссечение перпендикулярной хорды

Перпендикуляр от центра окружности к хорде всегда будет делить хорду пополам (разделять его на две равные длины).

Углы, расположенные на одной дуге

Углы, образованные из двух точек на окружности, равны другим углам в той же дуге, образованным из этих двух точек.

Угол по полукругу

Углы, образованные проведением линий от концов диаметра круга к его окружности, образуют прямой угол. Итак, c — это прямой угол .

Проба

Мы можем разделить треугольник пополам, проведя линию от центра круга до точки на окружности, которой соприкасается наш треугольник.

Мы знаем, что каждая из линий, являющихся радиусом круга (зеленые линии), имеет одинаковую длину. Следовательно, каждый из двух треугольников равнобедренный и имеет пару равных углов.

Но все эти углы вместе должны составлять 180 °, так как они являются углами исходного большого треугольника.

Следовательно, x + y + x + y = 180, другими словами 2 (x + y) = 180.
и поэтому x + y = 90. Но x + y — это размер угла, который мы хотели найти.

Касательные

Касательная к окружности — это прямая линия, которая касается окружности только в одной точке (поэтому она не пересекает окружность, а только касается ее).

Касательная к окружности образует прямой угол с радиусом окружности в точке контакта касательной.

Кроме того, если две касательные нарисованы на окружности и они пересекаются, длины этих двух касательных (от точки, где они касаются круга, до точки, где они пересекаются) будут одинаковыми.

Угол в центре

Угол, образованный в центре круга линиями, начинающимися из двух точек на окружности окружности, в два раза больше угла, образованного на окружности окружности линиями, берущими начало в тех же точках. то есть a = 2b .

Проба

Возможно, вам придется доказать этот факт:

OA = OX, поскольку оба они равны радиусу круга.Следовательно, треугольник AOX равнобедренный, поэтому ∠OXA = a
. Аналогично, OXB = b

.

Поскольку в сумме углы в треугольнике равны 180, мы знаем, что ∠XOA = 180 — 2a
Точно так же ∠BOX = 180 — 2b
Поскольку углы вокруг точки в сумме составляют 360, мы имеем ∠AOB = 360 — ∠XOA — ∠BOX
= 360 — (180 — 2a) — (180 — 2b)
= 2a + 2b = 2 (a + b) = 2 ∠AXB

Теорема об альтернативном сегменте

На этой диаграмме показана теорема об альтернативном сегменте . Короче говоря, красные углы равны друг другу, а зеленые углы равны друг другу.

Проба

Возможно, вам придется доказать теорему об альтернативном отрезке:

Мы используем факты о связанных углах

Касательная составляет угол 90 градусов с радиусом окружности, поэтому мы знаем, что ∠OAC + x = 90.
Угол в полукруге равен 90, поэтому ∠BCA = 90.
Углы в треугольнике складываем до 180, поэтому ∠BCA + ∠OAC + y = 180
Следовательно, 90 + ∠OAC + y = 180 и, следовательно, ∠OAC + y = 90
Но OAC + x = 90, поэтому ∠OAC + x = ∠OAC + y
Следовательно, x = y

Циклический четырехугольник

Циклический четырехугольник — это четырехсторонняя фигура в окружности, каждая вершина (угол) четырехугольника которой касается окружности окружности.Противоположные углы такого четырехугольника в сумме составляют 180 градусов.

Площадь сектора и длина дуги

Если радиус окружности равен r,
Площадь сектора = πr ² × A / 360
Длина дуги = 2πr × A / 360

Другими словами, площадь сектора = площадь круга × A / 360
длина дуги = длина окружности × A / 360

Для получения дополнительной информации об определениях кругов щелкните здесь

.