Путь и перемещение, теория и онлайн калькуляторы
Путь и перемещение, теория и онлайн калькуляторыПри своем движении материальная точка описывает некоторую линию, которую называют ее траекторией движения. Траектория может быть прямой линией, а может представлять собой кривую.
Путь
Определение
Путь — длина участка траектории, который прошла материальная точка за рассматриваемый отрезок времени. Путь — это скалярная величина.
При прямолинейном движении в одном направлении пройденный путь ($\Delta s$) равен модулю изменения координаты тела. Так, если тело двигалось по оси X, то путь можно найти как:
\[\Delta s=\left|x_2-x_1\right|\left(1\right),\]
где $x_1$ — координата начального положения тела; $x_2$ — конечная координата тела.
Его можно вычислить, если известен модуль скорости ($v=v_x$):
\[\Delta s=vt\ \left(2\right),\]
где $t$ — время движения тела.
Графиком, который отображает зависимость пути от времени при равномерном прямолинейном движении, является прямая (рис.1). С увеличением величины скорости увеличивается угол наклона прямой относительно оси времени.
Если по графику $\Delta s(t)$ необходимо найти путь, который проделало тело за время $t_1$, то из точки $t_1$ на оси времени проводят перпендикуляр до пересечения с графиком $\Delta s(t)$. Затем из точки пересечения восстанавливают перпендикуляр к оси $\Delta s$. На пересечении оси и перпендикуляра получают точку ${\Delta s}_1$, которая соответствует пройденному пути за время от $t=0\ c$ до $t_1$.
Путь не бывает меньше нуля и не может уменьшаться при движении тела.
Перемещение
Определение
Перемещением называют вектор, который проводят из начального положения движущейся материальной точки в ее конечное положение:
\[\Delta \overline{r}=\overline{r\ }\left(t+\Delta t\right)-\overline{r\ }\left(t\right)\left(3\right). \]
\]
Вектор перемещения численно равен расстоянию между конечной и начальной точками и направлен от начальной точки к конечной.
Приращение радиус-вектора материальной точки — это перемещение ($\Delta \overline{r}$).
В декартовой системе координат радиус-вектор точки представляют в виде:
\[\overline{r\ }\left(t\right)=x\left(t\right)\overline{i}+y\left(t\right)\overline{j}+z\left(t\right)\overline{k}\left(4\right),\]
где $\overline{i}$, $\overline{j}$,$\ \overline{k}$ — единичные орты осей X,Y,Z. Тогда $\Delta \overline{r}$ равен:
\[\Delta \overline{r}=\left[x\left(t+\Delta t\right)-x\left(t\right)\right]\overline{i}+\left[y\left(t+?t\right)-y\left(t\right)\right]\overline{j}+\left[z\left(t+?t\right)-z\left(t\right)\right]\overline{k}\left(5\right).\]
При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и длина вектора перемещения равна пройденному точкой пути:
\[\left|\Delta \overline{r}\right|=\Delta s\ \left(6\right).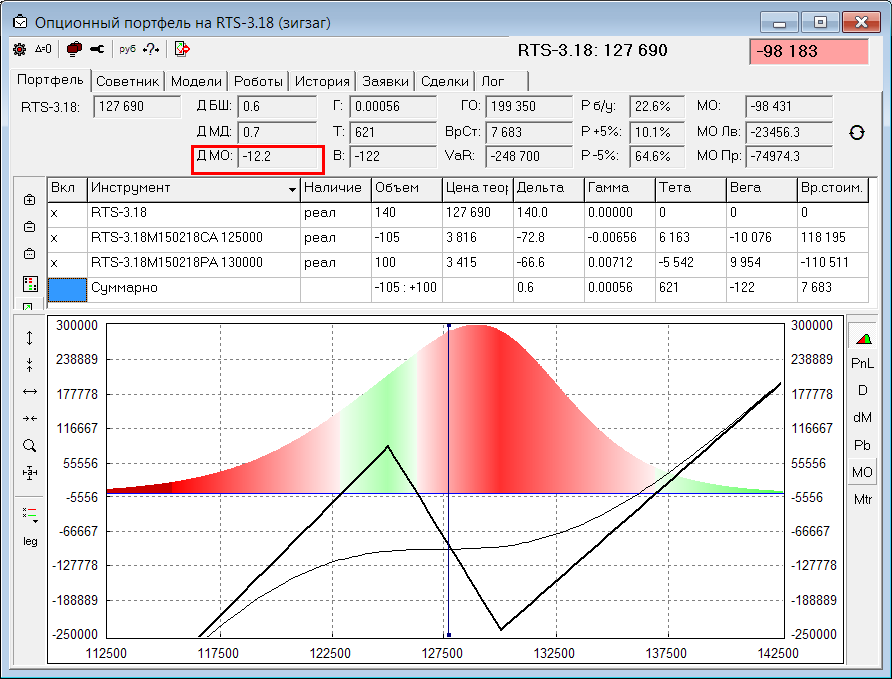
Длину вектора перемещения (как и любого вектора) можно обозначать как $\left|\Delta \overline{r}\right|$ или просто $\Delta r$ (без указания стрелки).
Если тело совершает несколько перемещений, то их можно складывать по правилам сложения векторов:
\[\Delta \overline{r}=\Delta {\overline{r}}_1+\Delta {\overline{r}}_2+\dots \left(7\right).\]
Если направление движения тела изменяется, то модуль вектора перемещения не равен пройденному телом пути.
Примеры задач на путь и перемещение
Пример 1
Задание: Мяч бросили вертикально вверх от поверхности Земли. Он долетел до высоты 20 м. и упал на Землю. Чему равен путь, который прошел мяч, каков модуль перемещения?
Решение: Сделаем рисунок.
В нашей задаче мяч движется прямолинейно сначала вверх, затем вниз. Так как путь — длина траектории, то получается, что мяч дважды прошел расстояние h, следовательно:
\[\Delta s=2h. \]
\]
Перемещение — направленный отрезок, соединяющий начальную точку и конечную при движении тела, но тело начало движение из той же точки, в которую вернулось, следовательно, перемещение мяча равно нулю:
\[\Delta r=0.\]
Ответ: $\ Путь\ \Delta s=2h$. Перемещение $\Delta r=0$
Пример 2
Задание: В начальный момент времени тело находилось в точке с координатами $(x_0=3;;\ y_0=1)$(см). Через некоторый промежуток времени оно переместилось в точку координаты которой ($x=2;;y=4$) (см). Каковы проекции вектора перемещения на оси X и Y?
Решение: Сделаем рисунок.
Радиус — вектор начальной точки запишем как:
\[{\overline{r\ }}_0\left(t\right)=x_0\left(t\right)\overline{i}+y_0\left(t\right)\overline{j}=3\overline{i}+1\overline{j}\left(2.1\right).\]
Радиус — вектор конечной точки имеет вид:
\[\overline{r}\left(t\right)=x\left(t\right)\overline{i}+y\left(t\right)\overline{j}=2\overline{i}+4\overline{j}\left(2. 2\right).\]
2\right).\]
Вектор перемещения представим как:
\[\Delta \overline{r}=\left[x\left(t\right)-x_0\left(t\right)\right]\overline{i}+\left[у\left(t\right)-у_0\left(t\right)\right]\overline{j}=\left[2-3\right]+\left[1-4\right]\overline{j}=-1\overline{i}+3\overline{j}(2.3).\]
Из формулы видим, что:
\[\Delta r_x=-1;;\Delta r_y=3.\ \]
Ответ: $\Delta r_x=-1;;\Delta r_y=3\ $
Читать дальше: равнодействующая всех сил.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Кинематика | Формулы по физике
Путь, время, скорость
Найти
Известно, что:
Svt =
Вычислить ‘S’Равномерное движение
Найти
Известно, что:
xx_0vt =
Равномерно ускоренное движение: ускорение
Найти
Известно, что:
avv0t =
Вычислить ‘a’Равномерно ускоренное движение: скорость
Найти
Известно, что:
vv0at =
Вычислить ‘v’Равномерно ускоренное движение: путь
Найти
Известно, что:
svta =
Вычислить ‘s’Равномерно ускоренное движение: координата
НайтиИзвестно, что:
xx0vta =
Вычислить ‘x’Высота тела, брошенного вертикально вверх (вниз)
Найти
Известно, что:
hh0v0tg =
Вычислить ‘h’Скорость тела, брошенного вертикально вверх (вниз)
Найти
Известно, что:
vv0gt =
Вычислить ‘v’Скорость, ускорение, время
Найти
Известно, что:
vat =
Вычислить ‘v’Скорость свободно падающего тела
Найти
Известно, что:
vgt =
Вычислить ‘v’Центростремительное ускорение
Найти
Известно, что:
avR =
Вычислить ‘a’Угловая скорость
Найти
Известно, что:
ωφt =
Вычислить ‘ω’Равномерное круговое движение
Найти
Известно, что:
lRφ =
Вычислить ‘l’Равномерное круговое движение: линейная скорость
Найти
Известно, что:
vRω =
Вычислить ‘v’Период вращения
Найти
Известно, что:
TtN =
Вычислить ‘T’Период вращения
Найти
Известно, что:
Период вращения
Найти
Известно, что:
Tπω =
Вычислить ‘T’Центростремительное ускорение
Найти
Известно, что:
aπRT =
Вычислить ‘a’Центростремительное ускорение
Найти
Известно, что:
aπRn =
Вычислить ‘a’Частота вращения
Найти
Известно, что:
nT =
Вычислить ‘n’Центростремительное ускорение
Найти
Известно, что:
aωR =
Вычислить ‘a’Дальность броска тела, брошенного под углом к горизонту
Найти
Известно, что:
xv0tα =
Вычислить ‘x’Высота подъема тела, брошенного под углом к горизонту
Найти
Известно, что:
yv0tαg =
Вычислить ‘y’Вертикальная скорость тела, брошенного под углом к горизонту
Найти
Известно, что:
v_yv0αgt =
Вычислить ‘v_y’Максимальная высота подъема тела, брошенного под углом к горизонту
Найти
Известно, что:
h_максv0αg =
Вычислить ‘h_макс’Общее время движения тела, брошенного под углом к горизонту
Найти
Известно, что:
tv0αg =
Вычислить ‘t’Максимальная дальность броска тела, брошенного под углом к горизонту
Найти
Известно, что:
s_максv0g =
Вычислить ‘s_макс’Дальность броска тела, брошенного горизонтально
Найти
Известно, что:
xx0vt =
Вычислить ‘x’Высота подъема тела, брошенного горизонтально
Найти
Известно, что:
yy0gt =
Вычислить ‘y’Общее время движения тела, брошенного горизонтально
Найти
Известно, что:
t_максhg =
Вычислить ‘t_макс’§6.
 Примеры движения тела. Методы решения задач. — ЗФТШ, МФТИ
Примеры движения тела. Методы решения задач. — ЗФТШ, МФТИРассмотрим некоторые характерные примеры движения тела, знание которых будет полезно при дальнейшем изучении физики.
1.Равномерное прямолинейное движение тела.
При равномерном прямолинейном движении тело совершает равные перемещения `Delta vecr` за одинаковые промежутки времени `Delta t`. Иными словами, скорость `vec v` тела не зависит от времени и остаётся постоянной в процессе движения:
При этом зависимость `vec r(t)` имеет вид:
где `vec r_0` — радиус-вектор тела в начальный момент времени $$ t=0$$ . В этой связи вспомним замечание о начальных условиях, сделанное в §4. Вектор $$ {\overrightarrow{r}}_{0}$$ здесь является тем начальным условием, которое позволяет однозначно определить радиус-вектор $$ \overrightarrow{r}$$ тела в любой момент времени в процессе движения.
Векторное уравнение (7) равносильно системе двух скалярных уравнений, выражающих зависимость от времени $$ t $$ координат $$ x$$ и $$ y$$ движущегося тела:
где $$ {x}_{0}$$ и $$ {y}_{0}$$ — начальные координаты тела в момент времени $$ t=0$$, а $$ {v}_{x}$$ и $$ {v}_{y}$$ -проекции вектора скорости `vecv` на координатные оси $$ Ox$$ и $$ Oy$$ соответственно.
Траектория равномерного прямолинейного движения тела графически представляет собой отрезок прямой линии (рис. 9), тангенс угла наклона которой к оси абсцисс равен отношению проекций скорости на оси координат: $$ \mathrm{tg}\alpha ={v}_{y}/{v}_{x}$$. Аналитическое уравнение траектории, т. е. зависимость $$ y\left(x\right)$$, легко получить, исключив параметр $$ t$$ из системы уравнений (8):
2. Неравномерное движение тела.
Для неравномерного движения характерно то, что с течением времени изменяется скорость движущегося тела, а в общем случае и его ускорение. В качестве примера может служить движение, при котором тело проходит различные участки своего пути с разной скоростью. Такое движение принято характеризовать, прежде всего, средней путевой скоростью. Причём прилагательное «путевая» в условиях задач часто опускается.
Другим характерным примером неравномерного движения служит так называемое равнопеременное движение, которое целесообразно рассмотреть подробно, не выходя при этом за рамки школьной программы.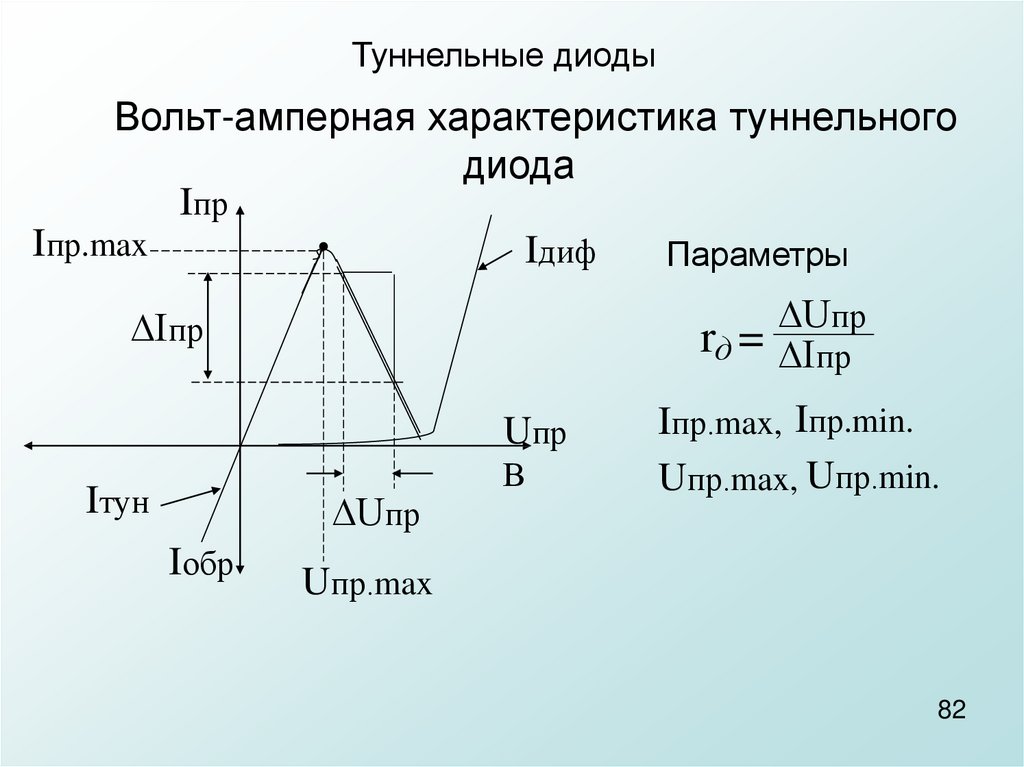
3. Равнопеременное движение.
Равнопеременным называется такое неравномерное движение, при котором скорость `vec v` за любые равные промежутки времени `Delta t` изменяется на одинаковую величину `Deltavecv`. В этом случае ускорение `veca` тела не зависит от времени и остаётся постоянным в процессе движения:
(при этом `vec v != «const»`, и траектория движения не обязательно прямолинейная).
При равнопеременном движении скорость $$ \overrightarrow{v}$$ тела изменяется с течением времени по закону
где `vecv_0` — скорость тела в начальный момент времени `t=0`.
В свою очередь, зависимость `vecr(t)` имеет вид:
где `vecr_0` — начальный радиус-вектор тела при `t=0`. Вновь заметим, что величины `vecv_0` и `vecr_0` представляют собой начальные условия, позволяющие в любой момент времени однозначно определить векторы `vecv` и `vecr`.
При координатном способе описания равнопеременного движения векторным уравнениям (11) и (12), равносильны следующие системы уравнений для проекций скорости и радиус-вектора тела на оси выбранной системы отсчёта. 2)/(2a_x)`.
2)/(2a_x)`.
Удобство этой формулы заключается в том, что она не содержит времени $$ t$$ в явном виде. Вместе с тем надо помнить, что формула получена в предположении о неизменности направления движения тела.
Одним из наиболее наглядных примеров равнопеременного движения является движение тела в поле тяжести Земли, которое мы имеем возможность наблюдать повседневно. Для решения задач в этом случае надо заменить в приведённых выше формулах вектор $$ \overrightarrow{a}$$ на ускорение свободного падения $$ \overrightarrow{g}$$, сообщаемое силой гравитационного притяжения всякому телу, движущемуся в поле тяжести Земли. Рассмотрим три конкретных случая такого движения.
Движение тела, брошенного вертикально.
Тело бросили с поверхности земли, сообщив ему начальную скорость $$ {\overrightarrow{v}}_{0}$$ направленную вертикально вверх. Пренебрегая сопротивлением воздуха, определите время $$ \tau $$ полёта тела до момента падения на землю; скорость тела в момент падения; максимальную высоту $$ H$$ подъёма тела над землёй; время $$ {\tau }_{1}$$ подъёма тела на максимальную высоту; путь `S`, пройденный телом за время полёта и перемещение тела.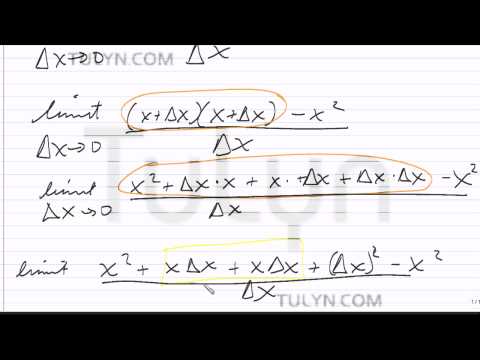 {2}+\mathrm{tg}\alpha x$$.
{2}+\mathrm{tg}\alpha x$$.
График траектории тела представляетсобой участок параболы, ветви которой направлены вниз.
Все главные формулы по физике — Физика — Теория, тесты, формулы и задачи
Оглавление:
- Кинематика
- Динамика
- Статика
- Гидростатика
- Импульс
- Работа, мощность, энергия
- Молекулярная физика
- Термодинамика
- Электростатика
- Электрический ток
- Магнетизм
- Колебания
- Оптика
- Атомная и ядерная физика
- Основы специальной теории относительности (СТО)
- Равномерное движение по окружности
- Расширенная PDF версия документа «Все главные формулы по школьной физике»
Кинематика
К оглавлению…
Путь при равномерном движении:
Перемещение S (расстояние по прямой между начальной и конечной точкой движения) обычно находится из геометрических соображений. Координата при равномерном прямолинейном движении изменяется по закону (аналогичные уравнения получаются для остальных координатных осей):
Координата при равномерном прямолинейном движении изменяется по закону (аналогичные уравнения получаются для остальных координатных осей):
Средняя скорость пути:
Средняя скорость перемещения:
Определение ускорения при равноускоренном движении:
Выразив из формулы выше конечную скорость, получаем более распространённый вид предыдущей формулы, которая теперь выражает зависимость скорости от времени при равноускоренном движении:
Средняя скорость при равноускоренном движении:
Перемещение при равноускоренном прямолинейном движении может быть рассчитано по нескольким формулам:
Координата при равноускоренном движении изменяется по закону:
Проекция скорости при равноускоренном движении изменяется по такому закону:
Скорость, с которой упадет тело падающее с высоты h без начальной скорости:
Время падения тела с высоты h без начальной скорости:
Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v0, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):
Формула для тормозного пути тела:
Время падения тела при горизонтальном броске с высоты H может быть найдено по формуле:
Дальность полета тела при горизонтальном броске с высоты H:
Полная скорость в произвольный момент времени при горизонтальном броске, и угол наклона скорости к горизонту:
Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
Время подъема до максимальной высоты при броске под углом к горизонту:
Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т. е. тело бросали, например, с земли на землю):
е. тело бросали, например, с земли на землю):
Определение периода вращения при равномерном движении по окружности:
Определение частоты вращения при равномерном движении по окружности:
Связь периода и частоты:
Линейная скорость при равномерном движении по окружности может быть найдена по формулам:
Угловая скорость вращения при равномерном движении по окружности:
Связь линейной и скорости и угловой скорости выражается формулой:
Связь угла поворота и пути при равномерном движении по окружности радиусом R (фактически, это просто формула для длины дуги из геометрии):
Центростремительное ускорение находится по одной из формул:
Динамика
К оглавлению…
Второй закон Ньютона:
Здесь: F — равнодействующая сила, которая равна сумме всех сил действующих на тело:
Второй закон Ньютона в проекциях на оси (именно такая форма записи чаще всего и применяется на практике):
Третий закон Ньютона (сила действия равна силе противодействия):
Сила упругости:
Общий коэффициент жесткости параллельно соединённых пружин:
Общий коэффициент жесткости последовательно соединённых пружин:
Сила трения скольжения (или максимальное значение силы трения покоя):
Закон всемирного тяготения:
Если рассмотреть тело на поверхности планеты и ввести следующее обозначение:
Где: g — ускорение свободного падения на поверхности данной планеты, то получим следующую формулу для силы тяжести:
Ускорение свободного падения на некоторой высоте от поверхности планеты выражается формулой:
Скорость спутника на круговой орбите:
Первая космическая скорость:
Закон Кеплера для периодов обращения двух тел вращающихся вокруг одного притягивающего центра:
Статика
К оглавлению. ..
..
Момент силы определяется с помощью следующей формулы:
Условие при котором тело не будет вращаться:
Координата центра тяжести системы тел (аналогичные уравнения для остальных осей):
Гидростатика
К оглавлению…
Определение давления задаётся следующей формулой:
Давление, которое создает столб жидкости находится по формуле:
Но часто нужно учитывать еще и атмосферное давление, тогда формула для общего давления на некоторой глубине h в жидкости приобретает вид:
Идеальный гидравлический пресс:
Любой гидравлический пресс:
КПД для неидеального гидравлического пресса:
Сила Архимеда (выталкивающая сила, V — объем погруженной части тела):
Импульс
К оглавлению…
Импульс тела находится по следующей формуле:
Изменение импульса тела или системы тел (обратите внимание, что разность конечного и начального импульсов векторная):
Общий импульс системы тел (важно то, что сумма векторная):
Второй закон Ньютона в импульсной форме может быть записан в виде следующей формулы:
Закон сохранения импульса.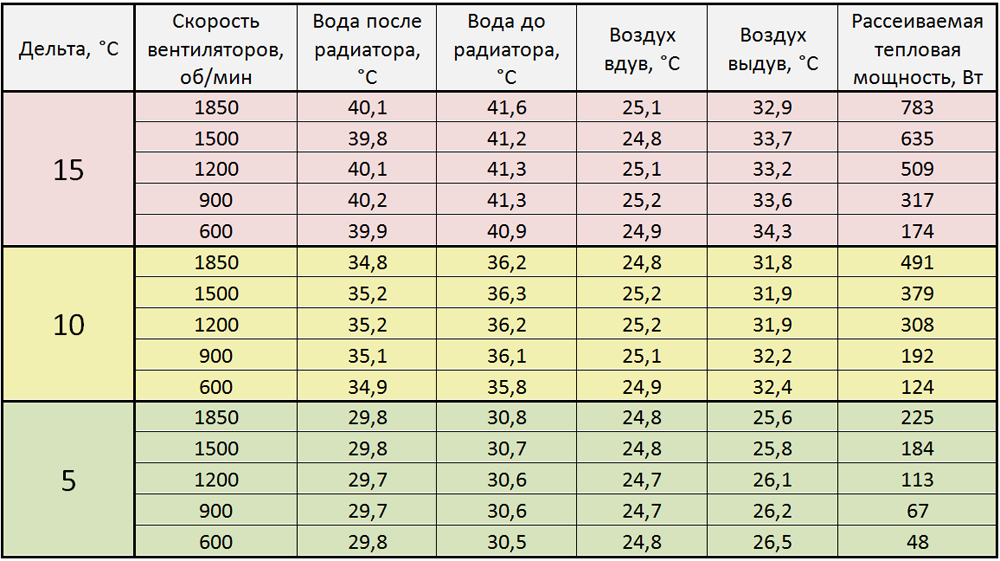 Как следует из предыдущей формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:
Как следует из предыдущей формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:
Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:
Работа, мощность, энергия
К оглавлению…
Механическая работа рассчитывается по следующей формуле:
Самая общая формула для мощности (если мощность переменная, то по следующей формуле рассчитывается средняя мощность):
Мгновенная механическая мощность:
Коэффициент полезного действия (КПД) может быть рассчитан и через мощности и через работы:
Формула для кинетической энергии:
Потенциальная энергия тела поднятого на высоту:
Потенциальная энергия растянутой (или сжатой) пружины:
Полная механическая энергия:
Связь полной механической энергии тела или системы тел и работы внешних сил:
Закон сохранения механической энергии (далее – ЗСЭ). Как следует из предыдущей формулы, если внешние силы не совершают работы над телом (или системой тел), то его (их) общая полная механическая энергия остается постоянной, при этом энергия может перетекать из одного вида в другой (из кинетической в потенциальную или наоборот):
Как следует из предыдущей формулы, если внешние силы не совершают работы над телом (или системой тел), то его (их) общая полная механическая энергия остается постоянной, при этом энергия может перетекать из одного вида в другой (из кинетической в потенциальную или наоборот):
Молекулярная физика
К оглавлению…
Химическое количество вещества находится по одной из формул:
Масса одной молекулы вещества может быть найдена по следующей формуле:
Связь массы, плотности и объёма:
Основное уравнение молекулярно-кинетической теории (МКТ) идеального газа:
Определение концентрации задаётся следующей формулой:
Для средней квадратичной скорости молекул имеется две формулы:
Средняя кинетическая энергия поступательного движения одной молекулы:
Постоянная Больцмана, постоянная Авогадро и универсальная газовая постоянная связаны следующим образом:
Следствия из основного уравнения МКТ:
Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева):
Газовые законы. Закон Бойля-Мариотта:
Закон Бойля-Мариотта:
Закон Гей-Люссака:
Закон Шарля:
Универсальный газовый закон (Клапейрона):
Давление смеси газов (закон Дальтона):
Тепловое расширение тел. Тепловое расширение газов описывается законом Гей-Люссака. Тепловое расширение жидкостей подчиняется следующему закону:
Для расширения твердых тел применяются три формулы, описывающие изменение линейных размеров, площади и объема тела:
Термодинамика
К оглавлению…
Количество теплоты (энергии) необходимое для нагревания некоторого тела (или количество теплоты выделяющееся при остывании тела) рассчитывается по формуле:
Теплоемкость (С — большое) тела может быть рассчитана через удельную теплоёмкость (c — маленькое) вещества и массу тела по следующей формуле:
Тогда формула для количества теплоты необходимой для нагревания тела, либо выделившейся при остывании тела может быть переписана следующим образом:
Фазовые превращения. При парообразовании поглощается, а при конденсации выделяется количество теплоты равное:
При парообразовании поглощается, а при конденсации выделяется количество теплоты равное:
При плавлении поглощается, а при кристаллизации выделяется количество теплоты равное:
При сгорании топлива выделяется количество теплоты равное:
Уравнение теплового баланса (ЗСЭ). Для замкнутой системы тел выполняется следующее (сумма отданных теплот равна сумме полученных):
Если все теплоты записывать с учетом знака, где «+» соответствует получению энергии телом, а «–» выделению, то данное уравнение можно записать в виде:
Работа идеального газа:
Если же давление газа меняется, то работу газа считают, как площадь фигуры под графиком в p–V координатах. Внутренняя энергия идеального одноатомного газа:
Изменение внутренней энергии рассчитывается по формуле:
Первый закон (первое начало) термодинамики (ЗСЭ):
Для различных изопроцессов можно выписать формулы по которым могут быть рассчитаны полученная теплота Q, изменение внутренней энергии ΔU и работа газа A. Изохорный процесс (V = const):
Изохорный процесс (V = const):
Изобарный процесс (p = const):
Изотермический процесс (T = const):
Адиабатный процесс (Q = 0):
КПД тепловой машины может быть рассчитан по формуле:
Где: Q1 – количество теплоты полученное рабочим телом за один цикл от нагревателя, Q2 – количество теплоты переданное рабочим телом за один цикл холодильнику. Работа совершенная тепловой машиной за один цикл:
Наибольший КПД при заданных температурах нагревателя T1 и холодильника T2, достигается если тепловая машина работает по циклу Карно. Этот КПД цикла Карно равен:
Абсолютная влажность рассчитывается как плотность водяных паров (из уравнения Клапейрона-Менделеева выражается отношение массы к объему и получается следующая формула):
Относительная влажность воздуха может быть рассчитана по следующим формулам:
Потенциальная энергия поверхности жидкости площадью S:
Сила поверхностного натяжения, действующая на участок границы жидкости длиной L:
Высота столба жидкости в капилляре:
При полном смачивании θ = 0°, cos θ = 1. В этом случае высота столба жидкости в капилляре станет равной:
В этом случае высота столба жидкости в капилляре станет равной:
При полном несмачивании θ = 180°, cos θ = –1 и, следовательно, h < 0. Уровень несмачивающей жидкости в капилляре опускается ниже уровня жидкости в сосуде, в которую опущен капилляр.
Электростатика
К оглавлению…
Электрический заряд может быть найден по формуле:
Линейная плотность заряда:
Поверхностная плотность заряда:
Объёмная плотность заряда:
Закон Кулона (сила электростатического взаимодействия двух электрических зарядов):
Где: k — некоторый постоянный электростатический коэффициент, который определяется следующим образом:
Напряжённость электрического поля находится по формуле (хотя чаще эту формулу используют для нахождения силы действующей на заряд в данном электрическом поле):
Принцип суперпозиции для электрических полей (результирующее электрическое поле равно векторной сумме электрических полей составляющих его):
Напряженность электрического поля, которую создает заряд Q на расстоянии r от своего центра:
Напряженность электрического поля, которую создает заряженная плоскость:
Потенциальная энергия взаимодействия двух электрических зарядов выражается формулой:
Электрическое напряжение это просто разность потенциалов, т. е. определение электрического напряжения может быть задано формулой:
е. определение электрического напряжения может быть задано формулой:
В однородном электрическом поле существует связь между напряженностью поля и напряжением:
Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов:
Работа электрического поля в общем случае может быть вычислена также и по одной из формул:
В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле:
Определение потенциала задаётся выражением:
Потенциал, который создает точечный заряд или заряженная сфера:
Принцип суперпозиции для электрического потенциала (результирующий потенциал равен скалярной сумме потенциалов полей составляющих итоговое поле):
Для диэлектрической проницаемости вещества верно следующее:
Определение электрической ёмкости задаётся формулой:
Ёмкость плоского конденсатора:
Заряд конденсатора:
Напряжённость электрического поля внутри плоского конденсатора:
Сила притяжения пластин плоского конденсатора:
Энергия конденсатора (вообще говоря, это энергия электрического поля внутри конденсатора):
Объёмная плотность энергии электрического поля:
Электрический ток
К оглавлению. ..
..
Сила тока может быть найдена с помощью формулы:
Плотность тока:
Сопротивление проводника:
Зависимость сопротивления проводника от температуры задаётся следующей формулой:
Закон Ома (выражает зависимость силы тока от электрического напряжения и сопротивления):
Закономерности последовательного соединения:
Закономерности параллельного соединения:
Электродвижущая сила источника тока (ЭДС) определяется с помощью следующей формулы:
Закон Ома для полной цепи:
Падение напряжения во внешней цепи при этом равно (его еще называют напряжением на клеммах источника):
Сила тока короткого замыкания:
Работа электрического тока (закон Джоуля-Ленца). Работа А электрического тока протекающего по проводнику обладающему сопротивлением преобразуется в теплоту Q выделяющуюся на проводнике:
Мощность электрического тока:
Энергобаланс замкнутой цепи
Полезная мощность или мощность, выделяемая во внешней цепи:
Максимально возможная полезная мощность источника достигается, если R = r и равна:
Если при подключении к одному и тому же источнику тока разных сопротивлений R1 и R2 на них выделяются равные мощности то внутреннее сопротивление этого источника тока может быть найдено по формуле:
Мощность потерь или мощность внутри источника тока:
Полная мощность, развиваемая источником тока:
КПД источника тока:
Электролиз
Масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q, прошедшему через электролит:
Величину k называют электрохимическим эквивалентом. Он может быть рассчитан по формуле:
Он может быть рассчитан по формуле:
Где: n – валентность вещества, NA – постоянная Авогадро, M – молярная масса вещества, е – элементарный заряд. Иногда также вводят следующее обозначение для постоянной Фарадея:
Магнетизм
К оглавлению…
Сила Ампера, действующая на проводник с током помещённый в однородное магнитное поле, рассчитывается по формуле:
Момент сил действующих на рамку с током:
Сила Лоренца, действующая на заряженную частицу движущуюся в однородном магнитном поле, рассчитывается по формуле:
Радиус траектории полета заряженной частицы в магнитном поле:
Модуль индукции B магнитного поля прямолинейного проводника с током I на расстоянии R от него выражается соотношением:
Индукция поля в центре витка с током радиусом R:
Внутри соленоида длиной l и с количеством витков N создается однородное магнитное поле с индукцией:
Магнитная проницаемость вещества выражается следующим образом:
Магнитным потоком Φ через площадь S контура называют величину заданную формулой:
ЭДС индукции рассчитывается по формуле:
При движении проводника длиной l в магнитном поле B со скоростью v также возникает ЭДС индукции (проводник движется в направлении перпендикулярном самому себе):
Максимальное значение ЭДС индукции в контуре состоящем из N витков, площадью S, вращающемся с угловой скоростью ω в магнитном поле с индукцией В:
Индуктивность катушки:
Где: n — концентрация витков на единицу длины катушки:
Связь индуктивности катушки, силы тока протекающего через неё и собственного магнитного потока пронизывающего её, задаётся формулой:
ЭДС самоиндукции возникающая в катушке:
Энергия катушки (вообще говоря, это энергия магнитного поля внутри катушки):
Объемная плотность энергии магнитного поля:
Колебания
К оглавлению. ..
..
Уравнение описывающее физические системы способные совершать гармонические колебания с циклической частотой ω0:
Решение предыдущего уравнения является уравнением движения для гармонических колебаний и имеет вид:
Период колебаний вычисляется по формуле:
Частота колебаний:
Циклическая частота колебаний:
Зависимость скорости от времени при гармонических механических колебаниях выражается следующей формулой:
Максимальное значение скорости при гармонических механических колебаниях:
Зависимость ускорения от времени при гармонических механических колебаниях:
Максимальное значение ускорения при механических гармонических колебаниях:
Циклическая частота колебаний математического маятника рассчитывается по формуле:
Период колебаний математического маятника:
Циклическая частота колебаний пружинного маятника:
Период колебаний пружинного маятника:
Максимальное значение кинетической энергии при механических гармонических колебаниях задаётся формулой:
Максимальное значение потенциальной энергии при механических гармонических колебаниях пружинного маятника:
Взаимосвязь энергетических характеристик механического колебательного процесса:
Энергетические характеристики и их взаимосвязь при колебаниях в электрическом контуре:
Период гармонических колебаний в электрическом колебательном контуре определяется по формуле:
Циклическая частота колебаний в электрическом колебательном контуре:
Зависимость заряда на конденсаторе от времени при колебаниях в электрическом контуре описывается законом:
Зависимость электрического тока протекающего через катушку индуктивности от времени при колебаниях в электрическом контуре:
Зависимость напряжения на конденсаторе от времени при колебаниях в электрическом контуре:
Максимальное значение силы тока при гармонических колебаниях в электрическом контуре может быть рассчитано по формуле:
Максимальное значение напряжения на конденсаторе при гармонических колебаниях в электрическом контуре:
Переменный ток характеризуется действующими значениями силы тока и напряжения, которые связаны с амплитудными значениями соответствующих величин следующим образом. Действующее значение силы тока:
Действующее значение силы тока:
Действующее значение напряжения:
Мощность в цепи переменного тока:
Трансформатор
Если напряжение на входе в трансформатор равно U1, а на выходе U2, при этом число витков в первичной обмотке равно n1, а во вторичной n2, то выполняется следующее соотношение:
Коэффициент трансформации вычисляется по формуле:
Если трансформатор идеальный, то выполняется следующее соотношение (мощности на входе и выходе равны):
В неидеальном трансформаторе вводится понятие КПД:
Волны
Длина волны может быть рассчитана по формуле:
Разность фаз колебаний двух точек волны, расстояние между которыми l:
Скорость электромагнитной волны (в т.ч. света) в некоторой среде:
Скорость электромагнитной волны (в т.ч. света) в вакууме постоянна и равна с = 3∙108 м/с, она также может быть вычислена по формуле:
Скорости электромагнитной волны (в т. ч. света) в среде и в вакууме также связаны между собой формулой:
ч. света) в среде и в вакууме также связаны между собой формулой:
При этом показатель преломления некоторого вещества можно рассчитать используя формулу:
Оптика
К оглавлению…
Оптическая длина пути определяется формулой:
Оптическая разность хода двух лучей:
Условие интерференционного максимума:
Условие интерференционного минимума:
Формула дифракционной решетки:
Закон преломления света на границе двух прозрачных сред:
Постоянную величину n21 называют относительным показателем преломления второй среды относительно первой. Если n1 > n2, то возможно явление полного внутреннего отражения, при этом:
Формула тонкой линзы:
Линейным увеличением линзы Γ называют отношение линейных размеров изображения и предмета:
Атомная и ядерная физика
К оглавлению. ..
..
Энергия кванта электромагнитной волны (в т.ч. света) или, другими словами, энергия фотона вычисляется по формуле:
Импульс фотона:
Формула Эйнштейна для внешнего фотоэффекта (ЗСЭ):
Максимальная кинетическая энергия вылетающих электронов при фотоэффекте может быть выражена через величину задерживающего напряжение Uз и элементарный заряд е:
Существует граничная частота или длинна волны света (называемая красной границей фотоэффекта) такая, что свет с меньшей частотой или большей длиной волны не может вызвать фотоэффект. Эти значения связаны с величиной работы выхода следующим соотношением:
Второй постулат Бора или правило частот (ЗСЭ):
В атоме водорода выполняются следующие соотношения, связывающие радиус траектории вращающегося вокруг ядра электрона, его скорость и энергию на первой орбите с аналогичными характеристиками на остальных орбитах:
На любой орбите в атоме водорода кинетическая (К) и потенциальная (П) энергии электрона связаны с полной энергией (Е) следующими формулами:
Общее число нуклонов в ядре равно сумме числа протонов и нейтронов:
Дефект массы:
Энергия связи ядра выраженная в единицах СИ:
Энергия связи ядра выраженная в МэВ (где масса берется в атомных единицах):
Формула альфа-распада:
Формула бета-распада:
Закон радиоактивного распада:
Ядерные реакции
Для произвольной ядерной реакции описывающейся формулой вида:
Выполняются следующие условия:
Энергетический выход такой ядерной реакции при этом равен:
Основы специальной теории относительности (СТО)
К оглавлению. ..
..
Релятивистское сокращение длины:
Релятивистское удлинение времени события:
Релятивистский закон сложения скоростей. Если два тела движутся навстречу друг другу, то их скорость сближения:
Релятивистский закон сложения скоростей. Если же тела движутся в одном направлении, то их относительная скорость:
Энергия покоя тела:
Любое изменение энергии тела означает изменение массы тела и наоборот:
Полная энергия тела:
Полная энергия тела Е пропорциональна релятивистской массе и зависит от скорости движущегося тела, в этом смысле важны следующие соотношения:
Релятивистское увеличение массы:
Кинетическая энергия тела, движущегося с релятивистской скоростью:
Между полной энергией тела, энергией покоя и импульсом существует зависимость:
Равномерное движение по окружности
К оглавлению…
В качестве дополнения, в таблице ниже приводим всевозможные взаимосвязи между характеристиками тела равномерно вращающегося по окружности (T – период, N – количество оборотов, v – частота, R – радиус окружности, ω – угловая скорость, φ – угол поворота (в радианах), υ – линейная скорость тела, an – центростремительное ускорение, L – длина дуги окружности, t – время):
Расширенная PDF версия документа «Все главные формулы по школьной физике»:
К оглавлению. ..
..
Что такое дельта с точки зрения математики?
Что такое дельта с точки зрения математики? Символ дельты: изменение
Дельта в верхнем регистре (Δ) в большинстве случаев означает «изменение» или «изменение» в математике. Рассмотрим пример, в котором переменная x обозначает движение объекта. Итак, «Δx» означает «изменение движения». Ученые используют это математическое значение дельты в различных областях науки.
Что означает этот символ ∆? ∆: Означает «изменение» или «разницу», как в уравнении наклона линии: 2. 1. 2.
Что означает Δ в исчислении? Строчная буква δ (или ) может использоваться для обозначения: Изменение значения переменной в исчислении. Функциональная производная в функциональном исчислении. Вспомогательная функция в исчислении, используемая для строгого определения предела или непрерывности данной функции.
Дельта означает вычитание? Греческая буква дельта означает «изменение». Это «изменение в» относится к изменению значения некоторой величины. Изменение рассчитывается путем вычитания более раннего значения количества из более позднего значения количества. Это вычитание может дать положительный, отрицательный или нулевой результат изменения.
Это «изменение в» относится к изменению значения некоторой величины. Изменение рассчитывается путем вычитания более раннего значения количества из более позднего значения количества. Это вычитание может дать положительный, отрицательный или нулевой результат изменения.
Как найти дельту в математике?
Если у вас есть случайная пара чисел и вы хотите узнать дельту — или разницу — между ними, просто вычтите меньшее из большего. Например, дельта между 3 и 6 равна (6 – 3) = 3. Если одно из чисел отрицательное, сложите два числа вместе.
Что означает этот символ в математике?
Этот символ < означает меньше, например, 2 означает больше, например, 4 > 2. ≤ ≥ Эти символы означают «меньше или равно» и «больше или равно» и обычно используются в алгебре.
Что значит ∆ по-гречески?
Греческая буква дельта (δ или ∆) часто используется для обозначения такого изменения. Если x является переменной, мы пишем δx для обозначения изменения значения x. Иногда мы называем δx приращением x.
Почему Дельта треугольник?
Дельта, названная в честь четвертой буквы греческого алфавита (в форме треугольника), представляет собой треугольную область, где крупная река делится на несколько более мелких частей, которые обычно впадают в более крупный водоем. Первой так называемой дельтой была дельта Нила, названная греческим историком Геродотом.
Что означает δ в физике?
В общей физике дельта-v — это изменение скорости. Греческая заглавная буква Δ (дельта) является стандартным математическим символом для обозначения изменения некоторой величины. В зависимости от ситуации delta-v может быть либо пространственным вектором (Δv), либо скаляром (Δv).
Означает ли дельта разницу?
Что означает дельта? Разница — наиболее распространенное значение дельты в верхнем регистре. Это просто разница или изменение в определенном количестве. Когда мы говорим дельта y, например, мы имеем в виду изменение y или то, насколько у изменяется.
Означает ли символ дельта изменение?
Символ дельты: изменение
Дельта в верхнем регистре (Δ) в большинстве случаев означает «изменение» или «изменение» в математике. Рассмотрим пример, в котором переменная x обозначает движение объекта. Итак, «Δx» означает «изменение движения». Ученые используют это математическое значение дельты в различных областях науки.
Рассмотрим пример, в котором переменная x обозначает движение объекта. Итак, «Δx» означает «изменение движения». Ученые используют это математическое значение дельты в различных областях науки.
Что такое дельта-краткий ответ?
Дельта представляет собой участок земли треугольной формы, расположенный в устье реки. Он образуется, когда река откладывает наносы по мере того, как течет к своему устью (место, где река впадает в озеро, море или океан).
Что означает дельта в бухгалтерском учете?
Что такое Дельта? Дельта — это коэффициент, который сравнивает изменение цены актива, обычно рыночных ценных бумаг, с соответствующим изменением цены его производного инструмента.
Что такое дельта в анализе данных?
Греческая буква дельта используется для обозначения разницы между двумя параметрами. За буквой может следовать некоторый пояснительный текст, обычно в виде подтекста, обозначающий тип разницы (например, относительная разница или абсолютная разница, а также, необязательно, переменные, для которых она вычисляется.
Что такое R* в математике?
В математике обозначение R* представляет два разных значения. В системе счисления R * определяет множество всех ненулевых действительных чисел, которые образуют группу при операции умножения. В функциях R* определяет рефлексивно-транзитивное замыкание бинарного отношения «R» в множестве.
Что такое математический язык и символы?
В математике символический язык — это язык, который использует символы или символы для представления понятий, таких как математические операции, выражения и операторы, а также объекты или операнды, над которыми выполняются операции.
Какие 24 греческие буквы?
Прописные и строчные формы двадцати четырех букв: Α α, β, Γ γ, Δ δ, ε ε, Ζ ζ, Η η, Θ θ, Ι ι, Κ κ, Λ λ, Μ μ, Ν ν, Ξ ξ, Ο ο, Π π, Ρ ρ, 2 σ/ς, Τ τ, Υ υ, Φ φ, Χ χ, Ψ ψ и Ω ω.
Что означает греческий поцелуй?
Греческий поцелуй — один из немногих стимуляторов анилингуса. Его формула с мятой может вызывать ощущение тепла в анальной области и индивидуально повышать чувствительность при оральном сексе. С дополнительным свежим ароматом для взаимного веселья.
С дополнительным свежим ароматом для взаимного веселья.
Что означает отрицательная дельта?
Положительная дельта означает, что у вас длинная позиция на рынке, а отрицательная дельта означает, что у вас короткая позиция на рынке.
Почему дельты называются дельтами?
Термин дельта происходит от заглавной греческой буквы дельта (Δ), которая имеет форму треугольника. Дельты с такой треугольной или веерной формой называются дугообразными (дугообразными) дельтами. Река Нил образует дугообразную дельту, впадая в Средиземное море.
Как ввести символ дельты?
Использование сочетания клавиш Alt для вставки символа Delta
Вы можете нажать клавишу Alt в сочетании с цифрами на цифровой клавиатуре, чтобы вставить символ дельты: Нажмите Alt + 235, чтобы ввести дельту нижнего регистра (δ). Нажмите Alt + 916, чтобы ввести верхний регистр или заглавную букву дельта (Δ)
В чем разница между ∆ и D?
В математике δ и Δ по существу относятся к одному и тому же, то есть к изменению. Это означает, что Δx=x1−x2=δx. Разница между δ и d также ясна и отчетлива в дифференциальном исчислении. Мы знаем, что dydx — это всегда оператор, а не дробь, тогда как δyδx — бесконечно малое изменение.
Это означает, что Δx=x1−x2=δx. Разница между δ и d также ясна и отчетлива в дифференциальном исчислении. Мы знаем, что dydx — это всегда оператор, а не дробь, тогда как δyδx — бесконечно малое изменение.
Что такое дельта в 11 классе физики?
Греческая заглавная буква дельта — это стандартный математический символ, обозначающий изменение некоторого количества или различия в чем-либо. delta-v — изменение скорости. Например, если переменная «х» обозначает движение объекта, то «Δх» означает изменение движения.
Что значит дельта на иврите?
Дельта — еврейское имя девушки, и значение этого имени — «Треугольное устье реки».
Что такое пример дельты?
Определение дельты — это отложение песка, глины или ила треугольной формы в устье реки. Примером дельты является место впадения реки Нил в Средиземное море. Обычно треугольная масса наносов, особенно ила и песка, отложенная в устье реки.
10 формул по физике
Доброго дня уважаемые радиолюбители!
Приветствую вас на сайте “Радиолюбитель“
Формулы составляют скелет науки об электронике. Вместо того, чтобы сваливать на стол целую кучу радиоэлементов, а потом переподключать их между собой, пытаясь выяснить, что же появится на свет в результате, опытные специалисты сразу строят новые схемы на основе известных математических и физических законов. Именно формулы помогают определять конкретные значения номиналов электронных компонентов и рабочих параметров схем.
Вместо того, чтобы сваливать на стол целую кучу радиоэлементов, а потом переподключать их между собой, пытаясь выяснить, что же появится на свет в результате, опытные специалисты сразу строят новые схемы на основе известных математических и физических законов. Именно формулы помогают определять конкретные значения номиналов электронных компонентов и рабочих параметров схем.
Точно так же эффективно использовать формулы для модернизации уже готовых схем. К примеру, для того, чтобы выбрать правильный резистор в схеме с лампочкой, можно применить базовый закон Ома для постоянного тока (о нем можно будет прочесть в разделе “Соотношения закона Ома” сразу после нашего лирического вступления). Лампочку можно заставить, таким образом, светить более ярко или, наоборот — притушить.
В этой главе будут приведены многие основные формулы физики, с которыми рано или поздно приходится сталкиваться в процессе работы в электронике. Некоторые из них известны уже столетия, но мы до сих пор продолжаем ими успешно пользоваться, как будут пользоваться и наши внуки.
Закон Ома представляет собой взаимное соотношение между напряжением, током, сопротивлением и мощностью. Все выводимые формулы для расчета каждой из указанных величин представлены в таблице:
| Искомая величина | Формула |
| Напряжение, В | U=I*R |
| Ток, А | I=U/R |
| Сопротивление, Ом | R=U/I |
| Мощность, Вт | P=U*I |
В этой таблице используются следующие общепринятые обозначения физических величин:
U — напряжение (В),
I — ток (А),
Р — мощность (Вт),
R — сопротивление (Ом),
Потренируемся на следующем примере: пусть нужно найти мощность схемы. Известно, что напряжение на ее выводах составляет 100 В, а ток— 10 А. Тогда мощность согласно закону Ома будет равна 100 х 10 = 1000 Вт. Полученное значение можно использовать для расчета, скажем, номинала предохранителя, который нужно ввести в устройство, или, к примеру, для оценки счета за электричество, который вам лично принесет электрик из ЖЭК в конце месяца.
Полученное значение можно использовать для расчета, скажем, номинала предохранителя, который нужно ввести в устройство, или, к примеру, для оценки счета за электричество, который вам лично принесет электрик из ЖЭК в конце месяца.
А вот другой пример: пусть нужно узнать номинал резистора в цепи с лампочкой, если известно, какой ток мы хотим пропускать через эту цепь. По закону Ома ток равен:
I = U / R
Схема, состоящая из лампочки, резистора и источника питания (батареи) показана на рисунке. Используя приведенную формулу, вычислить искомое сопротивление сможет даже школьник.
Что же в этой формуле есть что? Рассмотрим переменные подробнее.
> U пит (иногда также обозначается как V или Е): напряжение питания. Вследствие того, что при прохождении тока через лампочку на ней падает какое-то напряжение, величину этого падения (обычно рабочее напряжение лампочки, в нашем случае 3,5 В) нужно вычесть из напряжения источника питания. К примеру, если Uпит = 12 В, то U = 8,5 В при условии, что на лампочке падает 3,5 В.
К примеру, если Uпит = 12 В, то U = 8,5 В при условии, что на лампочке падает 3,5 В.
> I: ток (измеряется в амперах), который планируется пропустить через лампочку. В нашем случае – 50 мА. Так как в формуле ток указывается в амперах, то 50 миллиампер составляет лишь малую его часть: 0,050 А.
> R: искомое сопротивление токоограничивающего резистора, в омах.
В продолжение, можно проставить в формулу расчета сопротивления реальные цифры вместо U, I и R:
R = U/I = 8,5 В / 0,050 А= 170 Ом
Расчёты сопротивленияРассчитать сопротивление одного резистора в простой цепи достаточно просто. Однако с добавлением в нее других резисторов, параллельно или последовательно, общее сопротивление цепи также изменяется. Суммарное сопротивление нескольких соединенных последовательно резисторов равно сумме отдельных сопротивлений каждого из них. Для параллельного же соединения все немного сложнее.
Почему нужно обращать внимание на способ соединения компонентов между собой? На то есть сразу несколько причин.
> Сопротивления резисторов составляют только некоторый фиксированный ряд номиналов. В некоторых схемах значение сопротивления должно быть рассчитано точно, но, поскольку резистор именно такого номинала может и не существовать вообще, то приходится соединять несколько элементов последовательно или параллельно.
> Резисторы — не единственные компоненты, которые имеют сопротивление. К примеру, витки обмотки электромотора также обладают некоторым сопротивлением току. Во многих практических задачах приходится рассчитывать суммарное сопротивление всей цепи.
Расчет сопротивления последовательных резисторовФормула для вычисления суммарного сопротивления резисторов, соединенных между собой последовательно, проста до неприличия. Нужно просто сложить все сопротивления:
Rобщ = Rl + R2 + R3 + … (столько раз, сколько есть элементов)
В данном случае величины Rl, R2, R3 и так далее — сопротивления отдельных резисторов или других компонентов цепи, а Rобщ — результирующая величина.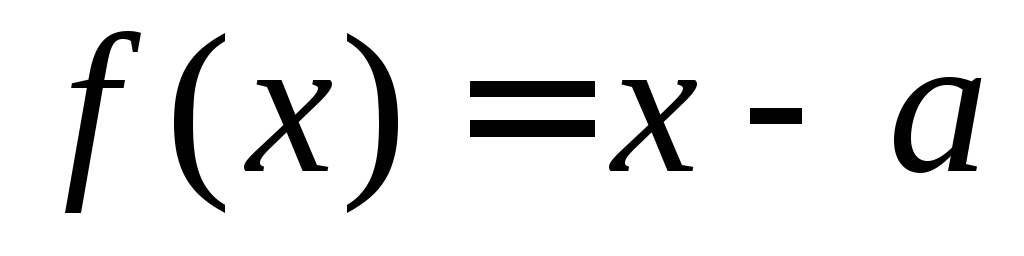
Так, к примеру, если имеется цепь из двух соединенных последовательно резисторов с номиналами 1,2 и 2,2 кОм, то суммарное сопротивление этого участка схемы будет равно 3,4 кОм.
Расчет сопротивления параллельных резисторовВсе немного усложняется, если требуется вычислить сопротивление цепи, состоящей из параллельных резисторов. Формула приобретает вид:
R общ = R1 * R2 / (R1 + R2)
где R1 и R2 — сопротивления отдельных резисторов или других элементов цепи, а Rобщ -результирующая величина. Так, если взять те же самые резисторы с номиналами 1,2 и 2,2 кОм, но соединенные параллельно, получим
776,47 = 2640000 / 3400
Для расчета результирующего сопротивления электрической цепи из трех и более резисторов используется следующая формула:
Здесь снова величины Rl, R2, R3 и так далее — сопротивления отдельных резисторов, a Rобщ — суммарная величина.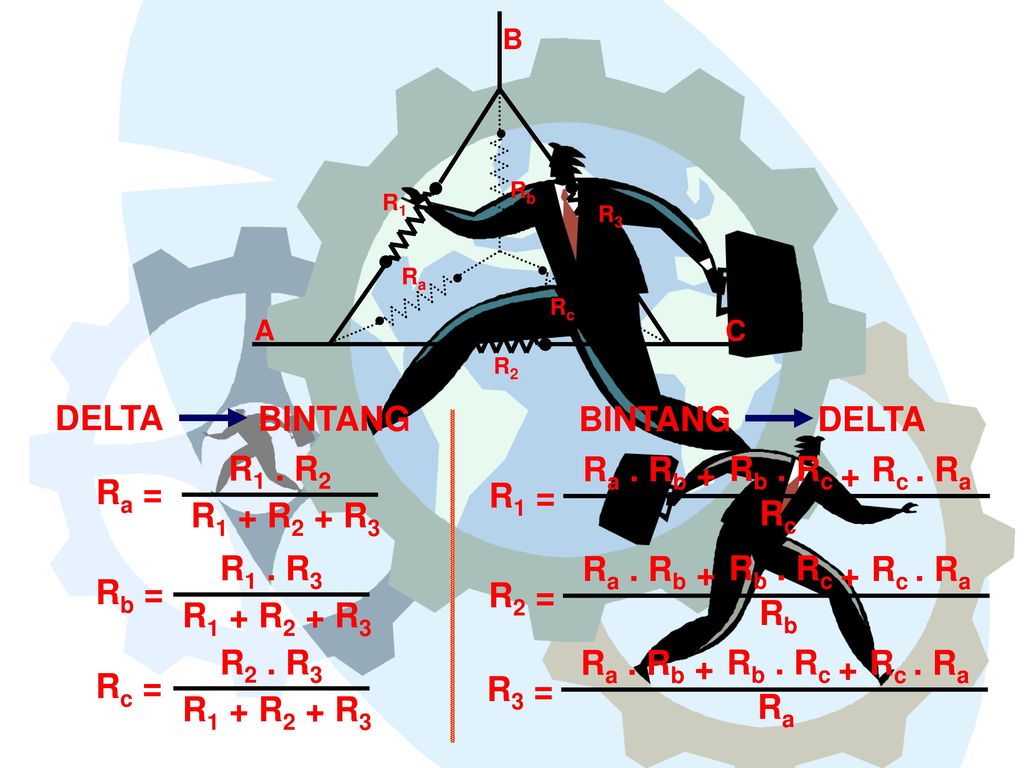
Формулы, приведенные выше, справедливы и для расчета емкостей, только с точностью до наоборот. Так же, как и для резисторов, их можно расширить для любого количества компонентов в цепи.
Расчет емкости параллельных конденсаторовЕсли нужно вычислить емкость цепи, состоящей из параллельных конденсаторов, необходимо просто сложить их номиналы:
Собщ = CI + С2 + СЗ + …
В этой формуле CI, С2 и СЗ — емкости отдельных конденсаторов, а Собщ суммирующая величина.
Расчет емкости последовательных конденсаторовДля вычисления общей емкости пары связанных последовательно конденсаторов применяется следующая формула:
Собщ = С1 * С2 /( С1+С2)
где С1 и С2 — значения емкости каждого из конденсаторов, а Собщ — общая емкость цепи
Расчет емкости трех и более последовательно соединенных конденсаторовВ схеме имеются конденсаторы? Много? Ничего страшного: даже если все они связаны последовательно, всегда можно найти результирующую емкость этой цепи:
И здесь опять величины C1, С2, СЗ и так далее — емкости отдельных конденсаторов, а Собщ.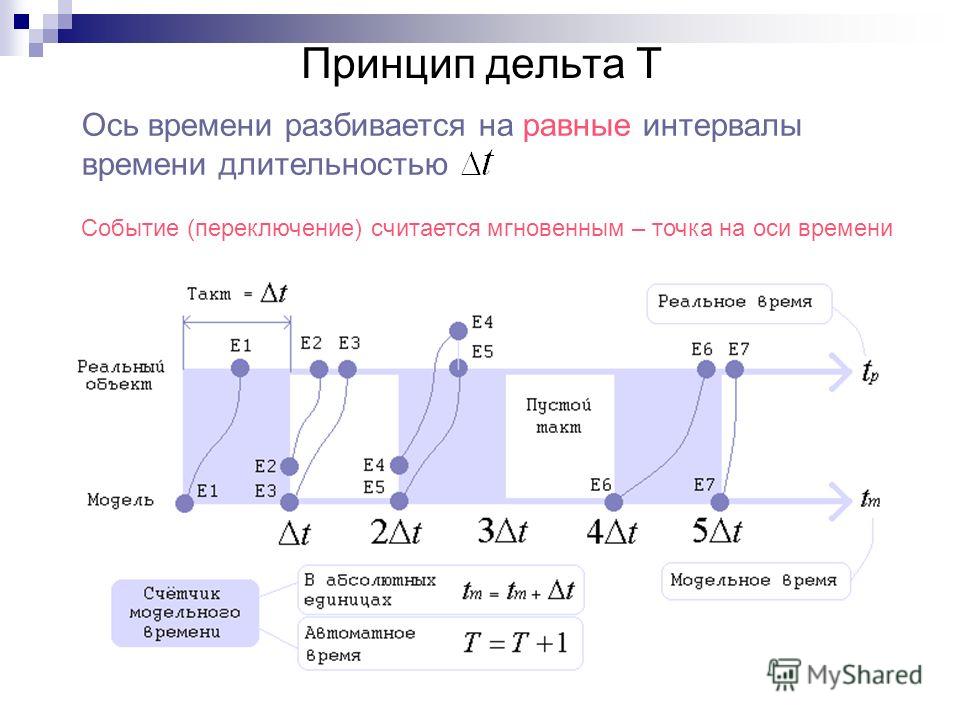 — суммарная величина.
— суммарная величина.
Так зачем же вязать последовательно сразу несколько конденсаторов, когда могло хватить одного? Одним из логических объяснений этому факту служит необходимость получения конкретного номинала емкости цепи, аналога которому в стандартном ряду номиналов не существует. Иногда приходится идти и по более тернистому пути, особенно в чувствительных схемах, как, например, радиоприемники.
Расчёт энергетических уравненийНаиболее широко на практике применяют такую единицу измерения энергии, как киловатт-часы или, если это касается электроники, ватт-часы. Рассчитать затраченную схемой энергию можно, зная длительность времени, на протяжении которого устройство включено. Формула для расчета такова:
ватт-часы = Р х Т
В этой формуле литера Р обозначает мощность потребления, выраженную в ваттах, а Т — время работы в часах. В физике принято выражать количество затраченной энергии в ватт-секундах, или Джоулях. Для расчета энергии в этих единицах ватт-часы делят на 3600.
Для расчета энергии в этих единицах ватт-часы делят на 3600.
В электронных схемах часто используются RC-цепочки для обеспечения временных задержек или удлинения импульсных сигналов. Самые простые цепочки состоят всего лишь из резистора и конденсатора (отсюда и происхождение термина RC-цепочка).
Принцип работы RC-цепочки состоит в том, что заряженный конденсатор разряжается через резистор не мгновенно, а на протяжении некоторого интервала времени. Чем больше сопротивление резистора и/или конденсатора, тем дольше будет разряжаться емкость. Разработчики схем очень часто применяют RC-цепочки для создания простых таймеров и осцилляторов или изменения формы сигналов.
Каким же образом можно рассчитать постоянную времени RC-цепочки? Поскольку эта схема состоит из резистора и конденсатора, в уравнении используются значения сопротивления и емкости. Типичные конденсаторы имеют емкость порядка микрофарад и даже меньше, а системными единицами являются фарады, поэтому формула оперирует дробными числами.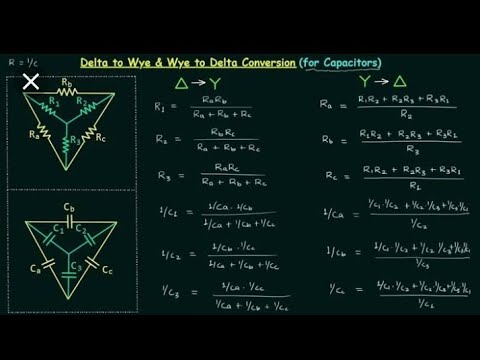
T = RC
В этом уравнении литера Т служит для обозначения времени в секундах, R — сопротивления в омах, и С — емкости в фарадах.
Пусть, к примеру, имеется резистор 2000 Ом, подключенный к конденсатору 0,1 мкФ. Постоянная времени этой цепочки будет равна 0,002 с, или 2 мс.
Для того чтобы на первых порах облегчить вам перевод сверхмалых единиц емкостей в фарады, мы составили таблицу:
| Значение емкости конденсатора, мкФ | Емкость конденсатора для расчета |
| 10 | 0,000 01 |
| 1 | 0,000 001 |
| 0,1 | 0,000 000 1 |
| 0,01 | 0,000 000 01 |
Частота сигнала является величиной, обратно пропорциональной его длине волны, как будет видно из формул чуть ниже. Эти формулы особенно полезны при работе с радиоэлектроникой, к примеру, для оценки длины куска провода, который планируется использовать в качестве антенны. Во всех следующих формулах длина волны выражается в метрах, а частота — в килогерцах.
Эти формулы особенно полезны при работе с радиоэлектроникой, к примеру, для оценки длины куска провода, который планируется использовать в качестве антенны. Во всех следующих формулах длина волны выражается в метрах, а частота — в килогерцах.
Предположим, вы хотите изучать электронику для того, чтобы, собрав свой собственный приемопередатчик, поболтать с такими же энтузиастами из другой части света по аматорской радиосети. Частоты радиоволн и их длина стоят в формулах бок о бок. В радиолюбительских сетях часто можно услышать высказывания о том, что оператор работает на такой-то и такой длине волны. Вот как рассчитать частоту радиосигнала, зная длину волны:
Частота = 300000 / длина волны
Длина волны в данной формуле выражается в миллиметрах, а не в футах, аршинах или попугаях. Частота же дана в мегагерцах.
Расчет длины волны сигналаТу же самую формулу можно использовать и для вычисления длины волны радиосигнала, если известна его частота:
Длина волны = 300000 / Частота
Результат будет выражен в миллиметрах, а частота сигнала указывается в мегагерцах.
Приведем пример расчета. Пусть радиолюбитель общается со своим другом на частоте 50 МГц (50 миллионов периодов в секунду). Подставив эти цифры в приведенную выше формулу, получим:
6000 миллиметров = 300000 / 50 МГц
Однако чаще пользуются системными единицами длины — метрами, поэтому для завершения расчета нам остается перевести длину волны в более понятную величину. Так как в 1 метре 1000 миллиметров, то в результате получим 6 м. Оказывается, радиолюбитель настроил свою радиостанцию на длину волны 6 метров. Прикольно!
Дельта-метод и его реализация в R
[Эта статья была впервые опубликована на The Princess of Science и любезно предоставлена R-блогерам]. (Вы можете сообщить о проблеме с содержанием на этой странице здесь)
Хотите поделиться своим контентом с R-блогерами? нажмите здесь, если у вас есть блог, или здесь, если у вас его нет.
Предположим, у вас есть выборка интересующей переменной, например. рост мужчин в определенной популяции, и по какой-то непонятной причине вас интересует не средний рост μ, а его квадрат μ². Как бы вы сделали вывод о μ², например. проверить гипотезу или рассчитать доверительный интервал? Дельта-метод — это то, что вам нужно.
рост мужчин в определенной популяции, и по какой-то непонятной причине вас интересует не средний рост μ, а его квадрат μ². Как бы вы сделали вывод о μ², например. проверить гипотезу или рассчитать доверительный интервал? Дельта-метод — это то, что вам нужно.
Дельта-метод — это математическое утверждение, которое может дать оценки дисперсии функций статистики при мягких условиях. Говоря лузли, пусть bₙ является оценкой β, где n — размер выборки, а распределение bₙ приблизительно нормальное со средним значением β и дисперсией σ²/n.
Тогда, если g является функцией, то g(bₙ) приблизительно нормальное значение со средним значением g(β) и дисперсией [g’(β)² ]⋅σ²/n при условии, что размер выборки велик. Пусть вас не пугает расчет. Функция deltmethod в R выполнит вычисления за вас.
Если bₙ – оценка максимального правдоподобия (MLE) для β, то в мягких условиях она является приблизительно нормальной для большого размера выборки, а g(bₙ) и g'(bₙ) – это MLE для g(β) и g'( β) соответственно. Добавьте к этому MLE для σ, и вы сможете реализовать статистический вывод.
Добавьте к этому MLE для σ, и вы сможете реализовать статистический вывод.
Я продемонстрирую использование дельта-метода, используя данные о выживании Титаника. Для примера я буду использовать только 3 переменные: Survived — это переменная 0/1, указывающая, выжил ли пассажир во время крушения Титаника, Age — это, очевидно, возраст пассажира, а Parch — это количество родителей/детей пассажира на борту. Давайте посмотрим на некоторые данные:
> # install.packages("титаник")
> библиотека (титаник)
> titanic=titanic_train[ c(1, 2, 6,8)]
> голова (титаник)
PassengerId Survived Age Parch
1 1 0 22 0
2 2 1 38 0
3 3 1 26 0
4 4 1 35 0
5 5 0 35 0
6 6 0 NA 0
> Пусть π будет вероятностью выживания. Тогда шансы на выживание равны π/(1-π). Размер выборки n = 89.1 считается большим, поэтому мы можем применить Центральную предельную теорему, чтобы заключить, что p является приблизительно нормальным со средним значением π и дисперсией π/(1-π)/n. Тогда π можно оценить как p=0,384, шансы оценить как p/(1-p)=0,623, а дисперсия p оценить как 0,000265:
Тогда π можно оценить как p=0,384, шансы оценить как p/(1-p)=0,623, а дисперсия p оценить как 0,000265:
> p_survival=mean(titanic$Survived) > распечатать (p_survival) [1] 0,3838384 > survival_odds=p_survival/(1-p_survival) > распечатать (выживание_шансы) [1] 0,6229508 > n=nrow(титанический) > var_p_survival=(p_survival*(1-p_survival))/n > распечатать (var_p_survival) [1] 0,0002654392)*var_p_survival > распечатать (var_odds) [1] 0,01313328 > se_odds=sqrt(var_odds) > распечатать (se_odds) [1] 0,1146005 >
Но, конечно, вместо того, чтобы выполнять все вычисления, вы можете использовать функцию deltamethod пакета R msm.
Функция имеет три параметра:
- g — объект-формула, представляющий преобразование g( x ). Переменные формулы должны быть помечены x1, x2 и так далее.
- означает оценку g(β)
- cov — это оценка var(β), которая равна σ²/n
Использование дельта-функции дает тот же результат:
> # install.packages("msm") > библиотека (мсм) > se_odds_delta=deltamethod(g=~x1/(1-x1), mean=survival_odds, cov=var_p_survival) > распечатать (se_odds_delta) [1] 0,1146005 >
Во втором примере рассматривается логистическая регрессия. Мы будем моделировать (логарифмическую) вероятность выживания, используя Age nd Parch. Используя функцию glm R, мы можем получить оценки для коэффициентов логистической регрессии и их стандартных ошибок se_b:
> модель = glm (выжил ~ возраст + парч, семья = биномиальная (ссылка = "logit")
> model_beta=data.frame(резюме(модель)$коэффициенты[2:3, 1:2])
> имена(model_beta)=c("b", "se_b")
> печать (модель_бета)
б se_b
Возраст -0,0087 0,005421838
Парч 0,1
303 0,0635
>
Поскольку exp (β) обычно интерпретируется как отношение шансов (OR) переменной отклика относительно независимой переменной регрессии, исследователи заинтересованы в выводах о эксп (β). Чтобы сделать такой вывод, необходимо оценить стандартную ошибку exp (β). Поскольку b является оценкой максимального правдоподобия для β, она приблизительно нормальна, а ее дисперсия оценивается как se_b², и можно применять дельта-метод.
Поскольку b является оценкой максимального правдоподобия для β, она приблизительно нормальна, а ее дисперсия оценивается как se_b², и можно применять дельта-метод.
Расчет в этом случае прост: g( x ) = exp ( x ), поэтому g'( x ) = exp ( x ). Таким образом, стандартную ошибку exp (β) можно оценить как exp (b)⋅ se_b:
> model_beta$OR=exp(model_beta$b) > model_beta$se_OR=exp(model_beta$b)*model_beta$se_b > печать (модель_бета) б se_b ИЛИ se_OR Возраст -0,00870,005421838 0,9
9 0,005374374 Парч 0,1
303 0,0635 1,2111027 0,109778755 >
Чтобы использовать функцию дельта-метода, мы сначала воспользуемся функцией vcov для получения матрицы дисперсии-ковариации оценок коэффициента регрессии, а дисперсии будут входными данными функции дельта-метода:
> vc=vcov(модель)[2:3, 2:3] > печать (ВК) Возраст Парч Возраст 2,939632e-05 9,236876e-05 Парч 9.236876e-05 8.216269e-03 > model_beta$se_OR_delta[1]=deltamethod(~exp(x1), mean=model_beta$b[1], cov=vc[1,1]) > model_beta$se_OR_delta[2]=deltamethod(~exp(x1), mean=model_beta$b[2], cov=vc[2,2]) > печать (модель_бета) b se_b ИЛИ se_OR se_OR_delta Возраст -0,0087
0,005421838 0,9
9 0,005374374 0,005374374 Парч 0,1
303 0,0635 1,2111027 0,109778755 0,109778755 >
Разумеется, мы получаем те же результаты.
К оставьте комментарий для автора, пройдите по ссылке и оставьте комментарий в их блоге: Принцесса науки .
R-bloggers.com предлагает ежедневных обновления по электронной почте новостей R и руководств по изучению R и многим другим темам. Нажмите здесь, если вы хотите опубликовать или найти работу R/data-science. 9{r}$ по согласным производным | Достижения в непрерывных и дискретных моделях
- Исследования
- Открытый доступ
- Опубликовано:
- FAHD JARAD 1 ,
- Яссин Адбаби 2 ,
- Dumitru Baleanu 1,3 и
- …
- 44444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444one0047
Успехи в разностных уравнениях том 2018 , Номер статьи: 407 (2018) Процитировать эту статью
4203 Доступы
11 цитирований
- 9{r}\) для любого \(r\in \mathbb{R}\).

Введение
Ученые столкнулись с некоторыми трудностями при описании сложных систем с помощью классического исчисления. Чтобы преодолеть эти трудности, некоторые ученые начали использовать дробное исчисление, изучающее интегрирование и дифференцирование любого порядка. См., например, [1, 2] и ссылки в них. Обычные дробные производные, такие как Римана-Лиувилля, Капуто, Адамара и Грюнвальда-Летникова, нашли многочисленные применения в науке и технике, давая эффекты памяти и наследственности. Так называемая производная Хаусдорфа или фрактальная производная (см. [3, 4] и ссылки в них) также являются производными, которые можно использовать для описания сложных систем. Другие производные, такие как конформные производные, которые были введены в [5, 6], также могут быть кандидатами для использования для описания сложных явлений реального мира.
С другой стороны, степени функций распределения играют важную роль в различных разделах прикладной математики и физики (см.
 {\lambda})\) для некоторых значений 9{+\infty}\delta_{n} ( x ) \phi ( x ) \,dx=\phi ( 0 ) , $$
{\lambda})\) для некоторых значений 9{+\infty}\delta_{n} ( x ) \phi ( x ) \,dx=\phi ( 0 ) , $$(2)
где \(\delta_{n} ( x ) \) представляет собой последовательность обычных (классических) функций. Такая последовательность упоминается как дельта-сходящаяся последовательность или просто δ -последовательность. Для данной δ -последовательности \(\ delta _ {n} ( x ) \) мы имеем то, что известно как предельное представление δ -функции
$$ \дельта (х) =\lim_{n\стрелка вправо\infty}\delta_{n} (х) . $$
(3) 9{2}/4\bigr) $$
(5)
есть δ -последовательность в n так, что
$$ \lim_{n\стрелка вправо\infty}\delta_{n} ( m,x ) =\delta ( x ) . $$
Эти функции удовлетворяют
$$ \delta_{n} ( m,0 ) =0\quad \text{для всех }n\in \mathbb{N}. $$
В любой другой точке x последовательность также стремится к нулю. Тем не менее последовательность порождает δ -функцию. Известные предельные представления δ -функции включают дельта-последовательности, которые не обращаются в нуль на носителе предельной δ -функции.
 Однако в [18] Галапон предполагает, что δ -последовательность может обращаться в нуль на носителе предельной δ -функции для всех конечных значений предельного параметра. Определить произведения двух произвольных распределений в общем случае не представляется возможным [17, 19]. Однако произведение бесконечно дифференцируемой функции \(\phi ( x ) \) с распределением g определяется выражением
9{(n+1)}(x)\).
Однако в [18] Галапон предполагает, что δ -последовательность может обращаться в нуль на носителе предельной δ -функции для всех конечных значений предельного параметра. Определить произведения двух произвольных распределений в общем случае не представляется возможным [17, 19]. Однако произведение бесконечно дифференцируемой функции \(\phi ( x ) \) с распределением g определяется выражением
9{(n+1)}(x)\).Обобщенная формула Тейлора и теорема Тейлора в репере согласных производных приведены в следующих теоремах.
Теорема 7
([5])
Предположим, что г бесконечно α — дифференцируемая функция для некоторых \(0<\альфа\leq1\) в окрестности точки и . Затем г 9{\ гидроразрыва {1} {\ альфа}} \), \ (R> 0 \).
Далее, следуя Ван дер Корпуту [15], мы определяем нейтрикс как класс пренебрежимо малых функций, определенных в области, которые удовлетворяют следующим двум условиям:
- (я)
нейтрикс представляет собой аддитивную группу;
- (ii)
не содержит констант кроме 0.
 9{\mu}n, \quad \lambda>0, \mu =1,2,3,\ldots, $$
9{\mu}n, \quad \lambda>0, \mu =1,2,3,\ldots, $$(12)
и все они являются функциями, которые сходятся к нулю в обычном смысле как n стремится к бесконечности. Дополнительные математические свойства нейтриц и нейтричного предела можно найти в [15]. Обратите внимание, что взятие нейтриксного предела функции \(g (n) \) эквивалентно взятию обычного предела конечной части Адамара \(g (n) \). В [9] авторы использовали нейтриксный предел для определения степени δ -функции и ее производных как 9{ ( 2k ) } ( x ) $$
для всех \(k=0,1,2,\ldots \) . Это завершает доказательство. □
Замечание 17
Отметим, что теорема 16 является обобщением теоремы 10, полученной в [9], где в основном обсуждается случай для \(r\in \mathbb{R} \). В обеих теоремах четные степени \(\delta(x)\) оказываются равными нулю, а нечетные степени выражаются в виде постоянного кратного производной от \(\delta(x)\).
Завершим этот раздел следующим примером. 9{2}-6 ( 3+2m ) r+8 \bigr) [ h_{21}+h_{22} ] , $$
где
$$\begin{aligned}& h_{21} = r ( m+1 ) \varGamma \bigl( ( m+1/2 ) r \bigr) \operatorname{hypergeom} \bigl( [ 1+r ] , \bigl[ 2+ ( m+3/2 ) r \bigr] ,mr \bigr) , \\& h_{22} = \bigl( 1+ ( m+1/2 ) r \bigr) \varGamma \ bigl( ( m+1/2 ) r \bigr) \operatorname{hypergeom} \bigl( [ r ] , \bigl[ 2+ ( m+3/2 ) r \bigr] ,mr \bigr) , \end{ выровнено}$$
и
$$\begin{align}& v_{3} = \frac{3}{2} \biggl( -\frac{1}{mr} \biggr) ^{\frac{1}{2}+r }\varGamma ( -r ) \varGamma \bigl( ( m+3/2 ) r \bigr) \biggl( r- \frac{2}{3} \biggr) \bigl( 1+ ( m+3/2 ) r \bigr) ( r-2 ) h_{3}, \\& h_{3} = \operatorname{hypergeom} \bigl( \bigl[ — ( m+1/2 ) r \bigr] , \bigl[ 3- ( m+3/2 ) r \bigr] ,mr \bigr) , \end{aligned}$$ 9{3}\bigr) \bigr)=3\phi ( 0 ) .
 $$
$$Замечание 24
(49) найдено в [8] и [22], а (50) найдено в [22].
Замечание 25
Отметим, что теорема 22 является обобщением теоремы 10, полученной в [9], где в основном обсуждается случай \(r\in \mathbb{R} \).
Мы хотели бы упомянуть, что можно также найти \(\ln(\delta(x))\), используя δ -последовательность и предел нейтрикс, чтобы получить следующее тождество:
9{2m},\phi(x) \biggr) . \end{aligned}$$Заключение
Степени дельта-функции и ее производных имеют потенциальное применение в элементарной физике и квантовой механике. Кроме того, найти такие силы — сложная задача. В этой рукописи мы использовали определенную δ -последовательность, пределы нейтрикс и конформные производные для определения степени функции δ и ее производных. Некоторые результаты, полученные в рукописи, являются обобщением некоторых результатов, найденных в литературе. Однако было бы очень интересно, если бы недавно введенные дробные производные с неособыми ядрами использовались для определения степеней δ -функция.

Каталожные номера
Килбас, А., Шривастава, Х.М., Трухильо, Дж.Дж.: Теория и приложения дробных дифференциальных уравнений. Эльзевир, Амстердам (2006)
МАТЕМАТИКА Google ученый
Подлубный И.: Дробные дифференциальные уравнения. Академическая пресса, Сан-Диего (1999)
МАТЕМАТИКА Google ученый
Чен В.: Пространственно-временная ткань, лежащая в основе аномальной диффузии. Хаос Солитоны Фракталы 28 , 923–929 (2006)
Артикул Google ученый
Чен В., Лян Ю.: Новые методологии моделирования дробных и фрактальных производных. Хаос солитоны фракталы 102 , 72–77 (2017)
MathSciNet Статья Google ученый
«>
Абдельджавад, Т .: Об исчислении согласных дробей. Дж. Вычисл. заявл. Мат. 279 , 57–66 (2015)
MathSciNet Статья Google ученый
Халил, Р., Аль Хорани, М., Юсеф, А., Сабабхе, М.: Новое определение дробной производной. Дж. Вычисл. заявл. Мат. 264 , 65–70 (2014)
MathSciNet Статья Google ученый 9{р}\). Мат. Нахр. 157 , 243–248 (1992)
MathSciNet Статья Google ученый
Озчаг, Э.: Определение k -й степени дельта-распределения Дирака для отрицательных целых чисел. заявл. Мат. лат. 14 , 419–423 (2001)
MathSciNet Статья Google ученый
Ли, К.К.: Степени дельта-функции Дирака по дробным производным Капуто. Дж. Фракт. Расчет заявл.
 7 (1), 12–23 (2016)
7 (1), 12–23 (2016)MathSciNet Google ученый
Чанг, В.С.: Дробная механика Ньютона с дробно-согласными производными. Дж. Вычисл. заявл. Мат. 290 , 150–158 (2015)
MathSciNet Статья Google ученый
Чжао Д., Луо М.: Общая созвучная дробная производная и ее физическая интерпретация. Кальколо 54 , 903–917 (2017)
MathSciNet Статья Google ученый
Аль-Рифае, М., Абдельджавад, Т.: Фундаментальные результаты согласованных задач Штурма – Лиувилля на собственные значения. Сложность 2017 , Артикул ID 3720471 (2017)
MathSciNet МАТЕМАТИКА Google ученый
ван дер Корпут, Дж. Г.: Введение в нейтричное исчисление.
 Дж. Анал. Мат. 7 , 291–398 (1959–60)
Дж. Анал. Мат. 7 , 291–398 (1959–60)Канвал, Р.П.: Обобщенные функции: теория и техника, 2-е изд. Биркхойзер, Базель (1998)
МАТЕМАТИКА Google ученый
Гельфанд И.М., Шилов Г.Е. Обобщенные функции. 1. Академик Пресс, Нью-Йорк (1964).
Google ученый
Галапон, Э.А.: Дельта-сходящиеся последовательности, которые исчезают при поддержке предельной дельта-функции Дирака. Дж. Физ. А, мат. Теор. 42 , 175201 (2009)
MathSciNet Статья Google ученый
Антосик, П.: Состав раздачи. Технический отчет № 9 (1988–89)
ван дер Корпут, Дж. Г.: Neutrices. Дж. Соц. инд. заявл. Мат. 7 (3), 253–279 (1959)
MathSciNet Статья Google ученый
«>
Абрамовиц, М., Стегун, И.А.: В: Справочник по математическим функциям с формулами, графиками и математическими таблицами. заявл. Мат. Серия, вып. 55. Довер, Нью-Йорк (1964)
МАТЕМАТИКА Google ученый
- (я)
Фишер, Б.: Распределения и замена переменной. Бык. Мат. соц. науч. Мат. рум. 19(67) (1–2), 11–20 (1975)
MathSciNet МАТЕМАТИКА Google ученый
Математический факультет, факультет искусств и наук, Университет Чанкая, Анкара, Турция
Фахд Джарад и Дмитрий Балеану
Математический факультет Университета Боугхама Махмеда 4 , Бумердес, АлжирИнститут космических наук, Магуреле, Бухарест, Румыния
Думитру Балеану
Факультет математики и общих наук Университета принца Султана, Эр-Рияд, Королевство Саудовская Аравия
Thabet Abdeljawad
- Fahd Jarad
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Yassine Adjabi
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Академия
- Дмитрий Балеану
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- Thabet Abdeljawad
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Ссылки на скачивание
Наличие данных и материалов
Неприменимо.
Финансирование
Четвертый автор хотел бы поблагодарить Университет принца Султана за финансирование этой работы через исследовательскую группу «Методы нелинейного анализа в прикладной математике» (NAMAM), номер группы RG-DES-2017-01-17.
Информация об авторе
Авторы и организации
Яссин Аджаби
Авторы
Contributions
Авторы внесли равный вклад в статью. Все авторы прочитали и одобрили окончательный вариант рукописи.
Все авторы прочитали и одобрили окончательный вариант рукописи.
Автор, ответственный за переписку
Связь с Фахд Джарад.
Заявление об этике
Конкурирующие интересы
Авторы заявляют об отсутствии конкурирующих интересов.
Дополнительная информация
Примечание издателя
Springer Nature остается нейтральной в отношении юрисдикционных претензий в опубликованных картах и институциональной принадлежности.
Права и разрешения
Открытый доступ Эта статья распространяется на условиях международной лицензии Creative Commons Attribution 4.0 (http://creativecommons.org/licenses/by/4.0/), которая разрешает неограниченное использование, распространение, и воспроизведение на любом носителе, при условии, что вы укажете автора(ов) оригинала и источник, предоставите ссылку на лицензию Creative Commons и укажете, были ли внесены изменения.
Перепечатки и разрешения
Об этой статье
Как оценить стандартную ошибку преобразованных параметров регрессии в R с помощью дельта-метода?
Целью этой страницы является введение оценки стандартных ошибок с использованием дельта-метода. Примеры включают ручной расчет стандартных ошибок с помощью дельта-метода, а затем подтверждение с использованием функции
Примеры включают ручной расчет стандартных ошибок с помощью дельта-метода, а затем подтверждение с использованием функции дельта-метода , чтобы читатель мог понять расчеты и знать, как использовать дельтаметод .
На этой странице используются следующие пакеты Убедитесь, что вы можете загрузить их, прежде чем пытаться запускать примеры на этой странице. Нам понадобится пакет msm для использования функции deltamethod . Если у вас не установлен пакет, запустите: install.packages("packagename") , или если вы видите, что версия устарела, запустите: update.packages() .
библиотека (msm)
Информация о версии: Код для этой страницы был протестирован в версии R 3.1.1 (10 июля 2014 г.)
Дата: 01.08.2014
С: пекод 0,0-3; мсм 1,4; фиа 0,1-5; эффекты 3.0-0; цветовое пространство 1.2-4; RColorBrewer 1.0-5; таблица 1.7-3; автомобиль 2,0-20; зарубежный 0,8-61; Нмск 3. 14-4; Формула 1.1-2; выживаемость 2,37-7; решетка 0,20-29; мгкв 1,8-1; № 3.1-117; png 0,1-7; сеткаЭкстра 0.9.1; изменить форму2 1.4; ggplot2 1.0.0; вкд 1.3-1; ржсон 0.2.14; RSQLite 0.11.4; ДБИ 0,2-7; вязалка 1.6
14-4; Формула 1.1-2; выживаемость 2,37-7; решетка 0,20-29; мгкв 1,8-1; № 3.1-117; png 0,1-7; сеткаЭкстра 0.9.1; изменить форму2 1.4; ggplot2 1.0.0; вкд 1.3-1; ржсон 0.2.14; RSQLite 0.11.4; ДБИ 0,2-7; вязалка 1.6
Предыстория дельта-метода
Часто в дополнение к сообщениям о параметрах, соответствующих модели, нам необходимо сообщать
некоторое преобразование этих параметров. Преобразование может генерировать
точечные оценки наших желаемых значений, но стандартный
ошибки этих точечных оценок вычислить не так просто. Они могут,
однако будь
хорошо аппроксимируется дельта-методом. Дельта-метод аппроксимирует стандартные ошибки преобразования случайной величины с использованием тейлоровского приближения первого порядка. Коэффициенты регрессии сами по себе являются случайными величинами, поэтому мы можем использовать дельта-метод для аппроксимации стандартных ошибок их преобразований. Хотя дельта-метод часто уместно использовать с большими выборками, эта страница ни в коем случае не является одобрением использования дельта-метода по сравнению с другими методами для оценки стандартных ошибок, таких как бутстрэппинг. T Cov(X) \nabla G(\mu_X) $$.
T Cov(X) \nabla G(\mu_X) $$.
Пример 1: Скорректированный прогноз
Скорректированные прогнозы или скорректированные средние значения — это прогнозируемые значения отклика, рассчитанные для набора значений ковариат. Например, мы можем получить прогнозируемое значение «среднего» респондента, вычислив прогнозируемое значение как среднее значение всех ковариат. Скорректированные прогнозы являются функциями коэффициентов регрессии, поэтому мы можем использовать дельта-метод для аппроксимации их стандартных ошибок.
Мы хотели бы рассчитать стандартную ошибку скорректированного прогноза г в среднем х, 5,5, из линейной регрессии г на х :
х <- 1:10 среднее (х)
## [1] 5,5
у <- с(1,3,3,4,5,7,7,8,9,10) m1 <- lm(y~x) резюме (м1)
## ## Вызов: ## lm(формула = y ~ x) ## ## Остатки: ## Мин. 1 кв. Медиана 3 кв. Макс. ## -0,3636 -0,2455 -0,1273 -0,0455 0,8182 ## ## Коэффициенты: ## Оценить стандарт.Значение ошибки t Pr(>|t|) ## (Перехват) 0,4000 0,2949 1,36 0,21 ## x 0,9636 0,0475 20,27 3,7e-08 *** ## --- ## Значение. коды: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 '' 1 ## ## Остаточная стандартная ошибка: 0,432 на 8 степенях свободы ## Множественный R-квадрат: 0,981, скорректированный R-квадрат: 0,979 ## F-статистика: 411 на 1 и 8 DF, p-значение: 3,66e-08
Прогнозируемое значение y при x = 5,5 просто: $y=b_0 + 5,5b_1$. Мы можем думать о y как функция коэффициентов регрессии, или \(G(B)\):
$$ G(B) = b_0 + 5,5 b_1 $$
Таким образом, нам нужно получить вектор частных производных G( B) и ковариационная матрица B . Частные производные в этом случае очень легко вычислить вручную: \(\frac{dG}{db_0} = 1\) и \(\frac{dG}{db_1} = 5,5\).
град <- с(1, 5.5)
Мы можем легко получить ковариационную матрицу B , используя vcov на объект модели.
vb <- vcov(m1) о.б.
## (перехват) x ## (Перехват) 0,0870 -0,01242 ## х -0,0124 0,00226
Наконец, мы можем аппроксимировать стандартную ошибку, используя приведенную выше формулу.
vG <- t(град) %*% vb %*% град кврт(ВГ)
## [1] ## [1,] 0,137
Оказывается, функция прогнозирует с se.fit=T вычисляет стандартные ошибки дельта-метода, поэтому мы можем сравнить наши расчеты с расчетами из предсказывает .
прогнозировать (m1, newdata = data.frame (x = 5,5), se.fit = T)
## $подходит ## 1 ## 5.7 ## ## $se.fit ## [1] 0,137 ## ## $дф ## [1] 8 ## ## $остаток.масштаб ## [1] 0,432
Похоже, наши ручные вычисления хороши!
Теперь, когда мы поняли, как вручную вычислять стандартные ошибки дельта-метода, мы готовы использовать функцию deltamethod в msm упаковка. Функция deltamethod ожидает как минимум 3 аргумента. Первый аргумент — это формула, представляющая функцию, в которой все переменные должны быть помечены как x1, x2 и т. д. Второй аргумент — это средние значения переменных. Напомним, что \(G(B)\) является функцией коэффициентов регрессии, средние значения которых являются самими коэффициентами. \(G(B)\) не является прямой функцией предикторов. Третий аргумент — ковариационная матрица коэффициентов. По умолчанию
Первый аргумент — это формула, представляющая функцию, в которой все переменные должны быть помечены как x1, x2 и т. д. Второй аргумент — это средние значения переменных. Напомним, что \(G(B)\) является функцией коэффициентов регрессии, средние значения которых являются самими коэффициентами. \(G(B)\) не является прямой функцией предикторов. Третий аргумент — ковариационная матрица коэффициентов. По умолчанию дельтаметод вернет стандартные ошибки \(G(B)\), хотя вместо этого можно запросить ковариацию \(G(B)\) через четвертый аргумент.
дельтаметод(~ x1 + 5,5*x2, коэфф(m1), vcov(m1))
## [1] 0,137
Успех!
Обратите внимание, что в этом примере, поскольку \(G(B)\) является линейной функцией, дельта-метод не является точным методом и не является приближением.
Пример 2: Отношение шансов
Пример 1 несколько тривиален, учитывая, что предсказывает 9Функция 1769 вычисляет стандартные ошибки дельта-метода для скорректированных прогнозов. Действительно, если вам нужны только стандартные ошибки для скорректированных прогнозов либо по шкале линейного предиктора, либо по шкале переменной отклика, вы можете использовать
Действительно, если вам нужны только стандартные ошибки для скорректированных прогнозов либо по шкале линейного предиктора, либо по шкале переменной отклика, вы можете использовать для прогнозирования и пропустить ручные вычисления. Однако другие преобразования коэффициентов регрессии, которые предсказывает , не могут быть легко обработаны, часто полезны для отчета. Одним из таких преобразований является выражение коэффициентов логистической регрессии в виде отношения шансов. Поскольку отношения шансов представляют собой простые нелинейные преобразования коэффициентов регрессии, мы можем использовать дельта-метод для получения их стандартных ошибок.
В следующем примере мы моделируем вероятность зачисления в программу с отличием (незачисленных против зачисленных), прогнозируемую по полу, результатам по математике и чтению. Здесь мы читаем данные и используем фактор , чтобы объявить уровни почестей таким образом, чтобы была смоделирована вероятность «зачисления» (R будет моделировать вероятность последнего уровня фактора). Мы запустим нашу логистическую регрессию, используя
Мы запустим нашу логистическую регрессию, используя glm с family=binomial .
d <- read.csv("https://stats.idre.ucla.edu/stat/data/hsbdemo.csv")
d$honors <- factor(d$honors, level=c("не зачислен", "зачислен"))
m3 <- glm (почести ~ женщина + математика + чтение, данные = d, семья = бином)
резюме (м3)
## ## Вызов: ## glm(формула = отличие ~ женщина + математика + чтение, семья = бином, ## данные = г) ## ## Остаточное отклонение: ## Мин. 1 кв. Медиана 3 кв. Макс. ## -2,006 -0,606 -0,273 0,484 2,395 ## ## Коэффициенты: ## Оценить стандарт. Значение ошибки z Pr(>|z|) ## (Перехват) -11,9727 1,7387 -6,89 5,7e-12 *** ## самка самец -1,1548 0,4341 -2,66 0,0078 ** ## математика 0.1317 0.0325 4.06 5.0e-05 *** ## чтение 0,0752 0,0276 2,73 0,0064 ** ## --- ## Значение. коды: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 '' 1 ## ## (Параметр дисперсии для биномиального семейства принимается равным 1) ## ## Нулевое отклонение: 231,29на 199 степеней свободы ## Остаточное отклонение: 150,42 на 196 степенях свободы ## АИК: 158,4 ## ## Количество итераций оценки Фишера: 5
В выходных данных выше коэффициенты регрессии выражены в логарифмической шкале шансов (линейный предиктор). Чтобы выразить их как отношения шансов, мы просто возводим коэффициенты в степень. Давайте посмотрим на математический коэффициент, выраженный как отношение шансов:
Чтобы выразить их как отношения шансов, мы просто возводим коэффициенты в степень. Давайте посмотрим на математический коэффициент, выраженный как отношение шансов:
b2 <- coef(m3)[3] ехр(b2)
## математика ## 1.14
Таким образом, на каждую единицу повышения по математике мы ожидаем 14-процентное увеличение шансов быть зачисленным в программу с отличием.
Мы можем использовать ту же процедуру, что и раньше, для расчета стандартной ошибки дельта-метода. Сначала мы определяем функцию преобразования, здесь простое возведение в степень коэффициента для математики:
$$ G(B) = \exp(b_2) $$
Градиент снова очень легко получить вручную — производная от \( \exp(X)\) равно \(\exp(X)\) - поэтому \(\nabla G(B) = \exp(b_2)\):
град <- exp(b2) выпускник
## математика ## 1.14
Поскольку наше преобразование включает только математический коэффициент, нам не нужна вся ковариационная матрица всех параметров регрессии. Нам нужна только дисперсия математического коэффициента:
Нам нужна только дисперсия математического коэффициента:
# не хочу этого вков (м3)
## (Перехват) женщина мужчина чтение математики ## (Перехват) 3,0230 0,10703 -0,035147 -0,018085 ## самкамужчина 0,1070 0,18843 -0,001892 -0,001287 ## математика -0,0351 -0,00189 0,001054 -0,000427 ## чтение -0,0181 -0,00129 -0,000427 0,000761
#хочу это вместо этого vb2 <- vcov(m3)[3,3] vb2
## [1] 0,00105
Наконец, мы готовы вычислить стандартную ошибку дельта-метода
vG <- grad %*% vb2 %*% grad кврт(ВГ)
## [1] ## [1,] 0,037
Давайте подтвердим наши выводы с помощью deltamethod :
дельтаметод(~ exp(x1), b2, vb2)
## [1] 0,037
Пример 3: Относительный риск
В предыдущих двух примерах градиент было легко вычислить вручную, поскольку легко определить частные производные функции преобразования. Однако во многих случаях градиент трудно вычислить вручную, и в этих случаях функция deltamethod действительно может сэкономить нам некоторое время. Как и прежде, мы вычислим стандартные ошибки дельта-метода вручную, а затем покажем, как использовать
Как и прежде, мы вычислим стандартные ошибки дельта-метода вручную, а затем покажем, как использовать deltamethod , чтобы получить те же стандартные ошибки гораздо проще.
В этом примере мы хотели бы получить стандартную ошибку относительного риска, оцененного на основе логистической регрессии. Относительный риск – это отношение вероятностей. Мы будем работать с очень простой моделью, чтобы облегчить ручные вычисления. В этой модели мы прогнозируем вероятность зачисления в программу с отличием по результатам чтения. Мы хотели бы знать относительный риск попасть в программу с отличием, когда оценка по чтению составляет 50, по сравнению с тем, когда оценка по чтению составляет 40.
d <- read.csv("https://stats.idre.ucla.edu/stat/data/hsbdemo.csv")
d$honors <- factor(d$honors, level=c("не зачислен", "зачислен"))
m4 <- glm (почести ~ чтение, данные = d, семья = бином)
резюме (м4)
## ## Вызов: ## glm(formula = honors ~ read, family = binomial, data = d) ## ## Остаточное отклонение: ## Мин.1 кв. Медиана 3 кв. Макс. ## -1,966 -0,662 -0,404 0,671 2,092 ## ## Коэффициенты: ## Оценить стандарт. Значение ошибки z Pr(>|z|) ## (Перехват) -8,3002 1,2461 -6,66 2,7e-11 *** ## чтение 0,1326 0,0217 6,12 9.5е-10*** ## --- ## Значение. коды: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 '' 1 ## ## (Параметр дисперсии для биномиального семейства принимается равным 1) ## ## Нулевое отклонение: 231,29 на 199 степенях свободы ## Остаточное отклонение: 179,06 на 198 степенях свободы ## АИК: 183,1 ## ## Количество итераций оценки Фишера: 5
Давайте получим предсказанные вероятности наград, когда прочитано 50 и когда прочитано 40. Затем мы получим их отношение, относительный риск. Аргумент type="response" вернет прогнозируемое значение на шкале переменной ответа, здесь шкала вероятности.
p50 <- прогнозировать (m4, новые данные = данные. кадр (чтение = 50), тип = "ответ") р50
## 1 ## 0,158
p40 <- прогнозировать (m4, новые данные = данные.кадр (чтение = 40), тип = "ответ") р40
## 1 ## 0,0475
отн_риск <- p50/p40 rel_risk
## 1 ## 3.33
Учащиеся с 50 баллами по чтению имеют в 3,33 раза больше шансов быть зачисленными с отличием, чем те, у кого 40 баллов по чтению.
Теперь нам нужна стандартная ошибка этого относительного риска. Как всегда, для начала нам нужно определить преобразование относительного риска как функцию коэффициентов регрессии. Во-первых, мы должны определить условную вероятность с точки зрения коэффициентов регрессии. В нашей модели, учитывая оценку по чтению X, вероятность того, что учащийся будет зачислен в программу с отличием, составляет:
$$ Pr(Y = 1|X) = \frac{1}{1 + \exp(- \beta \cdot X)} $$
В нашем простом примере \(\beta = (b0, b1 )\). Следовательно, вероятность быть зачисленным в отличники при чтении = 50 равна \(Pr(Y = 1|X=50) = \frac{1}{1 + \exp(-b0 – b1 \cdot 50)}\), а при чтении = 40 вероятность быть зачисленным с отличием равна \(Pr(Y = 1|X=40) = \frac{1}{1 + \exp(-b0 – b1 \cdot 40)}\). Относительный риск — это просто отношение этих вероятностей. Итак, уравнение для функции относительного преобразования \(G(X)\) (с использованием общих X_1 и X_2 вместо 50 и 40 соответственно):
Относительный риск — это просто отношение этих вероятностей. Итак, уравнение для функции относительного преобразования \(G(X)\) (с использованием общих X_1 и X_2 вместо 50 и 40 соответственно):
$$ G(X) = \frac{\frac{1}{1 + \exp(-b_0 – b_1 \cdot X_1)}}{\frac{1}{1 + \exp(-b_0 – b_1 \ cdot X_2)}}, $$
, что упрощается до:
$$ G(X) = \frac{1 + \exp(-b_0 – b_1 \cdot X_2)}{1 + \exp(-b_0 – b_1 \cdot X_1)}. $$
Теперь нам нужен градиент, \(\nabla G(X)\). Используя правило произведения и цепное правило, мы получаем следующие частные производные:
$$ \frac{dG}{db_0} = -\exp(-b_0 – b_1 \cdot X_2) \cdot p1 + (1 + \exp( -b_0 – b_1 \cdot X_2)) \cdot p1 * (1 – p1) $$
и
$$ \frac{dG}{db_1} = -\exp(-b_0 – b_1 \cdot X_2) \cdot X_2 \cdot p1 + (1 + \exp(-b_0 – b_1 \cdot X_2)) \cdot X_1 \cdot p1 * (1 – p1), $$
, где \(p1 = Pr(Y = 1|X1) = \frac{1}{1 + \exp(-b0 – b1 \cdot X_1) }\), поэтому в нашем случае вероятность зачисления при чтении = 50. Рассчитаем наш градиент:
x1 <- 50 х2 <- 40 b0 <- коэфф(m4)[1] b1 <- коэфф(m4)[2] e1 <- ехр(-b0 - 50*b1) e2 <- ехр(-b0 - 40*b1) р1 <- 1/(1+е1) р2 <- 1/(1+е2) dgdb0 <- -e2*p1 + (1+e2)*p1*(1-p1) dgdb1 <- -x2*e2*p1 + (1+e2)*x1*p1*(1-p1) град <- с(dgdb0, dgdb1) выпускник
## (Перехват) (Перехват) ## -0,368 13,280
Теперь мы можем рассчитать стандартную ошибку, как и раньше.
vG <- t(град) %*% vcov(м4) %*% (град) кврт(ВГ)
## [1] ## [1,] 0,745
При расчете более сложного градиента дельта-метод действительно может сэкономить нам время. К счастью, \(G(X)\) не так уж плохо указать.
дельтаметод( ~ (1 + exp(-x1 - 40*x2))/(1 + exp(-x1 - 50*x2)), c(b0, b1), vcov(m4))
## [1] 0,745
Гораздо проще!
Таким образом, R предоставляет удобную функцию для аппроксимации стандартных ошибок преобразований коэффициентов регрессии функцией deltamethod . Все, что необходимо, — это выражение преобразования и ковариация параметров регрессии.
4.1 Векторы смещения и скорости
Цели обучения
К концу этого раздела вы сможете:
- Вычислить векторы положения в многомерной задаче смещения.
- Решите для смещения в двух или трех измерениях.
- Рассчитать вектор скорости по заданному вектору положения как функцию времени.

- Вычислить среднюю скорость в нескольких измерениях.
Перемещение и скорость в двух или трех измерениях являются прямым расширением одномерных определений. Однако теперь они являются векторными величинами, поэтому вычисления с ними должны следовать правилам векторной алгебры, а не скалярной алгебры.
Вектор смещения
Чтобы описать движение в двух и трех измерениях, мы должны сначала установить систему координат и соглашение для осей. Обычно мы используем координаты x , y и z , чтобы определить местонахождение частицы в точке P ( x , y , z ) в трех измерениях. Если частица движется, переменные x , y и z являются функциями времени ( t ):
[латекс] x=x(t)\quad y=y(t)\quad z=z(t). [/latex]
Вектор положения от начала системы координат до точки P равен [латекс] \overset{\to}{r}(t). [/latex] В обозначении единичного вектора, введенном в системе координат и компонентах вектора, [latex] \overset{\to }{r}(t) [/latex] равен
[latex] \overset{\to} {r}(t)=x(t)\шляпа{i}+y(t)\шляпа{j}+z(t)\шляпа{k}. [/latex]
[/latex]
(рисунок) показывает систему координат и вектор к точке P , где частица может находиться в определенное время t . Обратите внимание на ориентацию осей x , y и z . Эта ориентация называется правой системой координат (Системы координат и компоненты вектора) и используется на протяжении всей главы.
Рис. 4.2 Трехмерная система координат с частицей в положении P(x(t), y(t), z(t)).
С нашим определением положения частицы в трехмерном пространстве мы можем сформулировать трехмерное смещение. (Рисунок) показывает частицу в момент времени [латекс] {t}_{1} [/латекс], расположенную в [латекс] {P}_{1} [/латекс] с вектором положения [латекс] \overset{\to } {г}({т}_{1}). [/latex] В более позднее время [latex] {t}_{2}, [/latex] частица находится в [latex] {P}_{2} [/latex] с вектором положения [latex] \overset {\ to} {r} ({t} _ {2}) [/ латекс]. вектор смещения [латекс] \text{Δ}\overset{\to }{r} [/latex] находится путем вычитания [латекс] \overset{\to }{r}({t}_{1}) [/латекс] из [латекс] \overset{\to }{r}({t}_{2})\text{ }: [/latex]
[латекс] \text{Δ}\overset{\to {r} = \ overset {\ to {r} ({t} _ {2}) - \ overset {\ to {r} ({t} _ {1}). [/latex]
[/latex]
Добавление вектора обсуждается в разделе Векторы. Обратите внимание, что это та же самая операция, которую мы проделали в одном измерении, но теперь векторы находятся в трехмерном пространстве.
Рисунок 4.3 Смещение [латекс] \text{Δ}\overset{\to }{r}=\overset{\to }{r}({t}_{2})-\overset{\to }{r}( {t}_{1}) [/latex] — это вектор из [latex] {P}_{1} [/latex] в [latex] {P}_{2} [/latex].
Следующие примеры иллюстрируют концепцию смещения в нескольких измерениях.
Пример
Полярно-орбитальный спутник
Спутник находится на круговой полярной орбите вокруг Земли на высоте 400 км, т. е. проходит прямо над головой на Северном и Южном полюсах. Каковы величина и направление вектора смещения от момента, когда он находится прямо над Северным полюсом, до момента, когда он находится на широте [latex] -45\text{°} [/latex]?
Стратегия
Мы создаем картину проблемы, чтобы визуализировать решение графически. Это поможет нам понять смещение. Затем мы используем единичные векторы для решения смещения.
Затем мы используем единичные векторы для решения смещения.
Решение
Показать ответ
В представлении единичного вектора векторы положения равны
[латекс] \begin{array}{cc} \overset{\to }{r}({t}_{1})=6770.\,\text{ км}\шляпа{j}\hfill\\\overset{\to }{r}({t}_{2})=6770.\,\text{км}\,(\text{cos}\,45 \text{°})\шляпа{i}+6770.\,\text{км}\,(\text{sin}(-45\text{°}))\шляпа{j}.\end{массив} [/латекс]
Вычисляя синус и косинус, мы имеем
[латекс] \begin{array}{cc} \hfill \overset{\to }{r}({t}_{1})& =\hfill & 6770. \шляпа{j}\hfill \\ \hfill \overset{\to }{r}({t}_{2})& =\hfill & 4787\шляпа{i}-4787\шляпа{j}.\hfill \end{array} [/latex]
Теперь мы можем найти [latex] \text{Δ}\overset{\to }{r} [/latex], смещение спутника:
[latex] \text {Δ} \ overset {\ to {r} = \ overset {\ to {r} ({t} _ {2}) - \ overset {\ to {r} ({t} _ {1}) = 4787 \ шляпа {i} - 11 557 \ шляпа {j}. [/латекс] 9{-1}(\frac{-11 557}{4787})=-67,5\text{°}. [/latex]
[/latex]
Значимость
Построение графика смещения дает информацию и значение для решения задачи в виде единичного вектора. При построении графика смещения нам необходимо включить его компоненты, а также его величину и угол, который он образует с выбранной осью — в данном случае с осью x ((Рисунок)).
Рисунок 4.5 Вектор смещения с компонентами, углом и величиной.
Обратите внимание, что в этом примере спутник прошел криволинейный путь вдоль своей круговой орбиты, чтобы добраться из начального положения в конечное. Он также мог пройти 4787 км на восток, затем 11 557 км на юг, чтобы достичь того же места. Оба этих пути длиннее, чем длина вектора смещения. Фактически вектор смещения задает кратчайший путь между двумя точками в одном, двух или трех измерениях.
Многие приложения в физике могут иметь серию перемещений, как обсуждалось в предыдущей главе. Общее смещение — это сумма индивидуальных смещений, только на этот раз нам нужно быть осторожными, потому что мы добавляем векторы. Проиллюстрируем это понятие на примере броуновского движения.
Проиллюстрируем это понятие на примере броуновского движения.
Пример
Броуновское движение
Броуновское движение — хаотическое беспорядочное движение взвешенных в жидкости частиц, возникающее в результате столкновений с молекулами жидкости. Это движение трехмерно. Смещения в числовом порядке частицы, совершающей броуновское движение, могут выглядеть следующим образом в микрометрах ((рисунок)):
[латекс] \begin{array}{cc} \hfill \text{Δ}{\overset{\to }{r}}_{1}& =\hfill & 2.0\шляпа{i}+\шляпа{ j} +3,0 \ шляпа {k} \ hfill \\ \ hfill \ text {Δ} {\ overset {\ to {r}} _ {2} & = \ hfill & \ text {−} \ hat {i} +3,0 \ шляпа {k} \ hfill \\ \ hfill \ text {Δ} {\ overset {\ to {r}} _ {3} & = \ hfill & 4,0 \ hat {i} -2,0 \ hat {j }+\шляпа{k}\hfill \\ \hfill \text{Δ}{\overset{\to}}{r}}_{4}& =\hfill & -3.0\шляпа{i}+\шляпа{j }+2.0\hat{k}.\hfill \end{array} [/latex]
Каково полное смещение частицы от начала координат?
Рис. 4.6 Траектория частицы, совершающей случайные смещения броуновского движения. Общее смещение показано красным.
4.6 Траектория частицы, совершающей случайные смещения броуновского движения. Общее смещение показано красным.
Решение
Показать ответ
Значимость
Из рисунка видно, что величина полного смещения меньше суммы величин отдельных перемещений.
Вектор скорости
В предыдущей главе мы нашли мгновенную скорость, вычислив производную функции положения по времени. Мы можем сделать ту же операцию в двух и трех измерениях, но мы используем векторы. Мгновенное вектор скорости теперь равен
[латекс] \ overset {\ to {v} (t) = \ underset {\ text {Δ} t \ to 0} {\ text {lim}} \ frac {\ overset { \ to {r} (t + \ text {Δ} t) - \ overset {\ to {r} (t)} {\ text {Δ} t} = \ frac {d \ overset {\ to} {r }}{дт}. [/latex]
Давайте посмотрим на относительную ориентацию вектора положения и вектора скорости графически. На (рис.) показаны векторы [латекс] \overset{\to }{r}(t) [/latex] и [латекс] \overset{\to }{r}(t+\text{Δ}t), [/latex], которые дают положение частицы, движущейся по пути, представленному серой линией. Когда [latex] \text{Δ}t [/latex] стремится к нулю, вектор скорости, заданный (рис.), становится касательным к пути частицы в момент времени т .
Когда [latex] \text{Δ}t [/latex] стремится к нулю, вектор скорости, заданный (рис.), становится касательным к пути частицы в момент времени т .
Рис. 4.7 Частица движется по пути, указанному серой линией. В пределе, когда [latex] \text{Δ}t [/latex] стремится к нулю, вектор скорости становится касательным к пути частицы.
(уравнение) также можно записать в терминах компонентов [латекс] \overset{\to }{v}(t). [/латекс] Так как
[латекс] \overset{\to}}{r}(t)=x(t)\шляпа{i}+y(t)\шляпа{j}+z(t)\шляпа{ k}, [/latex]
мы можем написать
[латекс] \overset{\to }{v}(t)={v}_{x}(t)\hat{i}+{v}_ {y}(t)\шляпа{j}+{v}_{z}(t)\шляпа{k} [/латекс]
, где
[латекс] {v}_{x}(t)=\frac{dx(t)}{dt},\quad {v}_{y}(t)=\frac{dy(t) )}{dt},\quad {v}_{z}(t)=\frac{dz(t)}{dt}. [/latex]
Если интересует только средняя скорость, то у нас есть векторный эквивалент одномерной средней скорости для двух и трех измерений:
[латекс] {\overset{\to} {v}}_ {\ text {среднее}} = \ frac {\ overset {\ to {r} ({t} _ {2}) - \ overset {\ to {r} ({t} _ {1})} { {т}_{2}-{т}_{1}}. [/latex]
[/latex]
Пример
Расчет вектора скорости 9{2}\шляпа{i}+(2,0+3,0t)\шляпа{j}+5,0t\шляпа{k}\текст{m}. [/latex] (а) Чему равны мгновенная скорость и скорость при
t = 2,0 с? б) Какова средняя скорость между 1,0 и 3,0 с?Решение
Используя (Рисунок) и (Рисунок) и взяв производную функции положения по времени, находим
Показать ответ
(b) От (Рисунок),
Показать ответ
Значение
Мы видим, что средняя скорость такая же, как мгновенная скорость в 9{3}\шляпа{i}+4.0\шляпа{j}. [/latex] (а) Чему равна мгновенная скорость t = 3 с? (b) Равна ли средняя скорость между 2 и 4 с мгновенной скорости в t = 3 с?
Показать раствор
Независимость перпендикулярных движений
Когда мы смотрим на трехмерные уравнения для положения и скорости, записанные в виде единичного вектора, (Рисунок) и (Рисунок), мы видим, что компоненты этих уравнений являются отдельными и уникальными функциями времени которые не зависят друг от друга. Движение по 9Направление 0024 x не имеет части своего движения по направлениям y и z , и аналогично для двух других осей координат. Таким образом, движение объекта в двух или трех измерениях можно разделить на отдельные независимые движения вдоль перпендикулярных осей той системы координат, в которой происходит движение.
Движение по 9Направление 0024 x не имеет части своего движения по направлениям y и z , и аналогично для двух других осей координат. Таким образом, движение объекта в двух или трех измерениях можно разделить на отдельные независимые движения вдоль перпендикулярных осей той системы координат, в которой происходит движение.
Чтобы проиллюстрировать эту концепцию в отношении перемещения, рассмотрим женщину, идущую из точки A в точку B в городе с квадратными кварталами. Женщина, идущая по пути из A - B может пройти столько-то блоков на восток, а затем на север (два перпендикулярных направления) еще один набор блоков, чтобы добраться до B . Насколько далеко она пойдет на восток, зависит только от ее движения на восток. Точно так же на то, как далеко она пойдет на север, влияет только ее движение на север.
Независимость движения
В кинематическом описании движения мы можем рассматривать горизонтальную и вертикальную составляющие движения отдельно. Во многих случаях движение в горизонтальном направлении не влияет на движение в вертикальном направлении, и наоборот.
Во многих случаях движение в горизонтальном направлении не влияет на движение в вертикальном направлении, и наоборот.
Примером, иллюстрирующим независимость вертикального и горизонтального движений, являются два бейсбольных мяча. Один бейсбольный мяч выпадает из состояния покоя. В тот же момент с той же высоты горизонтально брошен другой снаряд, летящий по криволинейной траектории. Стробоскоп фиксирует положение шаров через фиксированные промежутки времени по мере их падения ((Рисунок)).
Рис. 4.8 Схема движения двух одинаковых шаров: один падает из состояния покоя, а другой имеет начальную горизонтальную скорость. Каждая последующая позиция представляет собой равный интервал времени. Стрелки представляют горизонтальную и вертикальную скорости в каждой позиции. Мяч справа имеет начальную горизонтальную скорость, тогда как мяч слева не имеет горизонтальной скорости. Несмотря на разницу в горизонтальных скоростях, вертикальные скорости и положения обоих шаров одинаковы, что показывает, что вертикальное и горизонтальное движения независимы.
Примечательно, что при каждой вспышке стробоскопа вертикальное положение двух шаров одинаково. Это сходство подразумевает, что вертикальное движение не зависит от того, движется ли мяч горизонтально. (Если предположить отсутствие сопротивления воздуха, вертикальное движение падающего объекта зависит только от силы тяжести, а не от каких-либо горизонтальных сил.) Тщательное изучение мяча, брошенного горизонтально, показывает, что он проходит такое же расстояние по горизонтали между вспышками. Это связано с тем, что после броска на мяч в горизонтальном направлении не действуют дополнительные силы. Этот результат означает, что горизонтальная скорость постоянна и не зависит ни от вертикального движения, ни от гравитации (которая является вертикальной). Обратите внимание, что этот случай верен только для идеальных условий. В реальном мире сопротивление воздуха влияет на скорость мячей в обоих направлениях.
Двумерная кривая траектория горизонтально брошенного мяча состоит из двух независимых одномерных движений (горизонтального и вертикального). Ключом к анализу такого движения, называемого движением снаряда , является разложение его на движения в перпендикулярных направлениях. Разложение двумерного движения на перпендикулярные компоненты возможно, поскольку компоненты независимы.
Ключом к анализу такого движения, называемого движением снаряда , является разложение его на движения в перпендикулярных направлениях. Разложение двумерного движения на перпендикулярные компоненты возможно, поскольку компоненты независимы.
Резюме
- Функция положения [латекс] \overset{\to }{r}(t) [/латекс] дает положение как функцию времени частицы, движущейся в двух или трех измерениях. Графически это вектор от начала выбранной системы координат до точки, в которой находится частица в определенное время.
- Вектор смещения [латекс] \text{Δ}\overset{\to }{r} [/латекс] дает кратчайшее расстояние между любыми двумя точками на траектории частицы в двух или трех измерениях.
- Мгновенная скорость дает скорость и направление движения частицы в определенный момент времени на ее траектории в двух или трех измерениях и представляет собой вектор в двух и трех измерениях.
- Вектор скорости касается траектории частицы.
- Перемещение [латекс] \overset{\to }{r}(t) [/latex] можно представить в виде векторной суммы одномерных перемещений [латекс] \overset{\to }{x}(t), \overset{\to}{y}(t),\overset{\to}{z}(t) [/latex] вдоль x , y и z направлений.

- Скорость [латекс] \overset{\to }{v}(t) [/латекс] может быть записана как векторная сумма одномерных скоростей [латекс] {v}_{x}(t),{v }_{y}(t),{v}_{z}(t) [/latex] вдоль направлений x , y и z .
- Движение в любом заданном направлении не зависит от движения в перпендикулярном направлении.
Концептуальные вопросы
Какую форму имеет траектория частицы, если расстояние от любой точки A до точки B равно величине смещения от A до B ?
Показать раствор
Приведите пример траектории в двух или трех измерениях, вызванной независимыми перпендикулярными движениями.
Если мгновенная скорость равна нулю, что можно сказать о наклоне функции положения?
Показать раствор
Задачи
Координаты частицы в прямоугольной системе координат (1.0, –4.0, 6.0). Каков вектор положения частицы?
Показать решение
Положение частицы меняется с [латекс] {\overset{\to }{r}}_{1}=(2. 0\text{}\шляпа{i}+3.0\шляпа{j})\текст {см} [/ латекс] до [латекс] {\ overset {\ to} {r}} _ {2} = (-4,0 \ шляпа {i} + 3,0 \ шляпа {j}) \, \ текст {см} . [/latex] Каково смещение частицы?
0\text{}\шляпа{i}+3.0\шляпа{j})\текст {см} [/ латекс] до [латекс] {\ overset {\ to} {r}} _ {2} = (-4,0 \ шляпа {i} + 3,0 \ шляпа {j}) \, \ текст {см} . [/latex] Каково смещение частицы?
18-я лунка на поле для гольфа Pebble Beach представляет собой изгиб влево длиной 496,0 м. Фарватер от ти принимается за направление x . Игрок в гольф наносит удар с ти с расстояния 300,0 м, что соответствует смещению [латекс] \text{Δ}{\overset{\to }{r}}_{1}=300,0\,\text{m}\hat {i}, [/latex] и наносит второй удар 189.0 м при водоизмещении [латекс] \text{Δ}{\overset{\to }{r}}_{2}=172,0\,\text{м}\шляпа{i}+80,3\,\text{ м}\шляпа{j}. [/latex] Каково окончательное смещение мяча для гольфа с площадки-ти?
Показать раствор
Птица летит прямо на северо-восток на расстояние 95,0 км за 3,0 часа. С осью x строго на восток и осью y строго на север, каково смещение в представлении единичного вектора для птицы? Какова средняя скорость в пути?
Велосипедист проезжает 5,0 км строго на восток, затем 10,0 км [латекс] 20\text{°} [/латекс] западнее севера. {3}\шляпа{к}\текст{м}. [/latex] (a) Какова скорость частицы в 0 с и в [latex] 1,0 [/latex] с? (b) Какова средняя скорость между 0 с и [латекс] 1,0 [/латекс] с?
{3}\шляпа{к}\текст{м}. [/latex] (a) Какова скорость частицы в 0 с и в [latex] 1,0 [/latex] с? (b) Какова средняя скорость между 0 с и [латекс] 1,0 [/латекс] с?
Показать решение
Клэй Мэтьюз, полузащитник команды Green Bay Packers, может развивать скорость до 10,0 м/с. В начале игры Мэтьюз бежит по полю на [латекс] 45\текст{°} [/латекс] относительно 50-ярдовой линии и преодолевает 8,0 м за 1 с. Затем он бежит прямо по полю со скоростью [latex] 90\text{°} [/latex] относительно 50-ярдовой линии на протяжении 12 м с истекшим временем 1,2 с. а) Каково окончательное перемещение Мэтьюза с начала пьесы? б) Какова его средняя скорость?
F-35B Lighting II — реактивный истребитель с укороченным взлетом и вертикальной посадкой. Если он совершает вертикальный взлет до высоты 20,00 м над землей, а затем следует по траектории полета под углом [latex] 30\text{°} [/latex] по отношению к земле на протяжении 20,00 км, каково конечное перемещение?
Показать раствор
Глоссарий
- вектор смещения
- вектор из начального положения в конечное положение на траектории частицы
- вектор положения
- вектор от начала выбранной системы координат до положения частицы в двух- или трехмерном пространстве
- вектор скорости
- вектор, задающий мгновенную скорость и направление движения частицы; касательной к траектории
Что такое дельта-метод?
Что такое дельта-метод?Алекс Голд, Нат Олин, Энни Ван
21.
 {-1} (X \beta))}{d(X \beta)}\) для сокращения времени вычислений по сравнению с методами моделирования или начальной загрузки.
{-1} (X \beta))}{d(X \beta)}\) для сокращения времени вычислений по сравнению с методами моделирования или начальной загрузки.Дельта-метод — это общий метод получения дисперсии функции асимптотически нормальных случайных величин с известной дисперсией. В этом случае дельта-метод использует тот факт, что маржа (обычно) является бесконечно дифференцируемой функцией данных, \(X\) и вектора \(\бета\) s для получения замкнутой формы Решение для стандартных ошибок поля. 1
В частности, дельта-метод использует разложение в ряд Тейлора функции обратной связи регрессии для аппроксимации поля в окрестности \(X\) и \(\бета\)s и получения вариации вблизи эта точка. 9{-1}(X_1 \beta))}{d(X \beta)}\]
В зависимости от того, действует ли эффект на непрерывную или категориальную переменную, это может быть фактическая производная (мгновенная скорость изменения) или вычитание \(P(X\beta)\), вычисленное при одном значении \(X\), из другого (первое отличие).
Используя разложение Тейлора, мы можем аппроксимировать \(P\), произвольную функцию случайной величины \(X \beta\) вокруг точки \(X_1 \beta\), как 3
\[P (X\beta) = P(X_1\beta) + \frac{d(P(X_1\beta))}{d(X\beta)}(X\beta - X_1\beta)\] 9{-1}(X_1\бета))}{d(X\бета)}\право) \end{выровнено} \]
Приведенные выше уравнения описывают, как аппроксимировать предсказанные уровни или эффекты, но почему бы просто не рассчитать нашу оценку \(P(X\beta)\) напрямую?
Что ж, мы можем сделать это для точечной оценки, но также хотим вычислить ошибки этой оценки, а дисперсия \(P(X\beta)\) неизвестна. К счастью, мы можем вычислить дисперсию приведенных выше приближений. Википедия содержит действительно хороший вывод многомерного дельта-метода:
К счастью, мы можем вычислить дисперсию приведенных выше приближений. Википедия содержит действительно хороший вывод многомерного дельта-метода:
\[\text{Var}[P(X \beta)] = \text{Var}\left[P(X_1 \beta) + \frac{d(P(X_1 \beta))}{d(X \beta)}(X\beta - X_1 \beta)\right]\]
Поскольку \(X_1\beta\) является известной точкой, ее дисперсия равна нулю, поэтому это упрощается до
\[\text{ Var}[P(X\beta)] = \text{Var}\left[\frac{d(P(X_1\beta))}{d(X\beta)} \cdot X\beta\right]\]
Первый член дисперсии — это вектор частных производных нашей оценки, также известный как наша матрица Якоби. 4 Для любого прогнозируемого уровня, индексированного \(i\) в регрессии, \(i,j\)-й элемент якобиана будет производной прогнозируемого уровня \(i\) по отношению к регрессору \(j \). Это фиксированные количества. Мы также знаем дисперсию \(X\beta\), так как это наша матрица дисперсии-ковариации \(V\). 9T \ V \left(\frac{d(P(X_1 \beta))}{d(X\beta)}\right)\]
Итак, практически говоря, чтобы получить нашу дисперсию, мы предварительно и опубликуем - умножить частные производные функции обратной связи на исходную дисперсионно-ковариационную матрицу из регрессии.
Короче говоря,
Вычислите матрицу Якоби функции обратной связи \(X \beta\), \(J\). 7
Получите матрицу дисперсии-ковариации \(V\) из выходных данных регрессии или рассчитайте ее другим способом. 9{Т} V J\). В итоге вы получите матрицу \(k \times 1\) для \(k\) предсказанных уровней/эффектов.
Допустим, мы подгоняем логистическую регрессию, используя данные margex , и нас интересует прогнозируемый результат для различных групп лечения:
библиотека (modmarg) данные(margex) lg <- glm(результат ~ лечение * возраст, данные = margex, семья = 'биномиальный') резюме (lg)
## ## Вызов: ## glm(formula = результат ~ лечение * возраст, семья = "биномиальный", ## данные = margex) ## ## Остаточное отклонение: ## Мин. 1 кв. Медиана 3 кв. Макс. ## -1,3200 -0,6033 -0,3212 -0,1580 2,9628 ## ## Коэффициенты: ## Оценить стандарт. Значение ошибки z Pr(>|z|) ## (Перехват) -7,03092 0,50247 -13,993 <2e-16 *** ## лечение 1,35170 0,62208 2,173 0,0298 * ## возраст 0,11060 0,01069 10,347 <2e-16 *** ## лечение:возраст -0,01046 0,01301 -0,804 0,4216 ## --- ## Значение.коды: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 '' 1 ## ## (Параметр дисперсии для биномиального семейства принимается равным 1) ## ## Нулевое отклонение: 2732.1 на 2999 степеней свободы ## Остаточное отклонение: 2169,4 на 2996 степеней свободы ## АИК: 2177,4 ## ## Количество итераций оценки Фишера: 6
, где обработка переменная \(\tau \in {0, 1}\). Каков средний результат, когда \(\tau = 0\) или \(\tau = 1\)?
Основываясь только на этих результатах, мы на самом деле не знаем, каков будет прогнозируемый результат для разных групп лечения, потому что мы не можем напрямую интерпретировать коэффициенты: есть член взаимодействия, и эффект каждой ковариаты зависит от уровней другие ковариаты.
Точечные оценки
Чтобы получить оценку средних уровней результата для различных значений лечения, мы можем установить лечение на 0 или 1 для всего набора данных, сгенерировать прогнозируемые результаты для набора данных и усреднить результаты (в других словами, каким был бы результат, если бы все были в контрольной/лечебной группе?). n \frac{1}{1 + \exp(-X_i\beta)}
\] Теперь давайте сделаем это в R: установим обработку на 0 или 1, сгенерируем линейные предикторы, преобразуем их в прогнозируемые результаты и возьмем среднее значение.
n \frac{1}{1 + \exp(-X_i\beta)}
\] Теперь давайте сделаем это в R: установим обработку на 0 или 1, сгенерируем линейные предикторы, преобразуем их в прогнозируемые результаты и возьмем среднее значение.
# Извлечь nxk матрицу данных х <- model.matrix(lg) # Извлечь коэффициенты из модели (вектор-столбец с k элементами) бета <- матрица (коэффициенты lg $) # КОНТРОЛЬ: # Установить для лечения и лечения:возраст значение 0 для всех наблюдений х[ "лечение"] <- 0 x[ 'лечение:возраст'] <- x[ 'лечение'] * x[ 'возраст'] # Получить линейные предикторы pred_ctl <- x %*% бета # Примените функцию обратной ссылки, чтобы получить предсказанные вероятности pp_ctl <- 1 / (1 + exp(-pred_ctl)) # Получить среднюю прогнозируемую вероятность mean_pp_ctl <- среднее (pp_ctl) # ЛЕЧЕНИЕ: # Установите обработку на 1 и обработку: от возраста к возрасту для всех наблюдений х[ "лечение"] <- 1 x[ 'лечение:возраст'] <- x[ 'лечение'] * x[ 'возраст'] # Получить линейные предикторы pred_treat <- x %*% бета # Примените функцию обратной ссылки, чтобы получить предсказанные вероятности pp_treat <- 1 / (1 + exp(-pred_treat)) # Получить среднюю прогнозируемую вероятность mean_pp_treat <- означает (pp_treat) # ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ: среднее_pp_ctl
## [1] 0,1126685
mean_pp_treat
## [1] 0,208375
Дисперсия
Пока это довольно просто, но мы хотим знать стандартную ошибку этих оценок.
У вас может возникнуть соблазн просто использовать команду R, прогнозировать(модель, новые данные, se.fit = TRUE) , исправить обработку на 0 или 1 и найти среднее значение полученных стандартных ошибок. Не делай этого! Вы усредните стандартные ошибки прогнозируемого результата каждого наблюдения в вашем наборе данных, что составляет 92}
\конец{массив}
\Правильно]
\оставил[
\начать{массив}{cccc}\\
1 & \tau_1 & \text{age}_1 & \tau_1 \cdot \text{age}_1 \\
1 & \tau_2 & \text{age}_2 & \tau_2 \cdot \text{age}_2 \\
\vdots & \vdots & \vdots & \vdots\\
1 & \tau_n & \text{age}_n & \tau_n \cdot \text{age}_n \\
\конец{массив}
\Правильно]
\]
Первое слагаемое применяет производную функции обратной связи ко всем линейным предикторам в модели, а второе слагаемое представляет собой ковариатную матрицу из наших данных! Как удобно! Это будет верно для всех общих линейных моделей. Таким образом, мы можем переписать это как 92)
# Установить лечение на 0
х[ 'лечение'] <- 0
x[ 'лечение:возраст'] <- x[ 'лечение'] * x[ 'возраст']
# Завершите цепное правило путем матричного умножения производных на данные,
# теперь у нас есть якобиан
j <- производная %*% x/nrow(x)
# Дисперсия нашей оценки является перекрестным произведением якобиана и модели
# ковариационно-дисперсионная матрица
дисперсия <- j %*% vcov(lg) %*% t(j)
# Ошибка равна квадратному корню из этого
se_ctl <- sqrt (diag (дисперсия))
# ОШИБКА ОБРАЩЕНИЯ: та же логика
deriv <- as. 2)
х <- model.matrix(lg)
х[ 'лечение'] <- 1
x[ 'лечение:возраст'] <- x[ 'лечение'] * x[ 'возраст']
j <- производная %*% x/nrow(x)
дисперсия <- j %*% vcov(lg) %*% t(j)
se_treat <- sqrt (diag (дисперсия))
se_ctl
2)
х <- model.matrix(lg)
х[ 'лечение'] <- 1
x[ 'лечение:возраст'] <- x[ 'лечение'] * x[ 'возраст']
j <- производная %*% x/nrow(x)
дисперсия <- j %*% vcov(lg) %*% t(j)
se_treat <- sqrt (diag (дисперсия))
se_ctl
## [1] 0.009334252
se_treat
## [1] 0.0067
Обзор
Хорошо, у нас есть наши оценки и дисперсия:
результат <- data
Метка = c("лечение = 0", "лечение = 1"),
Маржа = c(mean_pp_ctl, mean_pp_treat),
Standard.Error = c(se_ctl, se_treat)
)
результат ## Label Margin Standard.Error ## 1 лечение = 0 0,1126685 0,009334252 ## 2 обработка = 1 0.2083750 0.0067
Что мы получаем от modmarg?
marg <- modmarg::marg(mod = lg, var_interest = 'лечение')
marg[[1]][ c("Ярлык", "Поля", "Стандарт.Ошибка")] ## Поля Метки Стандарт.Ошибка ## 1 лечение = 0 0,1126685 0,009334252 ## 2 обработка = 1 0.2083750 0.0067
Ура!
«Обычно», потому что это утверждение требует, чтобы каноническая функция связи для регрессии имела производную в закрытой форме.
 К счастью, это верно для большинства распространенных форм линейной регрессии.↩︎
К счастью, это верно для большинства распространенных форм линейной регрессии.↩︎Точная форма функции связи и ее инверсии будет зависеть от типа регрессии. Например, логит-функция является канонической функцией связи для логистической регрессии и позволяет выполнять преобразования между вероятностями и логарифмическими шансами.↩︎
Обратите внимание, что входные данные \(X\) рассматриваются как фиксированные, а \(\beta\) - как случайная величина.↩︎
Матрица Якоби — это просто название матрицы всех первых частных производных вектор-функции.↩︎ 9Т\).↩︎
Несколько практических замечаний по вычислению якобиана: пример в нижней части виньетки довольно точно показывает, как вычислить якобиан для предсказанных уровней. Для прогностических эффектов большое изменение заключается в том, что теперь вы вычисляете дисперсию прогнозируемых эффектов, поэтому вам нужно взять вторую производную функции связи (вместо первой производной).
 Для категориальных переменных вы можете взять вторую производную, вычитая каждый из уровней из базового уровня и возвращая это как якобиан. Для непрерывных переменных вам необходимо фактически вычислить вторую производную функции связи и использовать ее вместо первой производной выше. Вам нужно явно вычислить вторую производную, потому что вам нужна мгновенная скорость изменения, а не скорость изменения в диапазоне, как в случае с категориальными переменными выше.↩︎ 9{-1}(-X\бета)\)↩︎
Для категориальных переменных вы можете взять вторую производную, вычитая каждый из уровней из базового уровня и возвращая это как якобиан. Для непрерывных переменных вам необходимо фактически вычислить вторую производную функции связи и использовать ее вместо первой производной выше. Вам нужно явно вычислить вторую производную, потому что вам нужна мгновенная скорость изменения, а не скорость изменения в диапазоне, как в случае с категориальными переменными выше.↩︎ 9{-1}(-X\бета)\)↩︎
Как выполнить метод Delta-Delta Ct
Что такое метод Delta-Delta Ct?
Метод дельта-дельта Ct, также известный как метод 2 – ∆∆Ct , представляет собой простую формулу, используемую для расчета относительной кратности экспрессии генов образцов при выполнении полимеразной цепной реакции в реальном времени (также известный как кПЦР). Этот метод был разработан Кеннетом Ливаком и Томасом Шмитгеном в 2001 году и цитировался более 61 000 раз.
Mastering qPCR
Дополнительные видеоуроки по анализу данных qPCR можно найти в нашем курсе Mastering qPCR
>>Используйте код 20QPCR , чтобы получить 20% скидка <<
БЕСПЛАТНЫЙ шаблон Microsoft Excel
4 90 БЕСПЛАТНЫЙ шаблон Excel, который содержит все формулы, описанные в этой статье ниже. Используйте это, чтобы попрактиковаться и освоить расчеты. Все сделано за вас, все, что требуется, это значения Ct!Если вы хотите загрузить это, просто нажмите здесь.
Понимание формулы метода дельта-дельта Ct
Прежде чем приступать непосредственно к расчетам, стоит понять, что означает формула дельта-дельта Ct.
Общая формула для расчета уровня экспрессии гена относительной укладки может быть представлена как:
Это выглядит как страшная математическая формула, хотя на самом деле это не так. Давайте разобьем формулу на более понятные части.
Во-первых, Ct обозначает порог цикла (Ct) вашего образца. Это дается после реакции qPCR машиной qPCR. Проще говоря, это номер цикла, при котором флуоресценция, генерируемая ПЦР, отличается от фонового шума.
Это дается после реакции qPCR машиной qPCR. Проще говоря, это номер цикла, при котором флуоресценция, генерируемая ПЦР, отличается от фонового шума.
Символ ∆ относится к треугольнику. Дельта — это математический термин, используемый для описания разницы между двумя числами. Так что полезно использовать при обобщении длинных формул.
Итак, давайте посмотрим, что ∆∆Ct часть уравнения означает:
∆∆Ct = ∆Ct (обработанный образец) – ∆Ct (необработанный образец) значения обработанного/экспериментального образца и необработанного/контрольного образца. Но к чему относится ∆Ct ?
Давайте посмотрим:
∆Ct = Ct (интересующий ген) – Ct (ген домашнего хозяйства) заданный образец. Это делается для того, чтобы нормализовать интересующий ген к гену, на который не влияет ваш эксперимент, отсюда и термин «ген-домашнее хозяйство».
Использование формулы дельта-дельта Ct для расчета экспрессии гена
Чтобы использовать метод дельта-дельта Ct, вам потребуются значения Ct для интересующего гена и гена домашнего хозяйства как для обработанных, так и для необработанных образцов. Если у вас более одного гена домашнего хозяйства, возможно, стоит ознакомиться с руководством по анализу данных количественной ПЦР с многочисленными эталонными генами.
Если у вас более одного гена домашнего хозяйства, возможно, стоит ознакомиться с руководством по анализу данных количественной ПЦР с многочисленными эталонными генами.
Вот как рассчитать относительную экспрессию генов за 5 простых шагов.
1. Усреднение значений Ct для любых технических повторностей
Первым шагом является усреднение значений Ct для технических повторов каждого образца. Таким образом, например, при выполнении количественной ПЦР в двух или трех повторностях эти значения необходимо сначала усреднить. В приведенном ниже примере каждый образец был запущен в двух экземплярах ( Ct1 и Ct2 ).
2. Рассчитайте дельту Ct для каждого образца
Следующим шагом является расчет дельта Ct ( ∆Ct ) для каждого образца с использованием вновь созданных средних значений Ct. Формула для расчета дельта Ct представлена ниже.
∆Ct = Ct (исследуемый ген) – Ct (ген домашнего хозяйства)
Например, чтобы вычислить ∆Ct для образца ' Control 1 ':
2
∆ 30,55 – 17,18
3.
 Выберите образец(ы) калибратора/эталона для расчета дельты дельты Ct
Выберите образец(ы) калибратора/эталона для расчета дельты дельты CtСледующий шаг – решить, какой образец или группу образцов использовать в качестве калибратора/эталона при расчете дельты -дельта Ct ( ∆∆Ct ) значения для всех образцов. Это часть, которая смущает многих людей. По сути, все зависит от вашей экспериментальной установки.
Обычный способ сделать это - просто сопоставить экспериментальные образцы и отдельно определить относительные коэффициенты экспрессии генов. Все это хорошо и справедливо для экспериментов с соответствующими парами, как, например, в экспериментах с клеточными культурами. Однако это сложно, когда две экспериментальные группы различаются по n числам и не имеют совпадающих пар.
Еще один способ выбора образца для калибровки/эталона — выбрать образец с самым высоким значением Ct, т. е. образец с самой низкой экспрессией гена. Таким образом, все результаты будут относиться к этому образцу. Или вы можете просто выбрать только один из контрольных образцов в качестве эталонного.
Я лично усредняю значения «Среднего Ct» биологических повторов контрольной группы, чтобы создать «Среднее значение контрольного показателя» . Это будет означать, что результаты представлены относительно контрольных средних значений Ct.
Какой бы образец или группу образцов вы ни использовали в качестве калибратора/эталона, это нормально, если это последовательно во всех анализах и сообщается в результатах так, чтобы это было ясно. Помните, что результаты, полученные в конце, равны относительно значений экспрессии генов.
Имея это в виду, если мы хотим получить значений ∆∆Ct для каждого образца (в том числе для каждого контрольного образца), нам сначала нужно усреднить ∆Ct для 3 контрольных образцов:
∆Ct Контрольное среднее = (13,38 + 13,60 + 13,68)/3
Обратите внимание: если значения Ct являются переменными, то может быть более подходящим использовать среднее геометрическое вместо среднего арифметического, указанного выше. Среднее геометрическое более устойчиво к выбросам по сравнению со средним арифметическим. По этой причине среднее геометрическое используется в методе относительной экспрессии генов Vandesompele.
Среднее геометрическое более устойчиво к выбросам по сравнению со средним арифметическим. По этой причине среднее геометрическое используется в методе относительной экспрессии генов Vandesompele.
Например, если значения Ct для моих трех контрольных образцов вместо этого были 13,38, 13,60 и 15,80, то это хорошая причина использовать среднее геометрическое, а не среднее арифметическое.
Чтобы использовать среднее геометрическое, сначала перемножьте числа, а затем извлеките корень n-й степени из этого значения. n — это просто количество наблюдений в формуле, которое в данном примере равно 3. Итак, используя мой последний пример, это будет:
∆Ct Контрольное среднее геометрическое = ∛(13,38 x 13,60 x 15,80)
4. Рассчитайте значения дельта дельта Ct для каждого образца
Теперь рассчитайте значения ∆∆Ct для каждого образца. Помните, что значения дельта дельта Ct в этом примере относятся к необработанной/контрольной группе.

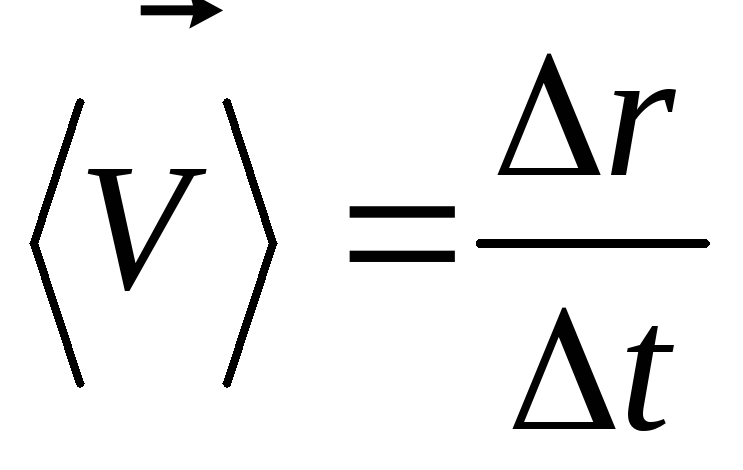 packages("msm")
> библиотека (мсм)
> se_odds_delta=deltamethod(g=~x1/(1-x1), mean=survival_odds, cov=var_p_survival)
> распечатать (se_odds_delta)
[1] 0,1146005
>
packages("msm")
> библиотека (мсм)
> se_odds_delta=deltamethod(g=~x1/(1-x1), mean=survival_odds, cov=var_p_survival)
> распечатать (se_odds_delta)
[1] 0,1146005
> 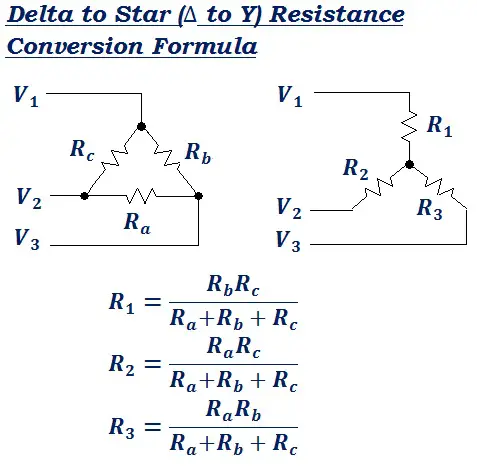 236876e-05 8.216269e-03
> model_beta$se_OR_delta[1]=deltamethod(~exp(x1), mean=model_beta$b[1], cov=vc[1,1])
> model_beta$se_OR_delta[2]=deltamethod(~exp(x1), mean=model_beta$b[2], cov=vc[2,2])
> печать (модель_бета)
b se_b ИЛИ se_OR se_OR_delta
Возраст -0,0087
236876e-05 8.216269e-03
> model_beta$se_OR_delta[1]=deltamethod(~exp(x1), mean=model_beta$b[1], cov=vc[1,1])
> model_beta$se_OR_delta[2]=deltamethod(~exp(x1), mean=model_beta$b[2], cov=vc[2,2])
> печать (модель_бета)
b se_b ИЛИ se_OR se_OR_delta
Возраст -0,0087